Las parábolas son secciones cónicas que son obtenidas en la intersección de un plano con un cono. El plano tiene que cortar a la base del cono para que la parábola sea formada. La característica principal de las parábolas es que todos los puntos en su curva están ubicados a la misma distancia de un punto fijo y de una línea recta. El punto fijo es el foco y la línea recta es la directriz.
A continuación, conoceremos una definición más detallada de las parábolas junto con un diagrama para ilustrarla. Luego, conoceremos las características más importantes de estas secciones cónicas.
PRECÁLCULO
Relevante para…
Aprender sobre las características más importantes de las parábolas.
PRECÁLCULO
Relevante para…
Aprender sobre las características más importantes de las parábolas.
Definición de una parábola
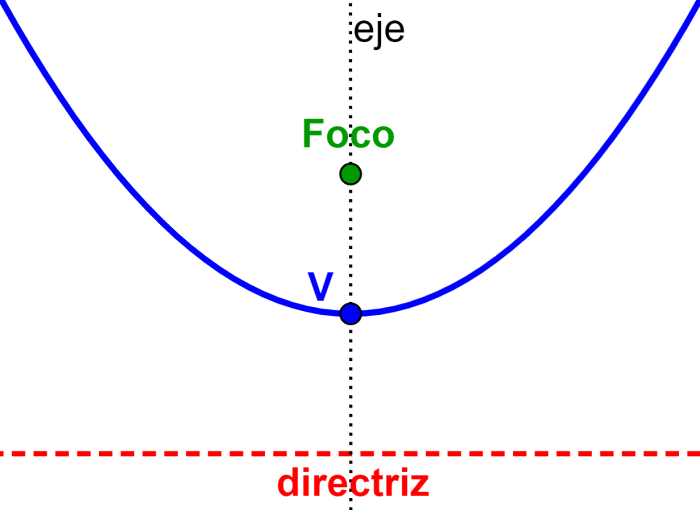
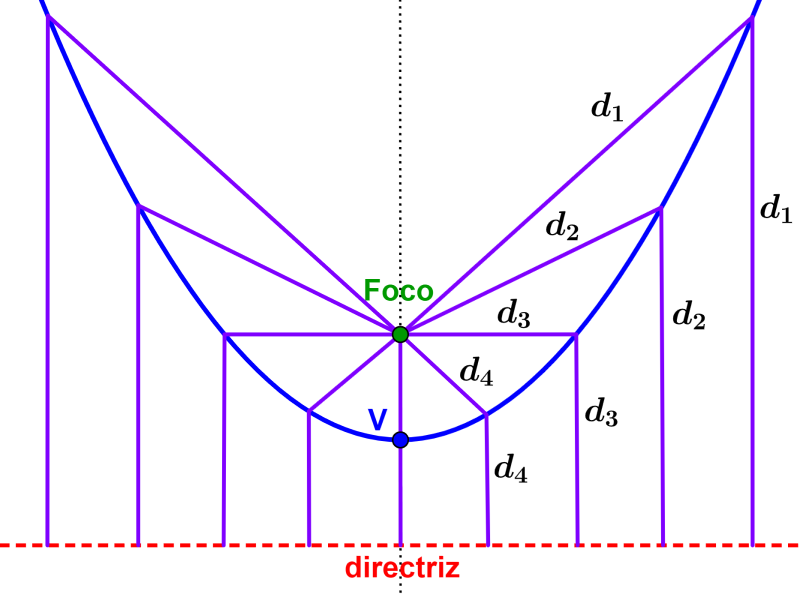
Una parábola está definida como el conjunto de puntos que tienen la misma distancia desde un punto fijo, llamado el foco, y una línea recta, llamada la directriz. En la siguiente imagen, tenemos a una parábola junto con su foco y su directriz. Podemos ver que cada punto en la parábola tiene la misma distancia con respecto al foco y la directriz.
Las parábolas también son definidas como secciones cónicas formadas cuando un plano interseca con un cono. La parábola es formada cuando el plano corta a la cara del cono y tiene un ángulo con respecto al eje de simetría del cono.
El punto de intersección del eje de simetría y la parábola es el vértice. El vértice es el punto extremo de la parábola. Si es que la parábola se abre hacia arriba, el vértice es el punto más bajo y si es que la parábola se abre hacia abajo, el vértice es el punto más alto.
Características principales de una parábola
Las características principales de una parábola son:
- El foco de la parábola siempre está ubicado en la parte interna de la curva.
- La directriz siempre está ubicada en la parte externa de la curva.
- La distancia desde cualquier punto en la parábola es la misma que la distancia desde ese mismo punto hasta la directriz.
- El vértice es el punto extremo de la parábola. Puede ser el punto más bajo o más alto de la parábola.
- La distancia desde el vértice hasta el foco es la misma que la distancia desde el vértice hasta la directriz.
- El eje de simetría cruza a través el vértice.
Ecuación de la parábola
La ecuación de la parábola puede variar dependiendo en si la parábola está centrada en el origen o centrada fuera del origen. Además, también podemos obtener diferentes variaciones de la parábola dependiendo en si está orientada horizontalmente o verticalmente.
- Si es que la parábola está centrada en el origen y está orientada verticalmente, su ecuación es $latex {{x}^2}=4ay$, en donde, a es la distancia desde el vértice hasta el foco.
- Cuando la parábola está centrada en el origen y está orientada horizontalmente, su ecuación es $latex {{y}^2}=4ax$.
- Si es que la parábola está centrada fuera del origen y está orientada verticalmente, su ecuación es $latex {{(x-h)}^2}=4a(y-k)$, en donde, $latex (h, k)$ son las coordenadas del vértice de la parábola.
- Cuando la parábola está centrada fuera del origen y está orientada horizontalmente, su ecuación es $latex {{(y-k)}^2}=4a(x-h)$.
Véase también
¿Interesado en aprender más sobre parábolas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
