El área de un trapecio es la región cubierta por el trapecio en un plano bidimensional. Un trapecio es una figura 2D que está dentro de la categoria de cuadriláteros. En un trapecio, un par de lados es paralelo y el otro par de lados no es paralelo. Similar a otras figuras geométricas, el trapecio también tiene sus propias propiedades y fórmulas basadas en el área y perímetro.
A continuación, conoceremos la fórmula del área de un trapecio. También, veremos algunos ejercicios en los que aplicaremos esta fórmula para encontrar el área.
Fórmula del área de un trapecio
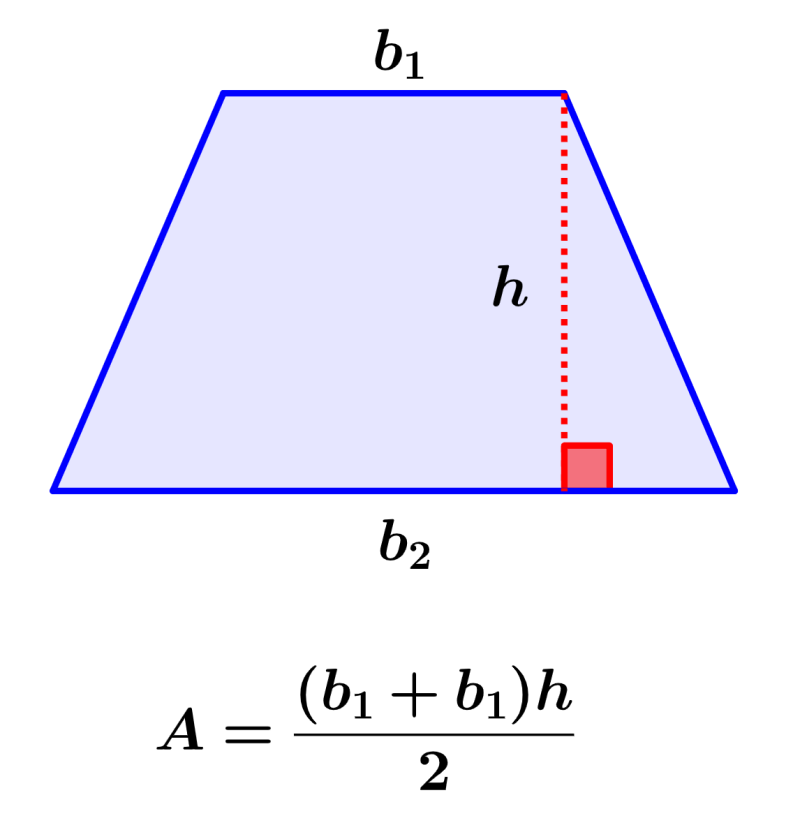
Para encontrar el área de un trapecio, calculamos la suma de sus bases, multiplicamos a esa suma por la altura del trapecio y luego dividimos el resultado por 2. La fórmula para el área del trapecio es:
| $latex A=\frac{(b_{1}+b_{2})h}{2}$ |
en donde,
- $latex b_{1}=$ la longitud de la base 1 del trapecio
- $latex b_{2}=$ la longitud de la base 2 del trapecio
- $latex h=$ la longitud de la altura del trapecio
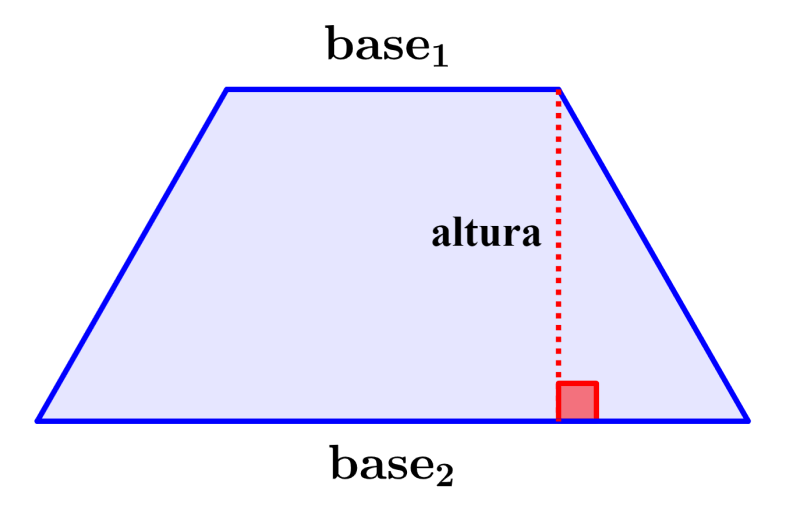
Cada base del trapecio debe ser perpendicular a la altura. En la figura, podemos ver que ambas bases son lados del trapecio. Sin embargo, dado que los lados laterales no son perpendiculares a ninguna de las bases, una línea entrecortada es trazada para representar a la altura.
Derivación de la fórmula del área de un trapecio
Usemos la siguiente figura para derivar la fórmula del área de un trapecio:
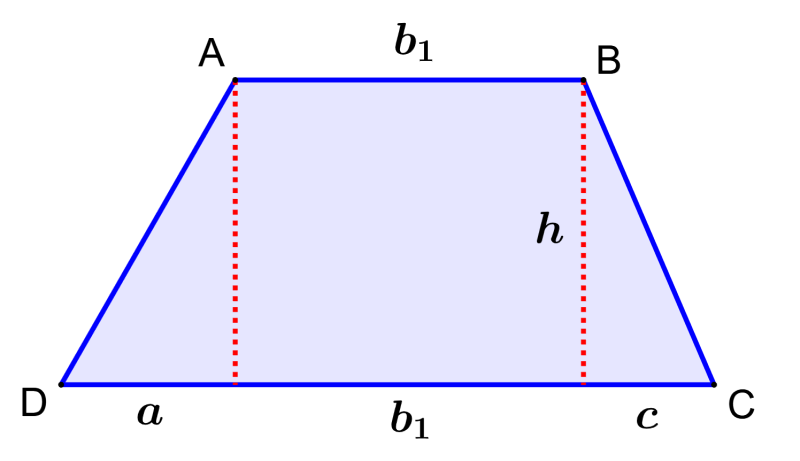
El área de un trapecio es igual a la suma de las áreas de los dos triángulos y el área del rectángulo. Entonces, sabemos que:
área de trapecio = área de triángulo 1 + área de rectángulo + área de triángulo 2
$latex A=\frac{ah}{2}+b_{1}h+\frac{ch}{2}$
$latex A=\frac{ah+2b_{1}h+ch}{2}$
Podemos simplificar la expresión y reorganizar los términos para obtener:
$latex A=\frac{h}{2}(b_{1}+(a+b_{1}+c))$
Si es que usamos $latex b_{2}$ para representar a la base más larga del trapecio, tenemos:
$latex b_{2}=a+b_{1}+c$
Sustituyendo esto en la anterior ecuación, tenemos:
$latex A=\frac{h}{2}(b_{1}+b_{2})$
Entonces, el área del trapecio con bases $latex b_{1}, ~b_{2}$ y altura $latex h$ es $latex A=\frac{h}{2}(b_{1}+b_{2})$.
Ejercicios de área de un trapecio resueltos
Los siguientes ejercicios pueden ser usados para practicar la aplicación de la fórmula del área de un trapecio. Intenta resolver los ejercicios tú mismo antes de mirar el resultado.
EJERCICIO 1
Encuentra el área de un trapecio que tiene bases de longitud 8 m y 12 m y una altura de 10 m.
Solución
Tenemos los siguientes datos:
- Base 1, $latex b_{1}=8$ m
- Base 2, $latex b_{2}=12$ m
- Altura, $latex h=10$ m
Entonces, usamos la fórmula del área reemplazando los datos dados:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(8+12)10}{2}$
$latex =\frac{(20)(10)}{2}$
$latex =\frac{200}{2}$
$latex A=100$
El área del trapecio es 100 m².
EJERCICIO 2
¿Cuál es el área de un trapecio que tiene bases de longitud 11 m y 15 m y una altura de 12 m?
Solución
La pregunta nos da la siguiente información:
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=15$ m
- Altura, $latex h=12$ m
Usando la información dada, tenemos:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(11+15)12}{2}$
$latex =\frac{(26)(12)}{2}$
$latex =\frac{312}{2}$
$latex A=156$
El área del trapecio es 156 m².
EJERCICIO 3
Un trapecio tiene un área de 200 cm², una base de longitud 9 cm y la otra base de longitud 11 cm. ¿Cuál es la altura del trapecio?
Solución
Tenemos la siguiente información:
- Área, $latex A=200$ cm²
- Base 1, $latex b_{1}=9$ cm
- Base 2, $latex b_{2}=11$ cm
Para encontrar la altura, usamos la fórmula del área y despejamos para h:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex 200=\frac{(9+11)h}{2}$
$latex 400=(9+11)h$
$latex 400=20h$
$latex h=20$
La altura del trapecio mide 20 cm.
EJERCICIO 4
Un trapecio tiene un área de 240 m², una base de longitud 11 m y la otra base de longitud 13 m. ¿Cuál es la altura del trapecio?
Solución
De la pregunta, podemos sacar los siguientes valores:
- Área, $latex A=240$ m²
- Base 1, $latex b_{1}=11$ m
- Base 2, $latex b_{2}=13$ m
Usamos la fórmula con los valores dados y despejamos para h:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex 240=\frac{(11+13)h}{2}$
$latex 480=(11+13)h$
$latex 480=24h$
$latex h=20$
La altura del trapecio mide 20 m.
EJERCICIO 5
Calcula el área del siguiente trapecio:
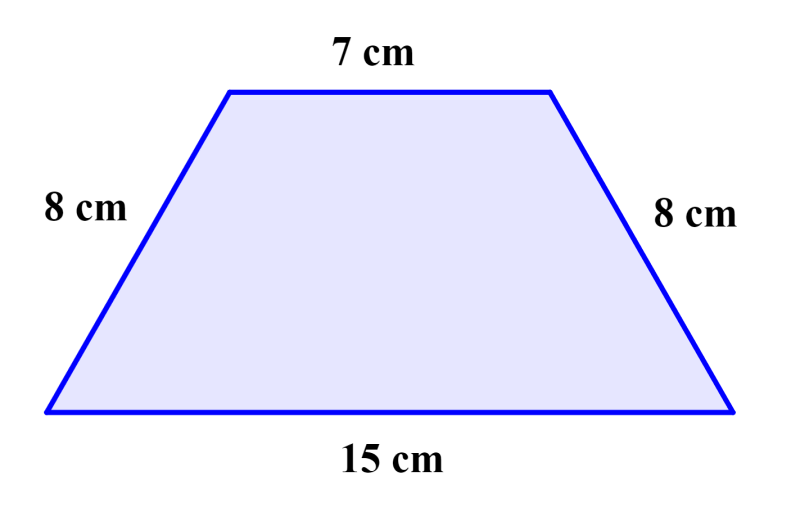
Solución
Dado que los lados no paralelos del trapecio son iguales, la altura puede ser calculada de la siguiente manera:
Obtenemos las bases de los dos triángulos al restar 7 de 15 y dividir para 2.
⇒ $latex \frac{15-7}{2}=4$ cm
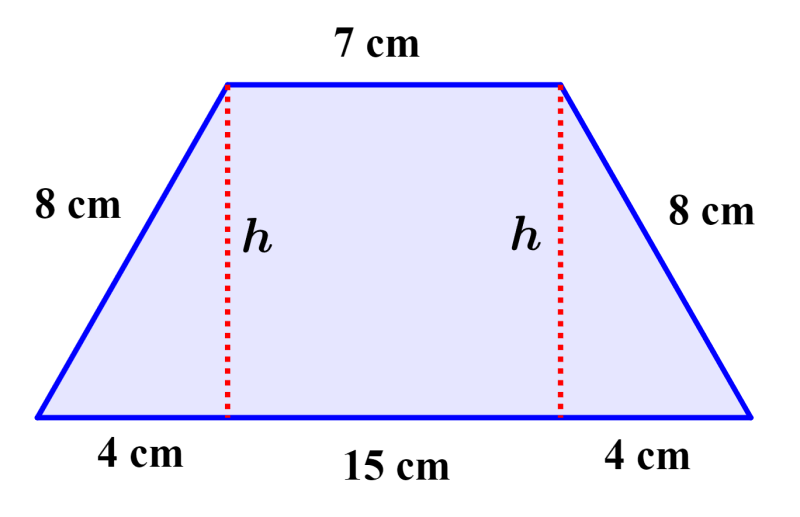
Ahora, podemos usar el teorema de pitágoras para calcular la altura. Entonces, tenemos:
$latex {{8}^2}={{h}^2}+{{4}^2}$
$latex 64={{h}^2}+16$
$latex {{h}^2}=48$
$latex h=6.93$ cm
La altura del trapecio es 6.93 cm. Ahora, calculamos el área con estos valores:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(15+7)6.93}{2}$
$latex =\frac{(22)(6.93)}{2}$
$latex A=76.23$
El área del trapecio es 76.23 cm².
Ejercicios de área de un trapecio para resolver
Pon en práctica lo aprendido sobre el área de un trapecio para resolver los siguientes ejercicios. Selecciona una respuesta y verifícala para comprobar que seleccionaste la correcta.
Véase también
¿Interesado en aprender más sobre trapecios? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
