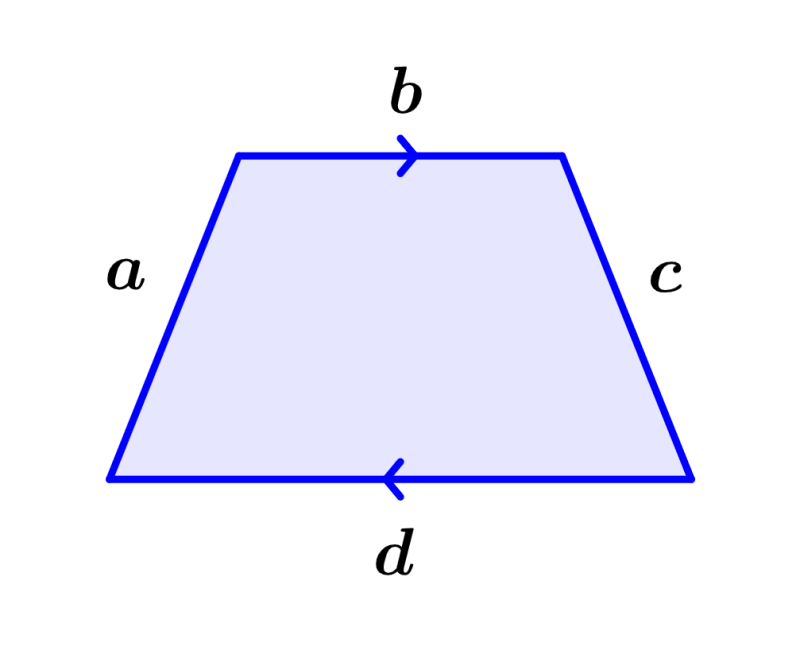
Un trapecio es un cuadrilátero con un par de lados paralelos. Un paralelogramo también puede ser llamado un trapecio, ya que tiene dos lados paralelos. El par de lados paralelos son llamados bases, mientras que los lados no paralelos son llamados lados laterales. Un trapecio isósceles es un trapecio que tiene lados laterales con la misma longitud. Dependiendo en si el trapecio es isósceles o no, puede tener diferentes propiedades.
A continuación, veremos las propiedades fundamentales de los trapecios “normales” y de los trapecios isósceles. Además, veremos sus fórmulas más importantes junto con algunos ejemplos.
Propiedades fundamentales de los trapecios
Las propiedades fundamentales del trapecio son:
- Un par de lados opuestos son paralelos.
- Dos pares de ángulos adyacentes suman 180 grados.
- Los dos lados no-paralelos son desiguales.
- Las diagonales se intersecan.
- La línea que une a los puntos medios de los lados no-paralelos es paralela a los lados paralelos y es igual a la mitad de la suma de ambos lados paralelos.
- Un trapecio puede ser inscrito en un círculo.
- La suma de los cuatro ángulos exteriores es 4 ángulos rectos.
- La suma de los cuatro ángulos interiores es 4 ángulos rectos.
Las propiedades fundamentales del trapecio isósceles son:
- Dos ángulos adyacentes suman 180 grados.
- Cuando los dos lados no-paralelos son iguales y dos pares de ángulos adyacentes son iguales, es llamado un trapecio isósceles.
- Un trapecio isósceles puede ser inscrito en un círculo.
- Las diagonales de un trapecio isósceles son iguales.
- Las diagonales de un trapecio isósceles forman un par de triángulos congruentes con los lados iguales como la base.
- Los dos lados no-paralelos son iguales.
- La línea que une a los puntos medios de los lados no-paralelos es paralela a los lados paralelos y es igual a la mitad de la suma de esos lados.
- La suma de los cuatro ángulos exteriores es 4 ángulos rectos.
- La suma de los cuatro ángulos interiores es 4 ángulos rectos.
- Al rotar al trapecio isósceles con respecto al lado paralelo más corto, obtenemos conos cóncavos en ambos extremos.
- Al rotar al trapecio isósceles con respecto al lado paralelo más largo, obtenemos conos convexos en ambos extremos.
Fórmulas importantes de los trapecios
Las siguientes fórmulas son las más importantes para resolver problemas relacionados con trapecios.
Área de un trapecio: El área de un trapecio puede ser calculada usando la longitud de sus bases (lados paralelos) y la longitud de su altura, la cual es la distancia perpendicular entre los lados paralelos. La fórmula para el área de un trapecio es:
| $latex A=\frac{(b_{1}+b_{2})h}{2}$ |
en donde,
- $latex b_{1}$ es la longitud de uno de los lados paralelos del trapecio
- $latex b_{2}$ es la longitud del otro lado paralelo del trapecio
- $latex h$ es la longitud la altura del trapecio
Perímetro del trapecio: El perímetro del trapecio es calculado al sumar las longitudes de todos los lados. Entonces, tenemos la fórmula:
| $latex A=a+b+c+d$ |
en donde,
- $latex a, b, c, d$ representan a las longitudes de los cuatro lados del trapecio
Ejemplos de problemas de trapecios
EJEMPLO 1
¿Cuál es el área de un trapecio que tiene lados paralelos de longitud 14 m y 16 m y una altura de 10 m?
Solución: Tenemos la siguiente información:
- Base 1, $latex b_{1}=14$ m
- Base 2, $latex b_{2}=16$ m
- Altura, $latex h=10$ m
Entonces, reemplazando estos valores en la fórmula del área, tenemos:
$latex A=\frac{(b_{1}+b_{2})h}{2}$
$latex =\frac{(14+16)10}{2}$
$latex =\frac{(30)10}{2}$
$latex =\frac{300}{2}$
$latex A=150$
El área del trapecio es 150 m².
EJEMPLO 2
¿Cuál es el perímetro de un trapecio que tiene lados de longitud 9 m, 15 m, 13 m y 12 m?
Solución: Tenemos la siguiente información:
- Lado 1, $latex a=9$ m
- Lado 2, $latex b=15$ m
- Lado 3, $latex c=13$ m
- Lado 4, $latex d=12$ m
Entonces, reemplazando estos valores en la fórmula del perímetro, tenemos:
$latex p=a+b+c+d$
$latex =9+15+13+12$
$latex p=49$
El perímetro del trapecio es 49 m.
Véase también
¿Interesado en aprender más sobre trapecios? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
