La apotema de cualquier polígono es igual a la línea que conecta al centro del polígono con uno de sus lados en forma perpendicular. Usando la apotema, podemos calcular el área de los polígonos de una manera más fácil. Podemos encontrar una fórmula para la apotema de un octágono al dividir al octágono en ocho triángulos congruentes y usar trigonometría para determinar la altura de uno de los triángulos, ya que es equivalente a la apotema.
A continuación, derivaremos una fórmula para la apotema de octágonos usando trigonometría. Además, aplicaremos esta fórmula para resolver algunos ejercicios.
Fórmula de la apotema de un octágono
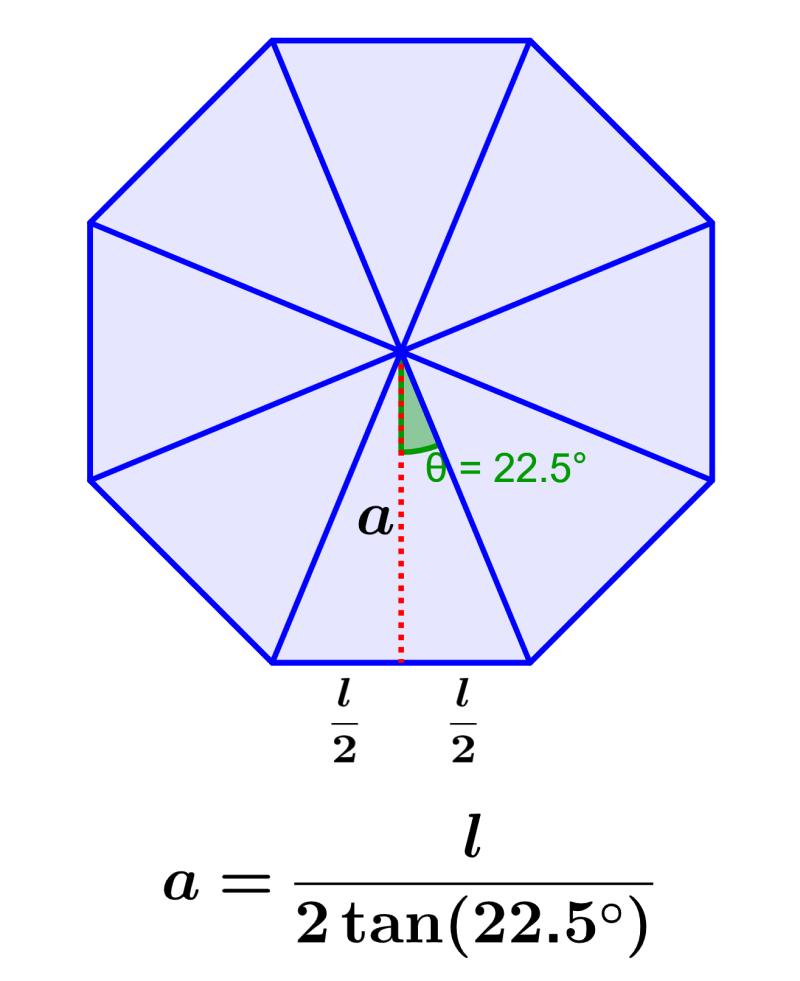
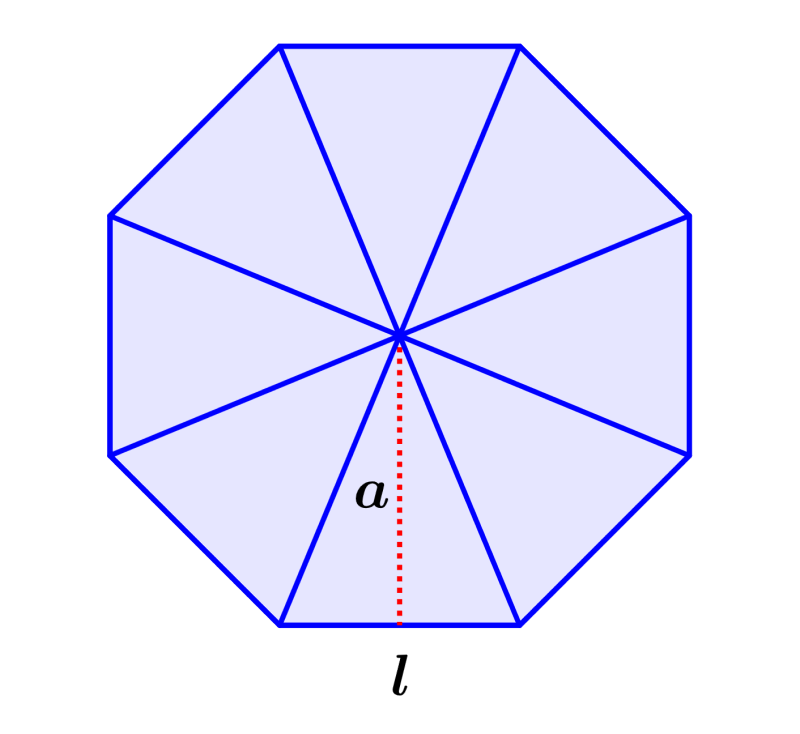
Podemos encontrar una fórmula para la apotema de un octágono usando trigonometría. Para esto, empezamos dividiendo al octágono en ocho triángulos congruentes:
Vemos que la apotema divide al triángulo en dos triángulos rectángulos pequeños. Podemos ver que la altura del triángulo es igual a la apotema, por lo que podemos encontrar una expresión para la apotema usando trigonometría. Tenemos que encontrar la medida del ángulo central de uno de los triángulos rectángulos.
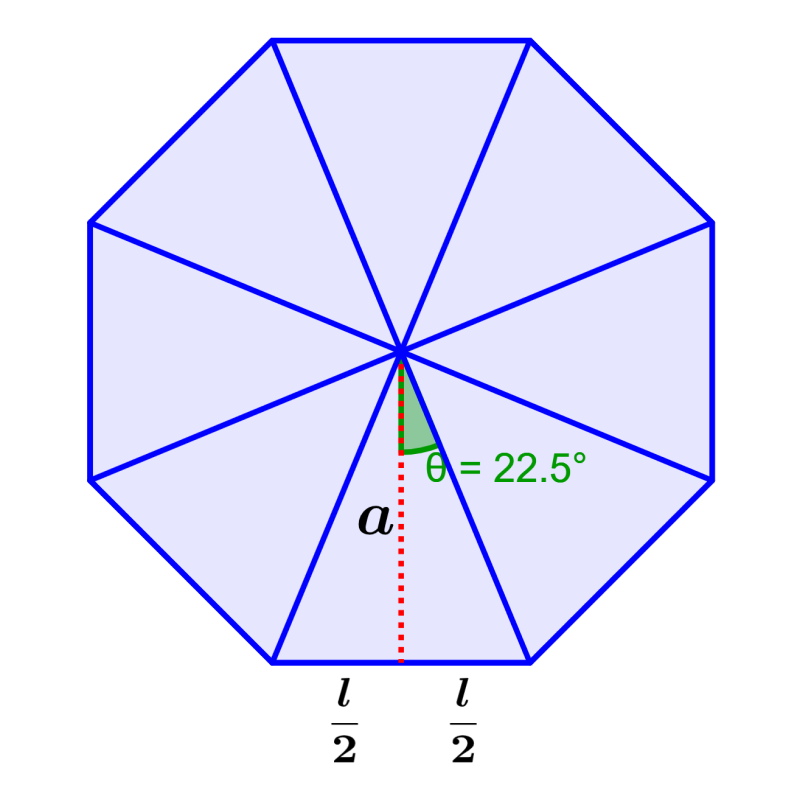
Sabemos que el ángulo central del octágono es igual a 360°. Además, sabemos que tenemos 16 triángulos rectángulos pequeños, por lo que el ángulo central de cada uno es $latex 360\div 16=22.5$°:
Ahora que tenemos el ángulo, podemos usar la función tangente, la cual nos dice que la tangente del ángulo es igual al lado opuesto sobre el lado adyacente. Entonces, tenemos:
$latex \tan(22.5)=\frac{\text{opuesto}}{\text{adyacente}}$
$latex \tan(22.5)=\frac{\frac{l}{2}}{a}$
$latex \tan(22.5)=\frac{l}{2a}$
| $latex a=\frac{l}{2tan(22.5)}$ |
Ejercicios de apotema de octágonos resueltos
La fórmula de la apotema de octágonos es usada para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo primero.
EJERCICIO 1
Un octágono tiene lados de longitud 4 m. ¿Cuál es su apotema?
Solución
Usando la fórmula de la apotema con la longitud $latex l=4$, tenemos:
$latex a=\frac{l}{2\tan(22.5°)}$
$latex a=\frac{4}{2\tan(22.5°)}$
$latex a=\frac{4}{0.828}$
$latex a=4.83$
La longitud de la apotema es 4.83 m.
EJERCICIO 2
¿Cuál es la longitud de la apotema de un octágono que tiene lados de longitud 5 m?
Solución
En este caso, tenemos la longitud $latex l=5$, por lo que usamos la fórmula con este valor:
$latex a=\frac{l}{2\tan(22.5°)}$
$latex a=\frac{5}{2\tan(22.5°)}$
$latex a=\frac{5}{0.828}$
$latex a=6.04$
La longitud de la apotema es 6.04 m.
EJERCICIO 3
Un octágono tiene lados de longitud 9 m. ¿Cuál es su apotema?
Solución
Podemos usar la fórmula de la apotema con la longitud $latex l=9$. Entonces, tenemos:
$latex a=\frac{l}{2\tan(22.5°)}$
$latex a=\frac{9}{2\tan(22.5°)}$
$latex a=\frac{9}{0.828}$
$latex a=10.87$
La longitud de la apotema es 10.87 m.
EJERCICIO 4
Un octágono tiene una apotema de longitud 11.5 m. ¿Cuál es la longitud de sus lados?
Solución
Aquí, empezamos con la longitud de la apotema y queremos encontrar la longitud de los lados. Entonces, usamos la fórmula de la apotema con $latex a=11.5$ y resolvemos para l:
$latex a=\frac{l}{2\tan(22.5°)}$
$latex 11.5=\frac{l}{2\tan(22.5°)}$
$latex 11.5=\frac{l}{0.828}$
$latex l=11.5(0.828)$
$latex l=9.52$
La longitud de los lados del octágono es 9.52 m.
EJERCICIO 5
¿Cuál es la longitud de los lados de un octágono que tiene una apotema de longitud 15 m?
Solución
Nuevamente, usamos la fórmula de la apotema con $latex a=15$ y resolvemos para l:
$latex a=\frac{l}{2\tan(22.5°)}$
$latex 15=\frac{l}{2\tan(22.5°)}$
$latex 15=\frac{l}{0.828}$
$latex l=15(0.828)$
$latex l=12.42$
La longitud de los lados del octágono es 12.42 m.
Ejercicios de apotema de octágonos para resolver
Pon en práctica el uso de la fórmula de la apotema para resolver los siguientes ejercicios. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre octágonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
