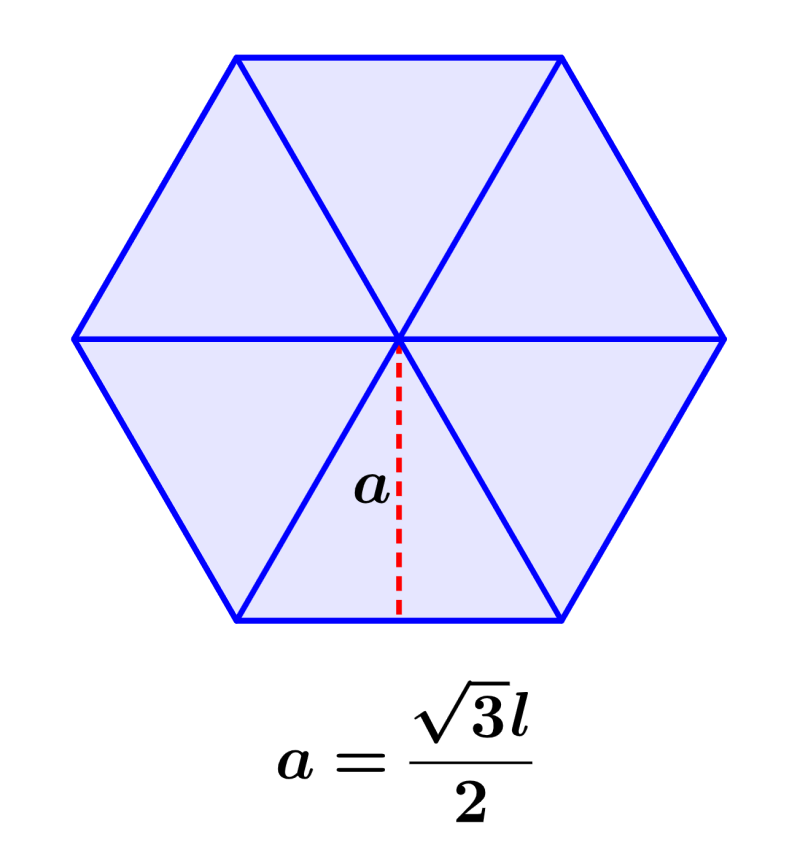
La apotema de un hexágono es la longitud de la línea que une al centro del hexágono con el centro de un lado. La apotema es la línea perpendicular que conecta al centro del hexágono con un lado. La apotema puede ser muy útil cuando queremos encontrar el área de un hexágono, ya que nos permite utilizar una fórmula más simple. Podemos calcular la apotema al dividir al hexágono en seis triángulos congruentes y usar uno de los triángulos. Podemos usar el teorema de Pitágoras o trigonometría para derivar fórmulas diferentes.
A continuación, conoceremos las fórmulas de la apotema de un hexágono. Además, resolveremos algunos ejercicios usando estas fórmulas.
GEOMETRÍA
Relevante para…
Aprender a calcular la apotema de un hexágono con ejercicios.
GEOMETRÍA
Relevante para…
Aprender a calcular la apotema de un hexágono con ejercicios.
Fórmula de la apotema de un hexágono
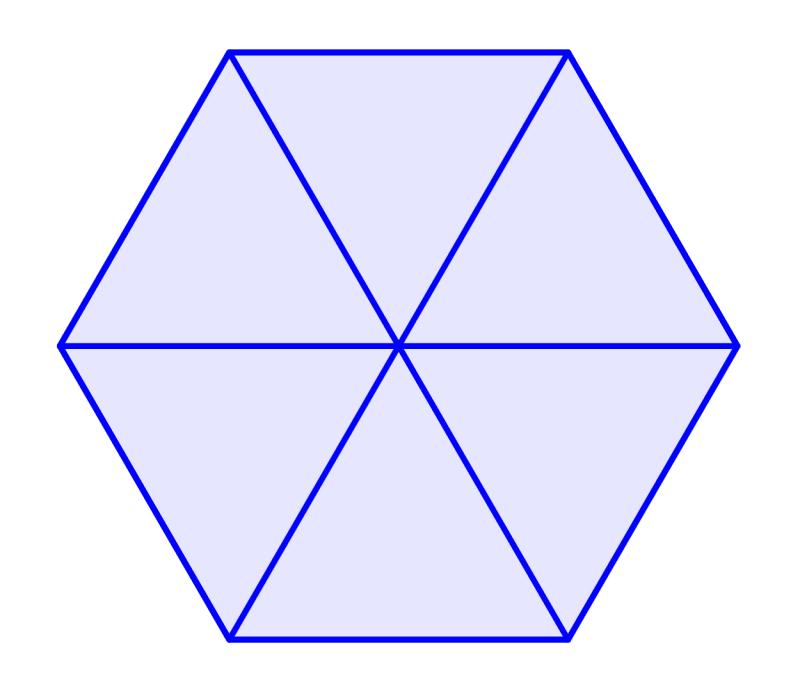
Existen dos métodos principales que podemos usar para derivar una fórmula para la apotema de hexágonos. Ambos métodos involucran dividir al hexágono en seis triángulos congruentes como en la siguiente imagen:
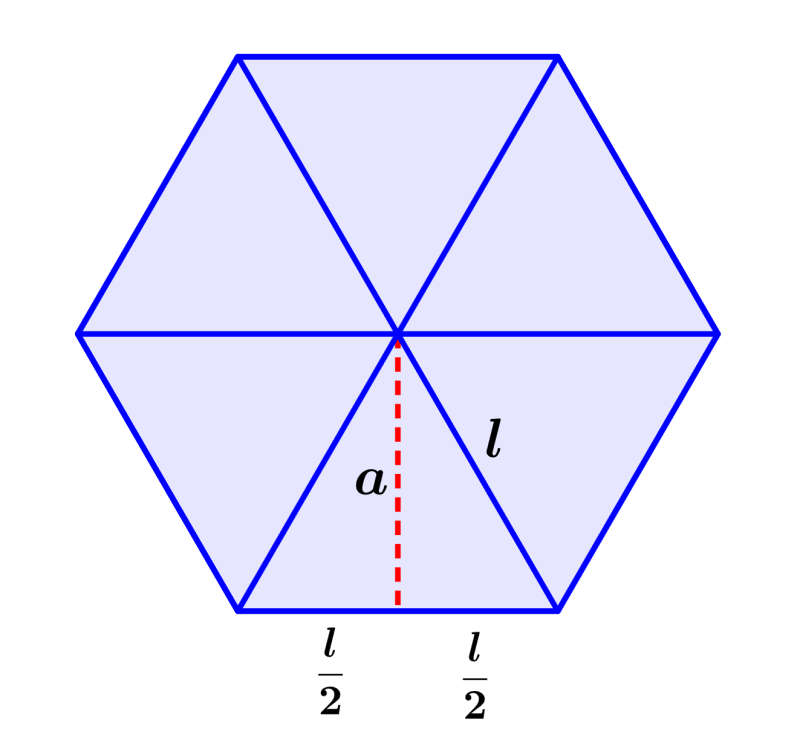
Primer método: Podemos usar el teorema de Pitágoras en uno de los triángulos formados. Sabemos que los triángulos formados son equiláteros, por lo que sus tres lados son iguales. Además, trazando la apotema, vemos que divide a la base en dos partes iguales como en la imagen:
Entonces, usando estas longitudes, tenemos:
$latex {{l}^2}={{a}^2}+{{(\frac{l}{2})}^2}$
$latex {{a}^2}={{l}^2}-{{(\frac{l}{2})}^2}$
$latex {{a}^2}={{l}^2}-\frac{{{l}^2}}{4}$
$latex {{a}^2}=\frac{3{{l}^2}}{4}$
| $latex a=\frac{\sqrt{3}l}{2}$ |
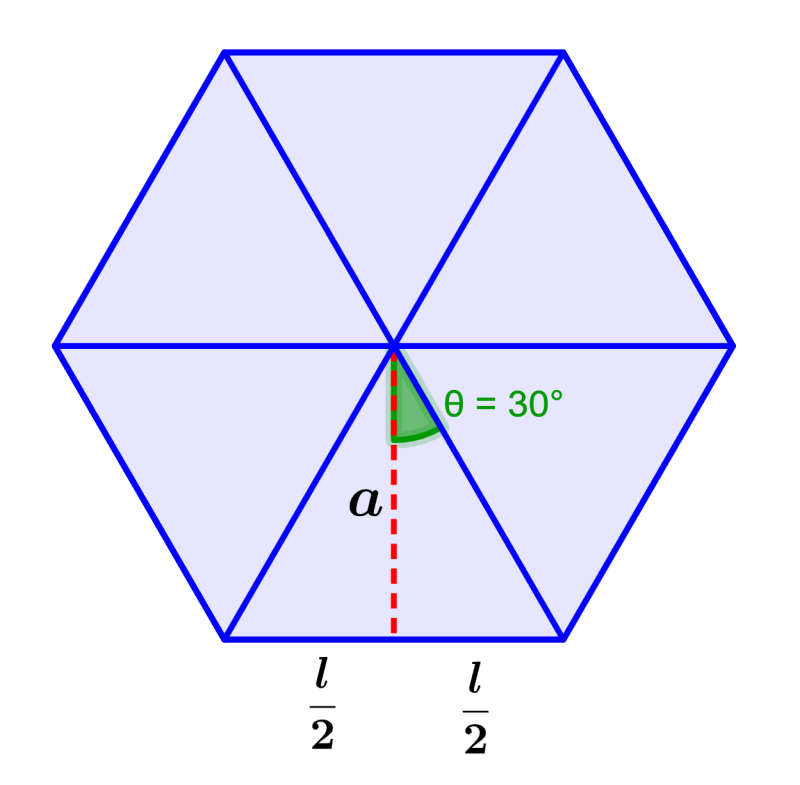
Segundo método: Similar al anterior método, dividimos al hexágono en seis triángulos congruentes. Al trazar la apotema, dividimos al triángulo por la mitad, eso significa que si hiciéramos esto con todos los triángulos, tendríamos 12 triángulos pequeños en total.
Para usar trigonometría, tenemos que encontrar el ángulo central. Dado que el ángulo central total es igual a 360°, el ángulo central de cada triángulo pequeño mide $latex 360\div 12=30$°:
Ahora, podemos usar la tangente. Sabemos que la tangente de un ángulo es igual al lado opuesto sobre lado adyacente:
$latex \tan(30°)=\frac{\text{opuesto}}{\text{adyacente}}$
$latex \tan(30°)=\frac{\frac{l}{2}}{a}$
$latex \tan(30°)=\frac{l}{2a}$
| $latex a=\frac{l}{2\tan(30°)}$ |
Ejercicios de apotema de hexágonos resueltos
Los siguientes ejercicios usan ambas fórmulas de la apotema de hexágonos vistas arriba. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar el resultado.
EJERCICIO 1
¿Cuál es la longitud de la apotema de un hexágono que tiene lados de longitud 6 m?
Solución
Primera fórmula: Usando la primera fórmula con $latex l=6$, tenemos:
$latex a=\frac{\sqrt{3}l}{2}$
$latex a=\frac{\sqrt{3}(6)}{2}$
$latex a=5.2$
La longitud de la apotema es 5.2 m.
Segunda fórmula: Usando la segunda fórmula con $latex l=6$, tenemos:
$latex a=\frac{l}{2\tan(30°)}$
$latex a=\frac{6}{2\tan(30°)}$
$latex a=5.2$
Vemos que obtuvimos el mismo resultado usando ambas fórmulas.
EJERCICIO 2
Un hexágono tiene lados de longitud 8 m. ¿Cuál es la longitud de su apotema?
Solución
Primera fórmula: Podemos usar $latex l=8$ en la primera fórmula:
$latex a=\frac{\sqrt{3}l}{2}$
$latex a=\frac{\sqrt{3}(8)}{2}$
$latex a=6.93$
La longitud de la apotema es 6.93 m.
Segunda fórmula: Si es que ahora usamos la segunda fórmula con $latex l=8$, tenemos:
$latex a=\frac{l}{2\tan(30°)}$
$latex a=\frac{8}{2\tan(30°)}$
$latex a=6.93$
Obtuvimos la misma longitud con ambas fórmulas.
EJERCICIO 3
¿Cuál es la longitud de la apotema de un hexágono con lados de longitud 10 m?
Solución
Primera fórmula: Al usar la primera fórmula con $latex l=10$, tenemos:
$latex a=\frac{\sqrt{3}l}{2}$
$latex a=\frac{\sqrt{3}(10)}{2}$
$latex a=8.66$
La longitud de la apotema es 8.66 m.
Segunda fórmula: Al usar la segunda fórmula con $latex l=10$, tenemos:
$latex a=\frac{l}{2\tan(30°)}$
$latex a=\frac{10}{2\tan(30°)}$
$latex a=8.66$
El mismo resultado fue obtenido con ambas fórmulas.
EJERCICIO 4
¿Cuál es la longitud de los lados de un hexágono que tiene una apotema de 7.5 m?
Solución
En este caso, tenemos la longitud de la apotema y queremos encontrar la longitud de los lados del hexágono.
Primera fórmula: Usamos la primera fórmula con $latex a=7.5$ y resolvemos para l:
$latex a=\frac{\sqrt{3}l}{2}$
$latex 7.5=\frac{\sqrt{3}l}{2}$
$latex 15=\sqrt{3}l$
$latex l=8.66$
La longitud de los lados del hexágono es 8.66 m.
Segunda fórmula: Usamos la segunda fórmula con $latex a=7.5$ y resolvemos para l:
$latex a=\frac{l}{2\tan(30°)}$
$latex 7.5=\frac{l}{2\tan(30°)}$
$latex l=7.5(2\tan(30°))$
$latex l=8.66$
Obtuvimos la misma longitud con ambas fórmulas.
EJERCICIO 5
¿Cuál es la longitud de los lados de un hexágono que tiene una apotema de longitud 12 m?
Solución
Nuevamente, usamos ambas fórmulas y resolvemos para l.
Primera fórmula: Reemplazamos a $latex a=12$ y resolvemos para l:
$latex a=\frac{\sqrt{3}l}{2}$
$latex 12=\frac{\sqrt{3}l}{2}$
$latex 24=\sqrt{3}l$
$latex l=13.87$
La longitud de los lados del hexágono es 13.87 m.
Segunda fórmula: Reemplazamos a $latex a=12$ y resolvemos para l:
$latex a=\frac{l}{2\tan(30°)}$
$latex 12=\frac{l}{2\tan(30°)}$
$latex l=12(2\tan(30°))$
$latex l=13.86$
En este caso, obtuvimos una pequeña diferencia en los decimales. Esto se debe al redondeo usado a la hora de realizar las operaciones.
Ejercicios de apotema de hexágonos para resolver
Practica el uso de las fórmulas de la apotema de hexágonos y resuelve los siguientes ejercicios. Selecciona una respuesta y haz clic en “Verificar” para comprobar tu respuesta. Si necesitas ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre hexágonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
