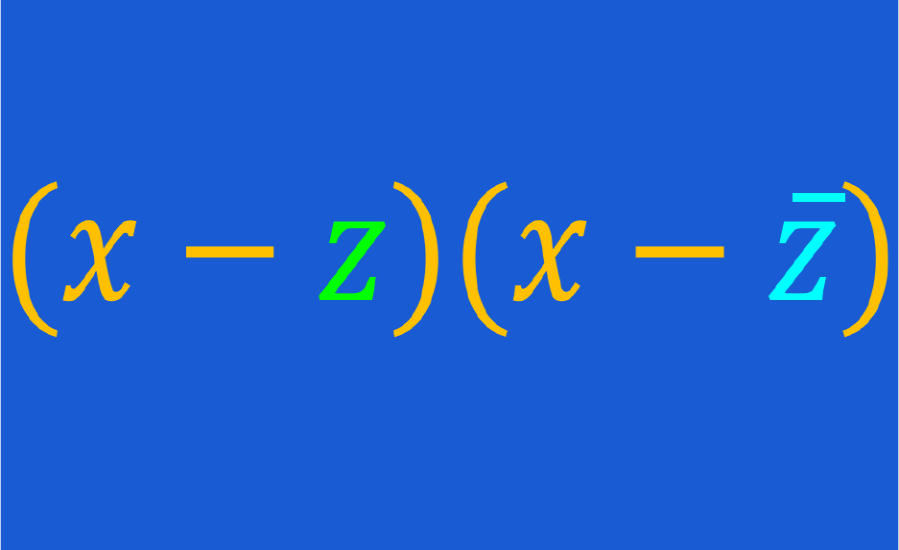Las raíces complejas conjugadas de un polinomio son aquellas raíces complejas que son conjugadas la una de la otra. Recordemos que los conjugados son dos números complejos que tienen la misma parte real y tienen a la parte negativa con un signo diferente la una de la otra.
A continuación, haremos una revisión de los números complejos conjugados. También, conoceremos el teorema de raíces conjugadas de un polinomio. Finalmente, veremos varios ejercicios de raíces complejas conjugadas para mirar la aplicación de este teorema.
¿Qué son los conjugados de números complejos?
Los conjugados complejos son dos números complejos, por lo que tienen la forma $latex a+bi$, en donde, a y b son números reales y $latex i=\sqrt{-1}$. La a es llamada la parte real de un número complejo y la bi es llamada la parte imaginaria.
Dos números complejos son conjugados el uno del otro si es que tienen la misma parte real y las partes imaginarias son negativas la una de la otra. Esto significa que el conjugado del número $latex a+bi$ es $latex a-bi$.
Por ejemplo, si es que tenemos al número complejo $latex 4+5i$, sabemos que su conjugado es $latex 4-5i$. De igual forma, el conjugado complejo de $latex 2-4i$ es $latex 2+4i$. Encontrar el conjugado de un número complejo es muy fácil, simplemente cambiamos el signo de la parte imaginaria del número.
¿Qué son las raíces complejas conjugadas?
Las raíces complejas conjugadas pueden ser descritas usando el teorema de raíces conjugadas:
Teorema de raíces conjugadas
Si es que el número complejo $latex a+bi$ es una raíz del polinomio $latex P(x)$ en una variable con coeficientes reales, entonces, el conjugado complejo $latex a-bi$ también es una raíz de ese polinomio.
Este teorema resulta muy útil para encontrar raíces de polinomios. Por ejemplo, supongamos que estamos intentando encontrar todas las raíces de un polinomio y a medida que vamos resolviendo, encontramos que $latex a+bi$ es una raíz del polinomio.
Sabiendo esto, automáticamente conocemos otra raíz más. Por el teorema de raíces conjugadas, sabemos que si es que $latex a+bi$ es una raíz, entonces, $latex a-bi$ debe ser una raíz.
Por ejemplo, si es que encontramos que $latex 6-3i$ es una raíz de un polinomio, entonces, $latex 6+3i$ también es una raíz de ese polinomio. Este teorema nos ahorra tiempo y esfuerzo al no tener que usar un proceso adicional para encontrar esa raíz.
Ejercicios de raíces complejas conjugadas resueltos
El teorema de raíces complejas conjugadas es usado para resolver los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, pero es recomendable que intentes resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Si es que $latex z=2+3i$ es una raíz de $latex p(z)={{z}^2}-4z+13$, demuestra que $latex {{z}^{\ast}}=2-3i$ es otra raíz.
Solución
Sabemos que si es que z es una raíz de un polinomio, debemos tener $latex p(z)=0$. Entonces, podemos usar $latex z=2-3i$ en el polinomio e igualar con cero para verificar si es que es una raíz:
$$p(2-3i)={{(2-3i)}^2}-4(2-3i)+13$$
$latex =4-12i+9{{i}^2}-8+12i+13$
$latex =9+9(-1)$
$latex =0$
Obtuvimos cero luego de reemplazar a $latex z=2-3i$ en el polinomio. Esto significa que sí es una raíz.
EJERCICIO 2
¿Cuáles son las raíces de $latex 4{{x}^2}+10=-90$?
Solución
Esta ecuación puede ser resuelta directamente al despejar a la variable a un lado de la ecuación.
Restamos 10 a ambos lados y luego dividimos por 4 para despejar a $latex {{x}^2}$:
$latex 4{{x}^2}+10=-90$
$latex 4{{x}^2}=-100$
$latex {{x}^2}=-25$
Ahora, podemos tomar la raíz cuadrada de ambos lados de la ecuación. Usamos el signo $latex \pm$ ya que tenemos una raíz positiva y otra negativa:
$latex x=\pm\sqrt{-25}$
Sabemos que podemos reescribir a $latex \sqrt{-a}$ como $latex i \sqrt{a}$. Entonces, tenemos:
$latex x=\pm i\sqrt{25}$
$latex =\pm 5i$
Entonces, las raíces del polinomio son los conjugados $latex x=5i $ y $latex x=-5i$.
EJERCICIO 3
¿Cuáles son las raíces del polinomio cuadrático $latex {{x}^2}-4x+8=0$?
Solución
En este caso, podemos usar la fórmula cuadrática para resolver:
$latex x=\frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}$
Aquí, tenemos los valores $latex a=1$, $latex b=-4$ y $latex c=8$. Entonces, reemplazando estos valores, tenemos:
$latex x=\frac{{-(-4)\pm \sqrt{{{{{( -4)}}^{2}}-4( 1 )(8)}}}}{{2( 1)}}$
$latex =\frac{{4\pm \sqrt{{16-32}}}}{2}$
$latex =\frac{{4\pm \sqrt{{-16}}}}{2}$
$latex =\frac{4}{2}\pm \frac{\sqrt{{-16}}}{2}$
$latex =2\pm \frac{\sqrt{{-16}}}{2}$
Nuevamente, podemos usar el hecho que $latex \sqrt{-a}=i\sqrt{a}$ para reescribir a la expresión:
$latex x=2\pm \frac{\sqrt{{16}}}{2}i$
$latex =2\pm \frac{4}{2}i$
$latex =2\pm 2i$
Obtuvimos las dos soluciones conjugadas para la ecuación cuadrática:
$latex x=2+2i$, $latex x=2-2i$
EJERCICIO 4
Resuelve la ecuación $latex 3{{x}^2}-4x+10=0$ y encuentra sus raíces.
Solución
Similar al ejercicio anterior, podemos usar la fórmula cuadrática con los valores $latex a=3$, $latex b=-4$ y $latex c=10$. Entonces, tenemos:
$latex x=\frac{{-(-4)\pm \sqrt{{{{{( -4)}}^{2}}-4( 3 )(10)}}}}{{2( 3)}}$
$latex =\frac{{4\pm \sqrt{{16-120}}}}{6}$
$latex =\frac{{4\pm \sqrt{{-104}}}}{6}$
$latex =\frac{{4\pm \sqrt{{-4}}\sqrt{{26}}}}{6}$
$latex =\frac{{4\pm 2i \sqrt{{26}}}}{6}$
$latex =\frac{{2\pm i \sqrt{{26}}}}{3}$
Las soluciones conjugadas de la ecuación cuadrática son:
$latex =\frac{{2+ i \sqrt{{26}}}}{3}$, $latex =\frac{{2- i \sqrt{{26}}}}{3}$
→ Calculadora de Raíces Complejas
Ejercicios de raíces complejas conjugadas para resolver
Pon en práctica lo aprendido sobre las raíces complejas conjugadas para resolver los siguientes ejercicios. Si necesitas ayuda con estos ejercicios, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre polinomios? Mira estas páginas: