La suma de ángulos interiores de un triángulo siempre es igual a 180°. Esto se debe a que, si es que unimos los tres ángulos interiores del triángulo, formaremos una línea recta. Esta propiedad puede ser usada para encontrar las diferentes medidas de los tres ángulos interiores del triángulo.
A continuación, aprenderemos más sobre los ángulos interiores y veremos algunos ejemplos de práctica.
Suma de ángulos interiores de un triángulo
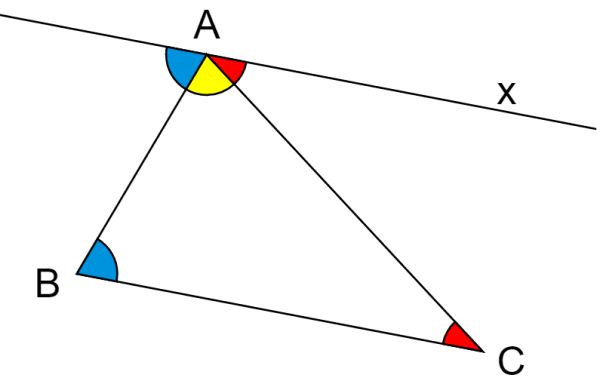
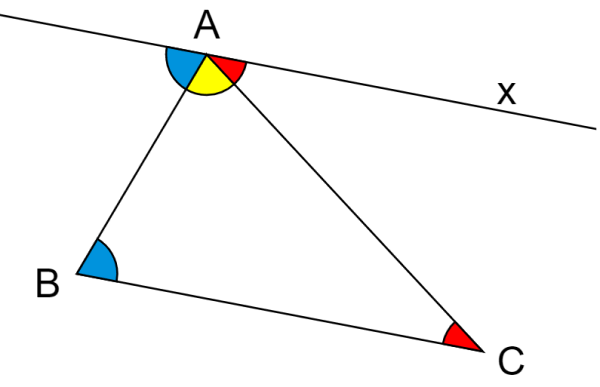
La suma total de los tres ángulos interiores de cualquier triángulo siempre es igual a 180°. Podemos verificar esto usando el siguiente diagrama:
La línea x es paralela a la base del triángulo, es decir, a la línea BC. Sabemos que cuando dos líneas paralelas son intersecadas por una transversal, formamos ángulos correspondientes y ángulos verticales.
Entonces, los ángulos que tienen el mismo color son iguales. Por ejemplo, los ángulos rojos tienen la misma medida.
Cuando unimos a los tres ángulos en el vértice A, podemos ver que forman una línea recta, por lo que su suma total es igual a 180°.
¿Cómo calcular los ángulos interiores individuales de un triángulo?
Las medidas de cada ángulo individual pueden ser calculadas usando el hecho que su suma total es igual a 180°. Además, dependiendo del tipo de triángulo, necesitamos diferente información.
Ángulos interiores de triángulos equiláteros
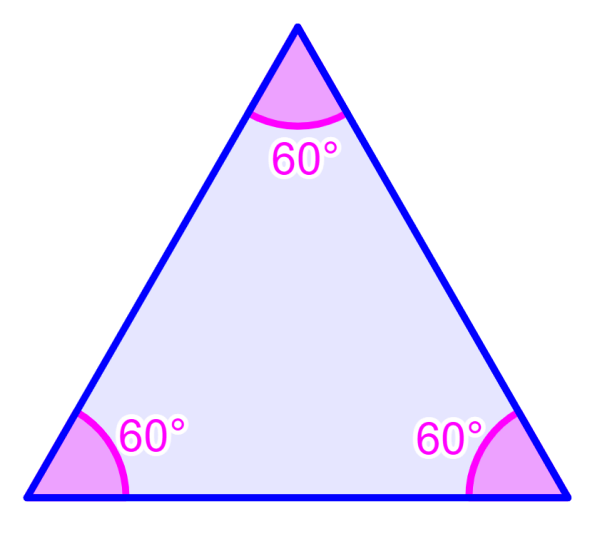
Los triángulos equiláteros son triángulos que se caracterizan por tener todos sus lados iguales. Esto significa que la medida de sus tres ángulos interiores es la misma. Entonces, podemos calcular la medida de un ángulo interior simplemente al dividir la suma total de 180° por 3. Entonces, tenemos:
180°÷3=60°
Cada ángulo interior de cualquier triángulo equilátero siempre mide 60°.
Ángulos interiores de triángulos isósceles
Los triángulos isósceles son triángulos que tienen dos lados con la misma longitud y un tercer lado con una longitud diferente. Estos triángulos también tienen dos ángulos con la misma medida y un tercer ángulo con medida diferente.
Generalmente, los ángulos iguales son representados con doble línea. Entonces, podemos determinar la medida de cada ángulo interior si es que conocemos la medida de un ángulo.
Ángulos interiores de triángulos escalenos
Los triángulos escalenos son triángulos que tienen todos sus lados con longitudes diferentes. Además, los tres ángulos interiores también tienen medidas diferentes. Esto significa que necesitamos las medidas de dos ángulos interiores para calcular la medida del tercer ángulo.
Ejemplos de ángulos interiores de un triángulo
EJEMPLO 1
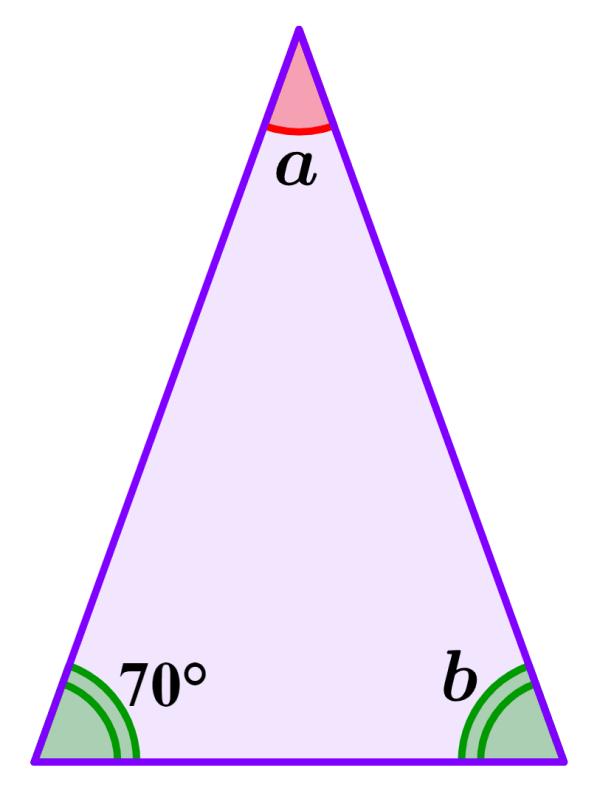
Determina las medidas de los ángulos interiores faltantes del siguiente triángulo isósceles.
Solución: Los ángulos verdes, los cuales están representados con la doble línea, tienen la misma medida. Entonces, tenemos b=70°.
Para encontrar la medida del ángulo a, sumamos las medidas de los ángulos conocidos y restamos de 180°. Entonces, tenemos:
70°+70°=140°
⇒ 180°-140°=40°
El ángulo a mide 40°.
EJEMPLO 2
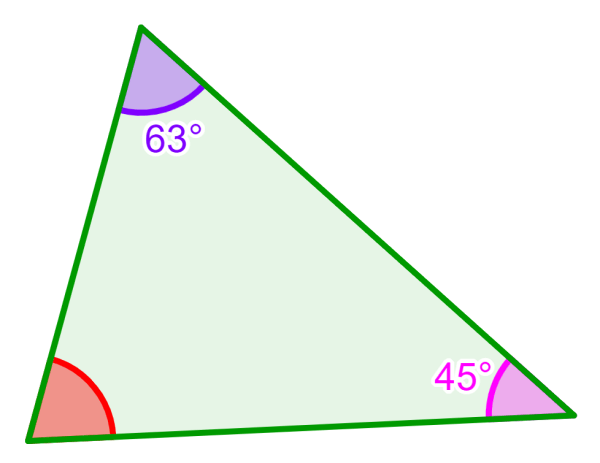
¿Cuál es la medida del ángulo faltante en el siguiente triángulo escaleno?
Solución: Un triángulo escaleno tiene tres ángulos con medidas diferentes. Entonces, encontramos la medida del tercer ángulo al sumar los ángulos conocidos y restar de 180°:
63°+45°=108°
⇒ 180°-108°=72°
El ángulo faltante mide 72°.
EJEMPLO 3
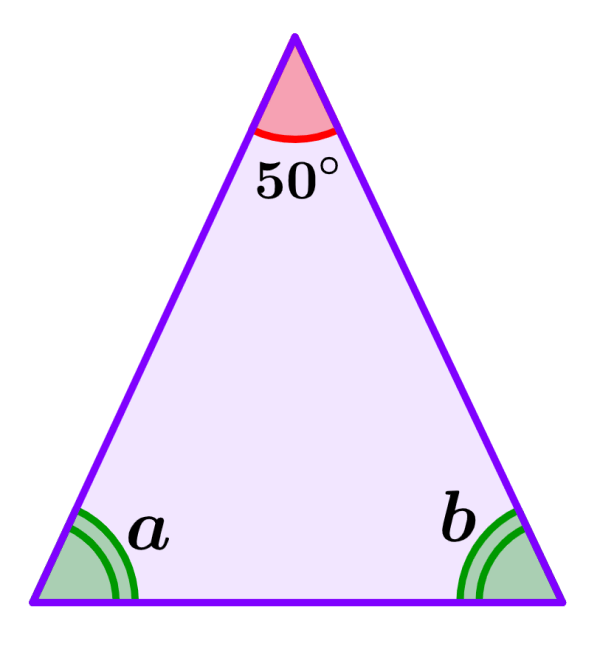
Encuentra las medidas de los ángulos faltantes en el siguiente triángulo isósceles.
Solución: En este caso, tenemos la medida del ángulo que es diferente a los otros dos. Entonces, tenemos que restarlo de 180° para encontrar la suma de los dos ángulos iguales:
180°-50°=130°
130° representa a la suma de los dos ángulos. Dado que estos ángulos son iguales, simplemente dividimos por 2 para encontrar la medida de cada uno:
130°÷2=65°
La medida de los ángulos a y b es 65°.
Véase también
¿Interesado en aprender más sobre suma de ángulos interiores de polígonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
