La suma de ángulos interiores de cualquier polígono siempre permanece constante sin importar si el polígono es regular o irregular. Podemos calcular la suma aplicando una fórmula que usa el número de lados del polígono. A su vez, la fórmula es derivada considerando que todos los polígonos pueden ser divididos en triángulos.
A continuación, conoceremos la fórmula que podemos usar para encontrar la suma de ángulos interiores de polígonos. Luego, usaremos esta fórmula para resolver algunos ejercicios de práctica.
GEOMETRÍA
Relevante para…
Aprender a determinar la suma de ángulos interiores de un polígono.
GEOMETRÍA
Relevante para…
Aprender a determinar la suma de ángulos interiores de un polígono.
Fórmula para encontrar la suma de ángulos interiores de un polígono
La suma de ángulos interiores de cualquier polígono puede ser calculada usando la siguiente fórmula:
| $latex (n-2)\times 180$° |
Aquí, n representa al número de lados del polígono. Por ejemplo, para un pentágono, usamos $latex n=5$ y para un hexágono, usamos $latex n=6$.
Podemos aplicar esta fórmula sin importar si el polígono es regular o irregular ya que un polígono con un determinado número de lados siempre mantiene la misma suma de ángulos interiores.
Por ejemplo, un pentágono tiene 5 lados, por lo que podemos encontrar la suma de sus ángulos al aplicar la fórmula con $latex n=5$:
$latex (n-2)\times 180$°
$latex =(5-2)\times 180$°
$latex =(3)\times 180$°
$latex =540$°
Ahora, para calcular la suma de ángulos interiores de un heptágono, usamos $latex n=7$:
$latex (n-2)\times 180$°
$latex =(7-2)\times 180$°
$latex =(5)\times 180$°
$latex =900$°
En la siguiente tabla, podemos mirar la suma de los ángulos interiores de algunos polígonos comunes:
| Polígono | Número de lados | Suma de ángulos |
| Triángulo | 3 | 180° |
| Cuadrilátero | 4 | 360° |
| Pentágono | 5 | 540° |
| Hexágono | 6 | 720° |
| Heptágono | 7 | 900° |
| Octágono | 8 | 1080° |
| Nonágono | 9 | 1260° |
| Decágono | 10 | 1440° |
Determinar la medida de ángulos interiores individuales de un polígono regular
Un polígono regular tiene todos sus lados con la misma longitud y todos sus ángulos interiores con la misma medida. Esto significa que podemos determinar la medida de uno de los ángulos interiores al dividir la suma total de los ángulos por el número de lados del polígono.
Adicionalmente, podemos obtener una fórmula para la medida individual de un ángulo interior de un polígono regular partiendo de la fórmula para la suma de ángulos. Entonces, tenemos:
| $latex \frac{(n-2)\times 180}{n}$ |
en donde, n representa al número de lados del polígono regular.
Por ejemplo, para determinar la medida de un ángulo interior de un cuadrado, usamos $latex n=4$. Mirando la tabla de arriba, vemos que la suma de ángulos interiores de un cuadrado es igual a 360°. Entonces, al dividir esto por 4, tenemos:
360°÷4=90°
Un ángulo interior de un cuadrado mide 90°.
De igual forma, podemos determinar la medida de los ángulos interiores de un heptágono. Para esto, miramos la tabla de la suma de ángulos y dividimos la suma total por 7. Entonces, vemos que la suma total es 900° y tenemos:
900°÷7=128.57°
Un ángulo interior de un heptágono mide 128.57°.
¿Cómo derivar la fórmula de la suma de ángulos interiores?
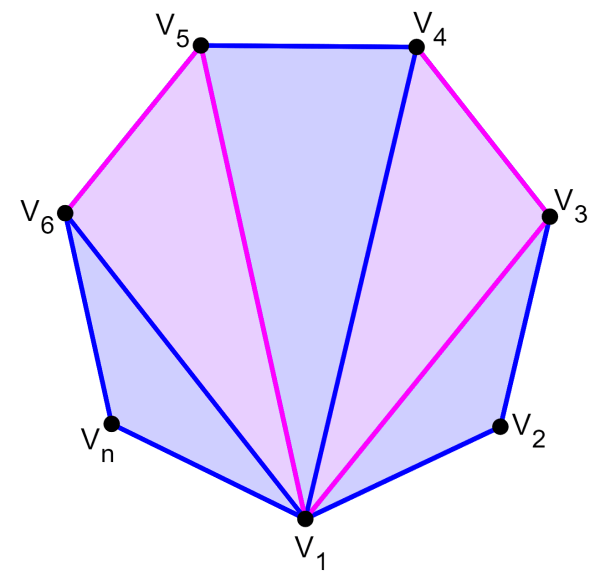
La fórmula de la suma de ángulos interiores de un polígono es derivada considerando que podemos dividir a un polígono en varios triángulos. Por ejemplo, el siguiente polígono que tiene los vértices $latex V_{1}$ hasta $latex V_{n}$.
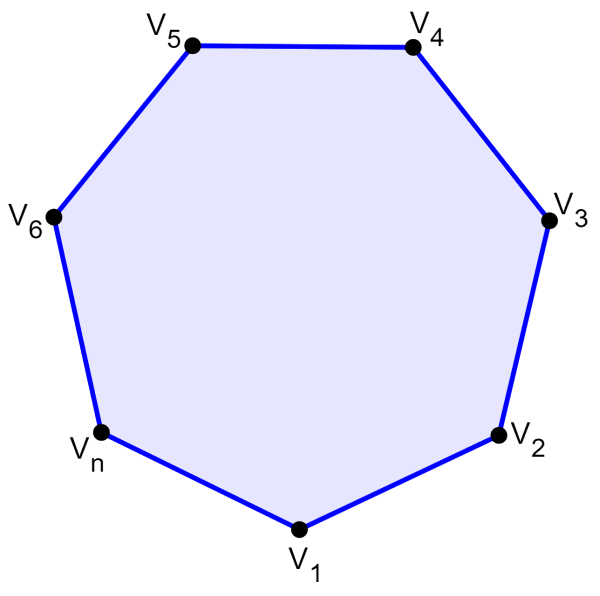
Podemos unir al vértice $latex V_{1}$ con cada vértice a excepción de $latex V_{2}$ y $latex V_{n}$. Entonces, formaremos un número $latex (n-2)$ de triángulos, en donde, n es el número de lados del polígono.
Además, podemos usar el hecho que la suma de ángulos interiores en un triángulo siempre es igual a 180°. Entonces, para un polígono con n lados la suma de todos sus ángulos interiores es igual a $latex (n-2)\times 180$°.
Ejemplos de suma de ángulos interiores de un polígono
EJEMPLO 1
Determina la suma de los ángulos interiores de un polígono irregular de 11 lados.
Solución: La suma de ángulos interiores es la misma sin importar si el polígono es regular o irregular. Entonces, solo tenemos que usar la fórmula con $latex n=11$ y tenemos:
$latex (n-2)\times 180$°
$latex =(11-2)\times 180$°
$latex =(9)\times 180$°
$latex =1620$°
Un polígono irregular de 11 lados tiene una suma de ángulos interiores de 1620°.
EJEMPLO 2
Encuentra la medida de los ángulos individuales de un polígono regular de 9 lados.
Solución: Tenemos que empezar calculando la suma de los ángulos interiores del polígono. Entonces, tenemos:
$latex (n-2)\times 180$°
$latex =(9-2)\times 180$°
$latex =(7)\times 180$°
$latex =1260$°
Ahora, podemos dividir esta suma para 9, ya que el polígono es regular:
1260°÷9=140°
Cada ángulo individual mide 140°
Véase también
¿Interesado en aprender más sobre suma de ángulos interiores de polígonos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
