Las intersecciones de rectas son formadas cuando dos o más rectas comparten uno o más puntos de intersección. Para que las rectas intersequen, las líneas deben tener diferente pendiente y ser no-paralelas. Cuando dos líneas intersecan, dos pares de ángulos verticales opuestos son formados.
A continuación, aprenderemos más detalles sobre las intersecciones de rectas.
GEOMETRÍA
Relevante para…
Aprender sobre las propiedades de las intersecciones de rectas.
GEOMETRÍA
Relevante para…
Aprender sobre las propiedades de las intersecciones de rectas.
¿Qué son las intersecciones de rectas?
Las intersecciones de rectas suceden cuando dos o más líneas se encuentran en un punto común. El punto en el cual las líneas se cruzan es conocido como el punto de intersección.
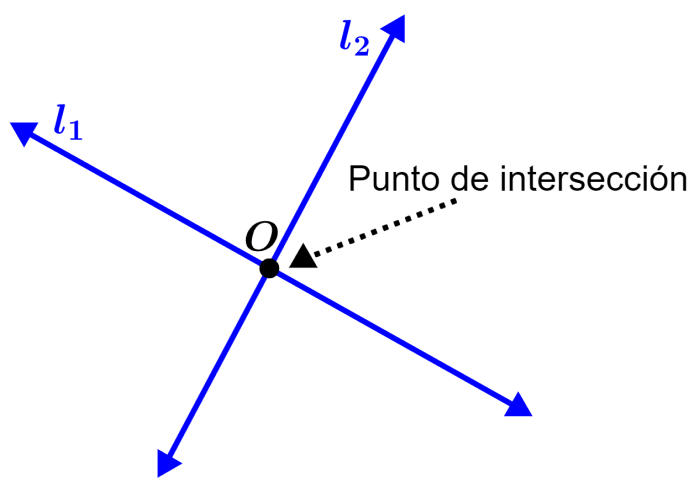
El siguiente diagrama es un ejemplo de intersecciones de rectas. Las líneas $latex l_{1}$ y $latex l_{2}$ se intersecan en el punto O.
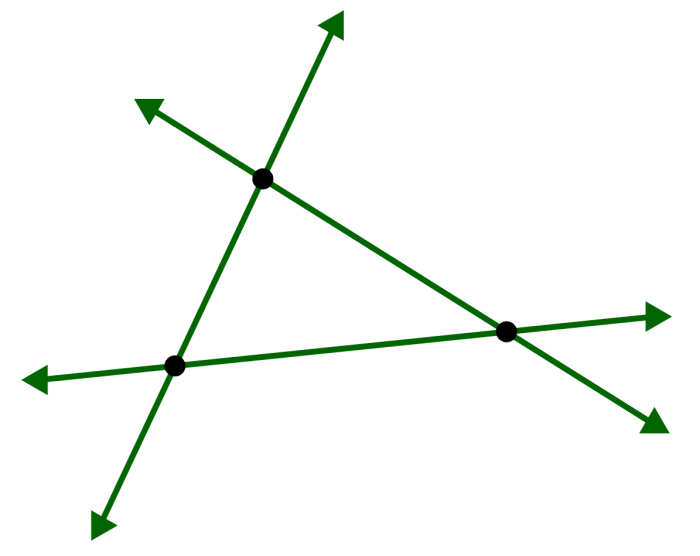
Cuando tenemos tres o más líneas, las rectas pueden compartir más de un punto de intersección como se muestra en el siguiente diagrama.
Propiedades de las intersecciones de rectas
Las siguientes son algunas de las propiedades más importantes de las intersecciones de rectas:
- Dos líneas intersecantes se encuentran en un solo punto llamado el punto de intersección.
- Tres o más líneas intersecantes pueden encontrarse en más de un punto.
- Las líneas intersecantes se encuentran la una con la otra a cualquier ángulo, el cual es mayor que 0° y menor 180°.
- Dos líneas intersecantes forman ángulos verticales opuestos.
¿Qué son las rectas sin intersecciones?
Cuando dos o más rectas no se cruzan la una con la otra, son denominadas rectas sin intersecciones. Todas las líneas intersecarán si es que son extendidas lo suficiente. La única excepción de esto son las líneas paralelas, las cuales no intersecan sin importar cuánto sean extendidas.
Si es queremos dos rectas sin intersecciones, tenemos que asegurarnos de que las rectas sean paralelas, es decir, siempre deben mantener la misma distancia la una de la otra sin importar cuánto las extendamos.
Propiedades de las rectas sin intersecciones
Podemos identificar a las rectas sin intersecciones al considerar que tienen las siguientes propiedades:
- Las rectas sin intersecciones nunca se cruzan la una con la otra y no tienen ningún punto de intersección.
- Estas rectas son equidistantes, es decir, siempre mantienen la misma distancia la una de la otra.
- Las rectas sin intersecciones tienen la misma pendiente.
Ejemplos resueltos de intersecciones de rectas
Los siguientes ejemplos son algunas aplicaciones de las intersecciones de rectas.
EJEMPLO 1
¿Las siguientes líneas son rectas intersecantes o rectas sin intersecciones?
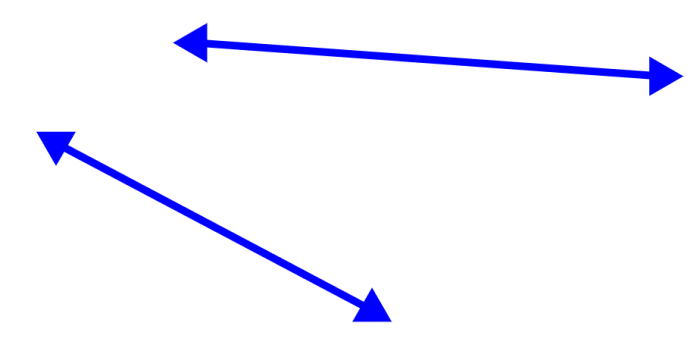
Solución: Las rectas tienen direcciones lo que significa que se extienden indefinidamente hacia ambos lados. Si es que las extendemos lo suficiente, podemos observar que sí se cruzarían, ya que tienen diferentes inclinaciones. Por lo tanto, las rectas son intersecantes.
EJEMPLO 2
¿Cuáles son algunos ejemplos de líneas intersecantes en la vida real?
Solución: Los siguientes son ejemplos de líneas intersecantes:
Cruce de caminos: Cuando dos caminos rectos se encuentran, forman una intersección de rectas.
Tijeras: Las tijeras tienen dos lados, los cuales forman una intersección de rectas.
Rieles de vía férrea: Cuándo hay varias vías férreas, las rieles se cruzan y forman rectas intersecantes.
EJEMPLO 3
¿Cuáles de los siguientes enunciados son verdaderos y cuáles falsos?
- Dos líneas intersecantes forman dos pares de ángulos verticales.
- Tres líneas intersecantes pueden compartir un punto de intersección.
- Dos líneas intersecantes forman cuatro pares de ángulos verticales.
- Tres líneas intersecantes no pueden compartir cuatro puntos comunes de intersección.
Solución: Tenemos lo siguiente:
1. Dos líneas intersecantes forman cuatro ángulos. Cada par de ángulos opuestos el uno del otro son verticales. Entonces, esto es verdadero.
2. Tres líneas intersecantes sí pueden compartir un solo punto de intersección. Entonces, esto es verdadero.
3. Dos líneas intersecantes forman cuatro ángulos, pero solo dos pares de ángulos verticales. Entonces, esto es falso.
4. Tres líneas intersecantes pueden compartir un máximo de tres puntos de intersección. Entonces, esto es verdadero.
Véase también
¿Interesado en aprender más sobre líneas en geometría? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
