Las líneas perpendiculares son dos líneas que intersecan la una con la otra a un ángulo de 90°. También podemos decir que, si es que dos líneas son perpendiculares, su intersección forma un ángulo recto.
A continuación, conoceremos más detalles de las líneas perpendiculares. Aprenderemos sobre sus propiedades y resolveremos algunos ejercicios.
GEOMETRÍA
Relevante para…
Aprender sobre la definición y las propiedades de líneas perpendiculares.
GEOMETRÍA

Relevante para…
Aprender sobre la definición y las propiedades de líneas perpendiculares.
¿Qué son las líneas perpendiculares?
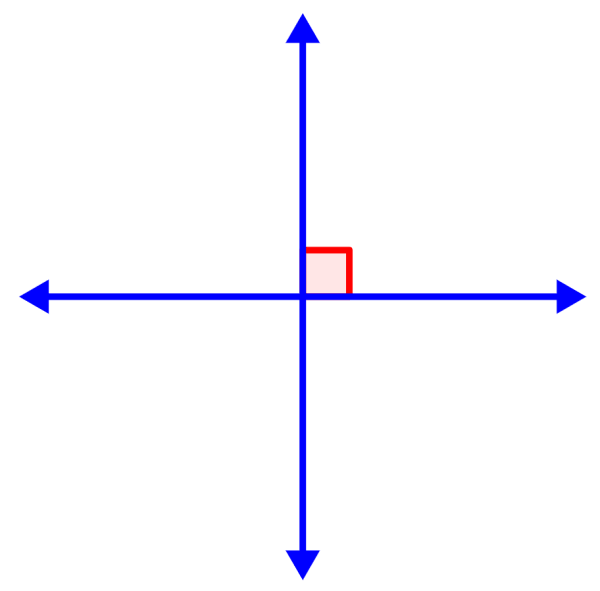
Las líneas perpendiculares son dos líneas rectas que se caracterizan por formar un ángulo de 90° la una con la otra. El ángulo de 90° también es denominado como un ángulo recto y puede ser representado usando un cuadrado pequeño como se muestra en el siguiente diagrama.

Estas líneas intersecan con un ángulo de 90° y por lo tanto, son perpendiculares. Dos líneas tienen que intersecar y formar un ángulo de 90° para ser consideradas perpendiculares.
Propiedades de las líneas perpendiculares
Las líneas perpendiculares pueden ser identificadas porque forman una intersección con forma de «L». El ángulo correspondiente formado en el vértice de intersección es igual a 90°.
Las líneas tienen que intersecar para formar líneas perpendiculares, pero no todas las líneas intersecantes son perpendiculares. Las siguientes son las propiedades de las líneas perpendiculares:
- Las líneas perpendiculares siempre se intersecan la una con la otra.
- El ángulo formado entre dos líneas perpendiculares siempre es de 90°.
- Las pendientes de las líneas perpendiculares son recíprocas y negativas la una de la otra.
- Si es que una línea es perpendicular a una línea que es paralela con otras líneas, entonces, la línea es perpendicular a todas las otras líneas.
¿Cómo determinar si dos líneas son perpendiculares?
Podemos determinar si dos líneas son perpendiculares usando dos métodos principales.
Usar los ángulos
Para que dos líneas sean perpendiculares, su ángulo en el punto de intersección debe ser igual a 90°. El ángulo de 90° es representado con un cuadrado pequeño. Entonces, si es que conocemos el ángulo formado, fácilmente podemos determinar si dos líneas son o no perpendiculares.
Usar las pendientes
Si es que conocemos las ecuaciones de las líneas o podemos derivarlas, podemos usar sus pendientes para determinar si es que las líneas son perpendiculares. Dos líneas son perpendiculares si es que sus pendientes son el recíproco negativo la una de la otra. Es decir, tenemos:
$latex m_{1}=-\frac{1}{m_{2}}$
en donde, $latex m_{1},~m_{2}$ son las pendientes de las líneas.
Diferencias entre las líneas perpendiculares y paralelas
Dos líneas son paralelas cuando no se cruzan la una con la otra sin importar cuánto sean extendidas. Las líneas paralelas siempre permanecen equidistantes.
En el siguiente diagrama, podemos mirar la diferencia entre las líneas paralelas y las líneas perpendiculares. Las líneas AB y CD son perpendiculares, mientras que las líneas EF y GH son paralelas.
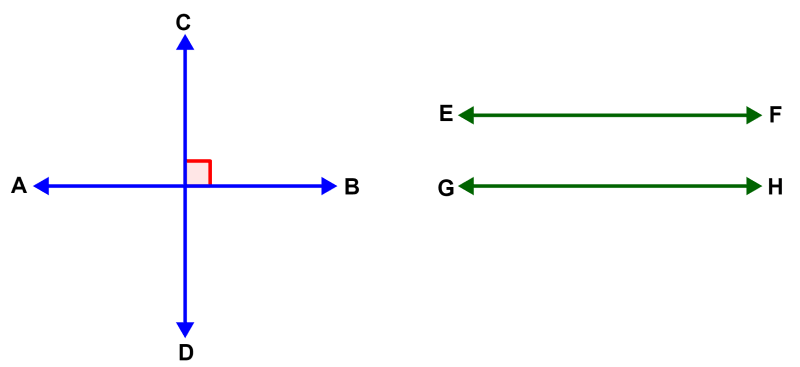
Las líneas paralelas son representadas con el símbolo ||. Por ejemplo, EF||GH indica que las líneas EF y GH son paralelas. Por otra parte, el símbolo usado para representar dos líneas perpendiculares es ⊥. Por ejemplo, AB⊥CD indica que las líneas AB y CD son perpendiculares.
Ejercicios resueltos de líneas perpendiculares
Los siguientes son algunos ejercicios de aplicación de líneas perpendiculares.
EJERCICIO 1
Las siguientes líneas en el diagrama son perpendiculares. ¿Cuáles son las medidas de todos los ángulos formados?

Solución: Los ángulos formados por dos líneas perpendiculares siempre son ángulos rectos. Entonces, todos los ángulos formados son iguales a 90°.
EJERCICIO 2
En el siguiente diagrama, la línea AB es perpendicular a la línea CD. Encuentra el valor del ángulo x.
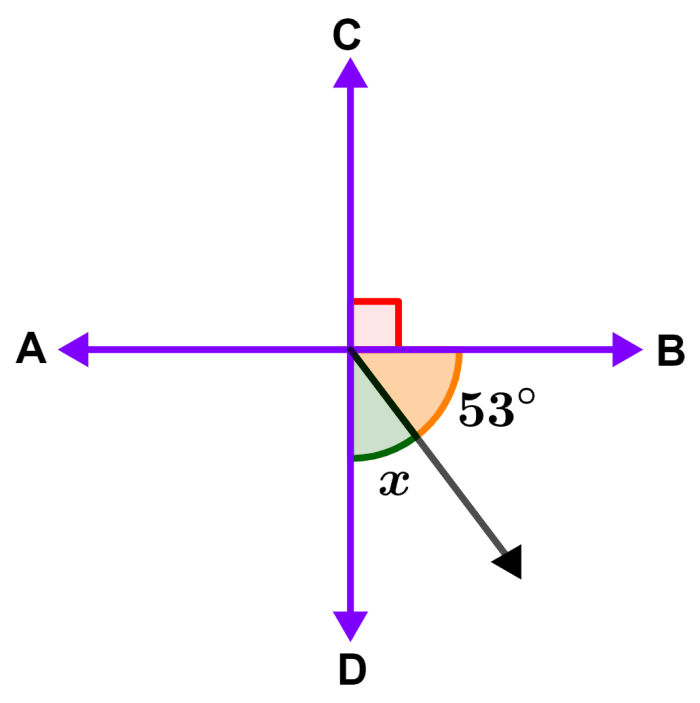
Solución: Las líneas perpendiculares forman ángulos de 90° en el punto de intersección. Esto significa que la suma del ángulo x y de 53° debe ser igual a 90°. Entonces, tenemos:
53°+x=90°
x=90°-53°
x=37°
El ángulo x mide 37°.
Véase también
¿Interesado en aprender más sobre líneas en geometría? Mira estas páginas:


