La distancia entre dos puntos en el plano cartesiano puede ser encontrada al aplicar la fórmula de la distancia y sustituir las coordenadas de los dos puntos dados. A su vez, la fórmula de la distancia es derivada al usar el teorema de Pitágoras en el plano cartesiano, en donde, la distancia representa a la hipotenusa de un triángulo rectángulo.
A continuación, haremos una revisión de la fórmula de la distancia y la usaremos para resolver algunos ejercicios de práctica.
GEOMETRÍA
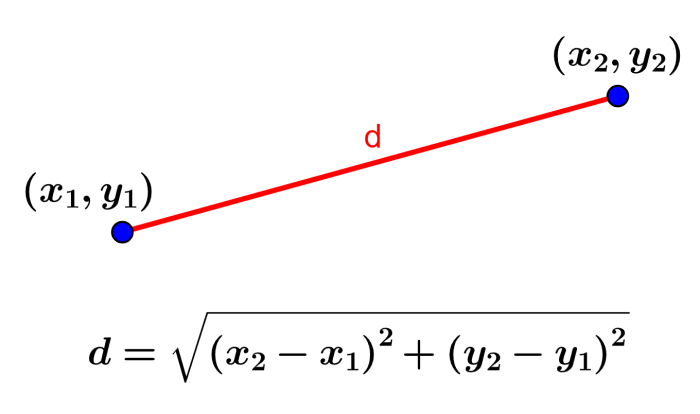
Relevante para…
Aprender a calcular la distancia entre dos puntos con ejercicios.
GEOMETRÍA
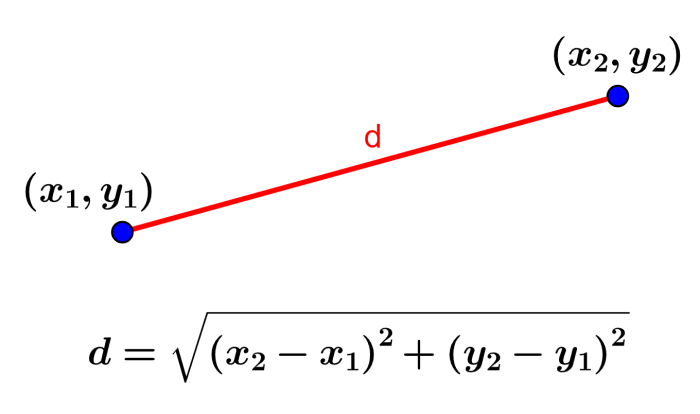
Relevante para…
Aprender a calcular la distancia entre dos puntos con ejercicios.
Revisión de la fórmula para la distancia entre dos puntos
La fórmula para la distancia entre dos puntos es obtenida cuando usamos al teorema de Pitágoras en el plano cartesiano, en donde, la hipotenusa de un triángulo rectángulo representa a la distancia entre los puntos.
Además, al tener los puntos $latex A=(x_{1}, y_{1})$ y $latex B=(x_{2}, y_{2})$, la distancia vertical es igual a $latex |y_{2}-y_{1}|$ y la distancia horizontal es igual a $latex |x_{2}-x_{1}|$. Entonces, cuando aplicamos el teorema de Pitágoras y simplificamos, tenemos:
| Fórmula de la distancia $latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$ |
Adicionalmente, también podemos expandir la fórmula de la distancia al espacio tridimensional de la siguiente manera:
| Fórmula de la distancia en 3D $$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(z_{2}-z_{1})}^2}}$$ |
Distancia entre dos puntos ejercicios resueltos
Las fórmulas de la distancia en 2D y 3D son usadas para resolver los siguientes ejercicios. Intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
Determina la distancia entre los puntos (3, 2) y (6, 6) en el plano cartesiano.
Solución
Escribimos a las coordenadas dadas de la siguiente forma:
- $latex (x_{1}, y_{1})=(3, 2)$
- $latex (x_{2}, y_{2})=(6, 6)$
Aplicando la fórmula de la distancia con las coordenadas dadas, tenemos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(6-3)}^2}+{{(6-2)}^2}}$
$latex =\sqrt{{{(3)}^2}+{{(4)}^2}}$
$latex =\sqrt{9+16}$
$latex =\sqrt{25}$
$latex =5$
La distancia entre los dos puntos es 5.
EJERCICIO 2
¿Cuál es la distancia entre los puntos (-1, -3) y (5, 7)?
Solución
Tenemos los siguientes valores:
- $latex (x_{1}, y_{1})=(-1, -3)$
- $latex (x_{2}, y_{2})=(5, 7)$
En este caso, tenemos coordenadas negativas. Sin embargo, la fórmula de la distancia aplica sin importar los signos de las coordenadas:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(5-(-1))}^2}+{{(7-(-3))}^2}}$
$latex =\sqrt{{{(6)}^2}+{{(10)}^2}}$
$latex =\sqrt{36+100}$
$latex =\sqrt{136}$
$latex =11.66$
La distancia entre los puntos es igual a 11.66.
EJERCICIO 3
Si es que tenemos los puntos (-4, -6) y (-1, 5), ¿cuál es su distancia?
Solución
Podemos escribir de la siguiente forma:
- $latex (x_{1}, y_{1})=(-4, -6)$
- $latex (x_{2}, y_{2})=(-1, 5)$
Al aplicar la fórmula de la distancia, tenemos:
$latex d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}}$
$latex =\sqrt{{{(-1-(-4))}^2}+{{(5-(-6))}^2}}$
$latex =\sqrt{{{(3)}^2}+{{(11)}^2}}$
$latex =\sqrt{9+121}$
$latex =\sqrt{130}$
$latex =11.4$
La distancia entre los puntos es igual a 11.4.
EJERCICIO 4
Tenemos a los puntos (1, 2, 3) y (3, 4, 5) ubicados en el espacio tridimensional. ¿Cuál es su distancia?
Solución
Escribimos a las coordenadas de la siguiente manera:
- $latex (x_{1}, y_{1}, z_{1})=(1, 2, 3)$
- $latex (x_{2}, y_{2}, z_{2})=(3, 4, 5)$
En este caso, los puntos dados están en el espacio tridimensional. Podemos encontrar su distancia al usar la fórmula de la distancia en 3D:
$$d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(y_{2}-y_{1})}^2}}$$
$$=\sqrt{{{(3-1)}^2}+{{(4-2)}^2}+{{(5-3)}^2}}$$
$latex =\sqrt{{{(2)}^2}+{{(2)}^2}+{{(2)}^2}}$
$latex =\sqrt{4+4+4}$
$latex =\sqrt{12}$
$latex =3.47$
La distancia es igual a 3.47.
EJERCICIO 5
Si es que tenemos a los puntos (-3, 4, -2) y (2, 6, 3), ¿cuál es su distancia?
Solución
Podemos escribir de la siguiente manera:
- $latex (x_{1}, y_{1}, z_{1})=(-3, 4, -2)$
- $latex (x_{2}, y_{2}, z_{2})=(2, 6, 3)$
Similar al ejercicio anterior, tenemos que usar la fórmula de la distancia en 3D con las coordenadas dadas. Entonces, tenemos:
$$ d=\sqrt{{{(x_{2}-x_{1})}^2}+{{(y_{2}-y_{1})}^2}+{{(y_{2}-y_{1})}^2}}$$
$$=\sqrt{{{(2-(-3))}^2}+{{(6-4)}^2}+{{(3-(-2))}^2}}$$
$latex =\sqrt{{{(5)}^2}+{{(2)}^2}+{{(5)}^2}}$
$latex =\sqrt{25+2+25}$
$latex =\sqrt{52}$
$latex =7.21$
La distancia es igual a 7.21.
Distancia entre dos puntos ejercicios para resolver
Usa las fórmulas de la distancia tanto en 2D como en 3D para resolver los siguientes ejercicios. En caso de necesitar ayuda con esto, puedes mirar los ejercicios resueltos de arriba.
Véase también
¿Interesado en aprender más sobre punto medio y distancia en el plano? Mira estas páginas:


