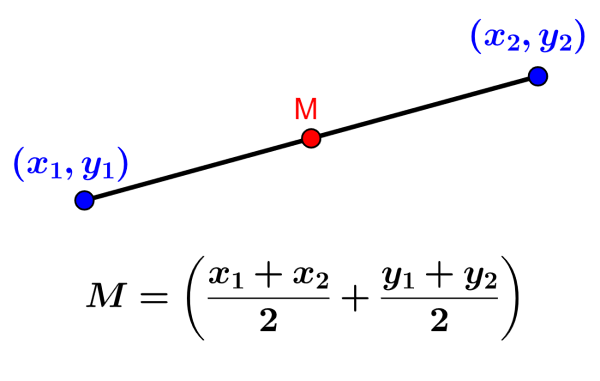
El punto medio de un segmento representa al punto que se ubica exactamente en la mitad de los dos puntos extremos del segmento. El punto medio puede ser encontrado al dividir a la suma de las coordenadas x por 2 y dividir a la suma de las coordenadas y por 2.
A continuación, conoceremos la fórmula que podemos usar para calcular el punto medio de un segmento. Además, usaremos esa fórmula para resolver algunos ejercicios de práctica.
¿Qué es el punto medio?
El punto medio es un punto que se ubica exactamente en la mitad de un segmento de línea que une a dos puntos. Por ejemplo, si es que tenemos dos puntos y los unimos con un segmento de línea, el punto medio se ubicará en la mitad de ese segmento y será equidistante a ambos puntos.
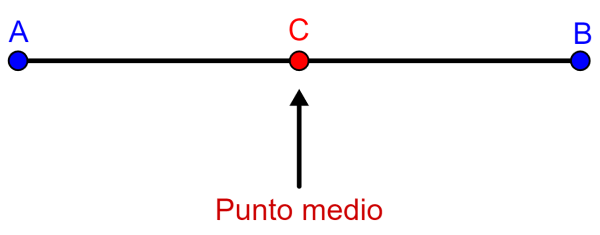
En el siguiente diagrama tenemos los puntos A y B, los cuales están unidos por un segmento. El punto C es el punto medio, ya que está exactamente en la mitad del segmento. Para calcular la ubicación del punto medio, simplemente tenemos que medir la longitud del segmento y dividir por 2.
Un punto medio puede ser calculado solo cuando tenemos a un segmento que une a dos puntos, ya que tiene una ubicación definida. El punto medio no puede ser calculado para una línea o un rayo, ya que una línea tiene dos extremos que se extienden indefinidamente y un rayo tiene un extremo que se extiende indefinidamente.
Fórmula para el punto medio de un segmento
La fórmula para el punto medio de un segmento es derivada usando las coordenadas de los puntos extremos del segmento. El punto medio es igual a la mitad de la suma de las coordenadas en x de los puntos y a la mitad de las coordenadas en y de los puntos.
Entonces, si es que tenemos los puntos A y B con las coordenadas $latex A=(x_{1}, y_{1})$ y $latex B=(x_{2}, y_{2})$, la fórmula del punto medio es:
Fórmula del punto medio
$$M=\left( \frac{x_{1}+x_{2}}{2}+\frac{y_{1}+y_{2}}{2}\right)$$
El punto medio será expresado como las coordenadas $latex M=(x_{3}, y_{3})$.
10 Ejercicios de punto medio de un segmento resueltos
EJERCICIO 1
Encuentra el punto medio de un segmento que une a los puntos (2, 5) y (6, 9).
Solución
Tenemos a las siguientes coordenadas
- $latex (x_{1}, y_{1})=(2, 5)$
- $latex (x_{2}, y_{2})=(6, 9)$
Ahora, usamos la fórmula del punto medio con las coordenadas dadas
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{2+6}{2},\frac{5+9}{2}\right)$$
$$=\left(\frac{8}{2},\frac{14}{2}\right)$$
$latex =(4,7)$
El punto medio es $latex M=(4, 7)$.
EJERCICIO 2
¿Cuál es el punto medio entre los puntos (2, 6) y (8, 12)?
Solución
Tenemos las siguientes coordenadas:
- $latex (x_{1}, y_{1})=(2, 6)$
- $latex (x_{2}, y_{2})=(8, 12)$
Usamos las coordenadas dadas en la fórmula del punto medio:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{2+8}{2},\frac{6+12}{2}\right)$$
$$=\left(\frac{10}{2},\frac{18}{2}\right)$$
$latex =(5, 9)$
Las coordenadas del punto medio son $latex M=(5, 9)$.
EJERCICIO 3
¿Cuál es el punto medio de un segmento que une a los puntos (4, 7) y (9, 10)?
Solución
Podemos escribir de la siguiente forma:
- $latex (x_{1}, y_{1})=(4, 7)$
- $latex (x_{2}, y_{2})=(9, 10)$
Aplicando la fórmula del punto medio con las coordenadas dadas, tenemos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{4+9}{2},\frac{7+10}{2}\right)$$
$$=\left(\frac{13}{2},\frac{17}{2}\right)$$
El punto medio es $latex M=\left(\frac{13}{2},\frac{17}{2}\right)$.
EJERCICIO 4
Determina el punto medio entre los puntos (5, 7) y (9, 13).
Solución
Tenemos los siguientes puntos:
- $latex (x_{1}, y_{1})=(5, 7)$
- $latex (x_{2}, y_{2})=(9, 13)$
Aplicamos la fórmula del punto medio con estos puntos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{5+9}{2},\frac{7+13}{2}\right)$$
$$=\left(\frac{14}{2},\frac{20}{2}\right)$$
$latex =(7,10)$
Las coordenadas del punto medio son $latex M=(7, 10)$.
EJERCICIO 5
Si es que tenemos los puntos (-4, -2) y (6, 5) unidos por un segmento, ¿cuál es su punto medio?
Solución
Tenemos los siguientes valores:
- $latex (x_{1}, y_{1})=(-4, -2)$
- $latex (x_{2}, y_{2})=(6, 5)$
En este caso, tenemos coordenadas negativas, sin embargo, simplemente aplicamos la fórmula del punto medio como en los ejercicios anteriores:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-4+6}{2},\frac{-2+5}{2}\right)$$
$$=\left(\frac{2}{2},\frac{3}{2}\right)$$
$$=\left(1,\frac{3}{2}\right)$$
El punto medio tiene las coordenadas $latex M=\left(1,\frac{3}{2}\right)$.
EJERCICIO 6
Encuentra el punto medio si es que tenemos los puntos (-5, -6) y (6, -2).
Solución
Escribimos a las coordenadas de la siguiente manera:
- $latex (x_{1}, y_{1})=(-5, -6)$
- $latex (x_{2}, y_{2})=(6, -2)$
En este caso, tenemos coordenadas negativas, pero simplemente usamos la fórmula del punto medio como en los anteriores ejercicios:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-5+6}{2},\frac{-6-2}{2}\right)$$
$$=\left(\frac{1}{2},\frac{-8}{2}\right)$$
$$=\left(\frac{1}{2}, -4\right)$$
El punto medio tiene las coordenadas $latex M=\left(\frac{1}{2}, -4\right)$.
EJERCICIO 7
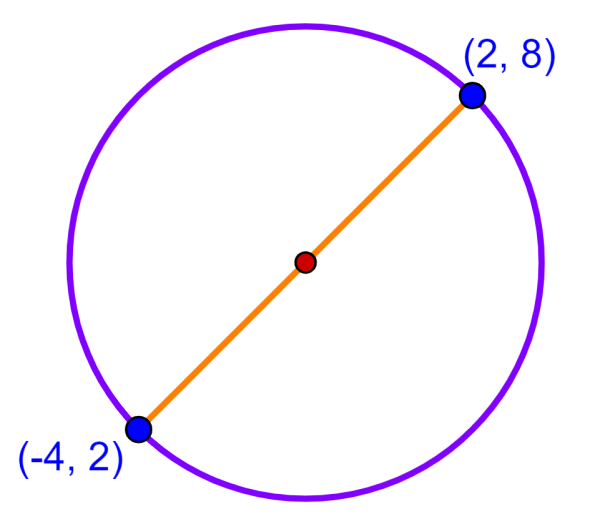
El diámetro de un círculo tiene los puntos extremos (-4, 2) y (2, 8). ¿Cuáles son las coordenadas del centro del círculo?
Solución
El centro del círculo divide al diámetro en dos partes iguales. Eso significa que, para encontrar el centro, tenemos que encontrar las coordenadas del punto medio del diámetro. Entonces, empezamos con las coordenadas:
- $latex (x_{1}, y_{1})=(-4,2)$
- $latex (x_{2}, y_{2})=(2,8)$
Ahora, aplicamos la fórmula del punto medio con estas coordenadas:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-4+2}{2},\frac{2+8}{2}\right)$$
$$=\left(\frac{-2}{2},\frac{10}{2}\right)$$
$latex =(-1,5)$
Las coordenadas del centro del círculo son $latex (-1, 5)$.
EJERCICIO 8
Los puntos extremos de un segmento son (p, 4) y (8, 10). Encuentra el valor de p si es que el punto medio es (3, 7).
Solución
Escribimos las coordenadas dadas:
- $latex (x_{1}, y_{1})=(p, 4)$
- $latex (x_{2}, y_{2})=(8, 10)$
Ahora, podemos aplicar la fórmula del punto medio con los valores conocidos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{p+8}{2},\frac{4+10}{2}\right)$$
En este caso, tenemos que encontrar el valor de p que es parte de las coordenadas x del punto medio. Entonces, solo consideramos al componente x, formamos una ecuación y resolvemos para p. Sabemos que la coordenada en x del punto medio es 3, por lo que tenemos
$$3=\left(\frac{p+8}{2}\right)$$
$latex 6=p+8$
$latex p=-2$
El valor de p es -2.
EJERCICIO 9
Si es que el punto medio de un segmento es (-2, 1) y sus puntos extremos son (-6, q) y (2, 4), ¿cuál es el valor de q?
Solución
Tenemos las siguientes coordenadas:
- $latex (x_{1}, y_{1})=(-6, x)$
- $latex (x_{2}, y_{2})=(2, -4)$
Cuando aplicamos la fórmula del punto medio, tenemos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{-6+2}{2},\frac{q+4}{2}\right)$$
Para encontrar el valor de q, formamos una ecuación con la coordenada y del punto medio:
$$\left(\frac{q+4}{2}\right)=1$$
$latex q+4=2$
$latex q=-2$
El valor de q es -2.
EJERCICIO 10
El punto medio de un segmento tiene las coordenadas (-3, -4). Si es que los puntos extremos del segmento son (3, -1) y (m, -7), encuentra el valor de m.
Solución
Empezamos con las siguientes coordenadas:
- $latex (x_{1}, y_{1})=(3, -1)$
- $latex (x_{2}, y_{2})=(m, -7)$
Aplicando la fórmula del punto medio, tenemos:
$$M=\left(\frac{x_{1}+x{2}}{2},\frac{y_{1}+y{2}}{2}\right)$$
$$=\left(\frac{3+m}{2},\frac{-1-7}{2}\right)$$
Similar a los ejercicios anteriores, solo tenemos que considerar a las coordenadas x del punto medio y formar una ecuación:
$$\left(\frac{3+m}{2}\right)=-3$$
$latex 3+m=-6$
$latex m=-9$
El valor de m es -9.
Punto medio de un segmento ejercicios para resolver


Un segmento está definido por los puntos (p, 3) y (5, 13). Si es que el punto medio es (1, 8), ¿cuál es el valor de p?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre punto medio y distancia en el plano? Mira estas páginas: