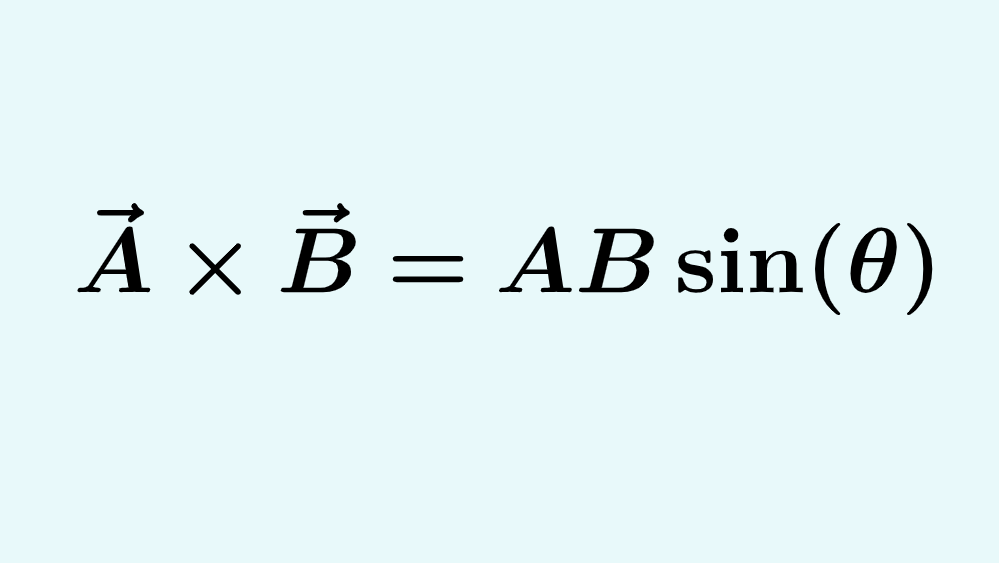El producto vectorial, o producto cruz de dos vectores, puede ser calculado usando dos métodos principales. Podemos usar las magnitudes de los vectores y el ángulo entre sus direcciones. Alternativamente, podemos usar los componentes de ambos vectores.
En este artículo, resolveremos varios ejercicios en los que aplicaremos estos dos métodos. Luego, veremos algunos ejercicios para resolver.
10 Ejercicios resueltos de producto vectorial de vectores
EJERCICIO 1
Tenemos un vector $latex \vec{A}$ con una magnitud de 8 unidades en la dirección el eje $latex x$. El vector $latex \vec{B}$ tiene una magnitud de 6 unidades y está en el plano $latex xy$ formando un ángulo de 30° con el eje $latex +x$.
Encuentra el producto vectorial $latex \vec{C}=\vec{A}\times \vec{B}$.
Solución
Tenemos la siguiente información:
- Magnitud de $latex \vec{A}$: $latex ~A=8$
- Magnitud de $latex \vec{B}$: $latex ~B=6$
- Ángulo entre vectores: $latex ~\theta=30^{\circ}$
Entonces, podemos usar la siguiente fórmula para encontrar la magnitud del vector $latex \vec{C}$:
$latex C=AB\sin(\theta)$
$latex =(8)(6)\sin(30^{\circ})$
$latex =24$
Para encontrar la dirección del vector $latex \vec{C}$, usamos el siguiente diagrama y la regla de la mano derecha:
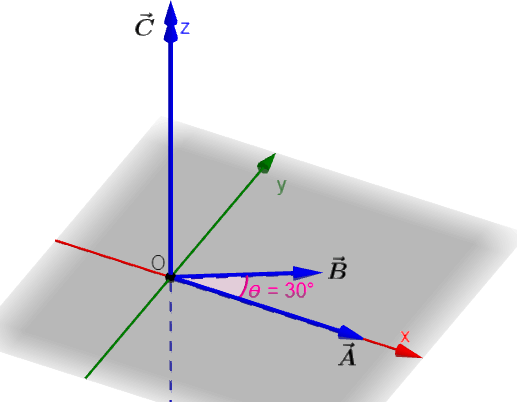
Por la regla de la mano derecha, la dirección de $latex \vec{A}\times \vec{B}$ es a lo largo de $latex +z$ o en la dirección $latex \hat{k}$. Entonces,
$latex \vec{C}=\vec{A}\times \vec{B}=24\hat{k}$
EJERCICIO 2
Encuentra el producto vectorial $latex \vec{A} \times \vec{B}$ de los siguientes vectores:
$latex \vec{A} = 2 \hat{i} -3 \hat{j} +4 \hat{k}$
$latex \vec{B} = 1 \hat{i} +5 \hat{j} -2 \hat{k}$
Solución
En este caso, conocemos los componentes de ambos vectores. Entonces, podemos encontrar los componentes del producto vectorial usando la siguiente fórmula:
$latex C_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex C_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex C_{z} =A_{x} B_{y} – A_{y} B_{x}$
en donde $latex \vec{C}=\vec{A} \times \vec{B}$. Entonces:
$latex \vec{A} \times \vec{B} = ((-3)(-2) – (4)(5))\hat{i} +( (4)(1)-(2)(-2))\hat{j} + ((2) (5) – (-3) (1))\hat{k}$
$latex \vec{A} \times \vec{B}=-14\hat{i} + 8\hat{j} + 13\hat{k}$
EJERCICIO 3
Encuentra el producto vectorial $latex \vec{C}=\vec{A}\times \vec{B}$ de los siguientes vectores:
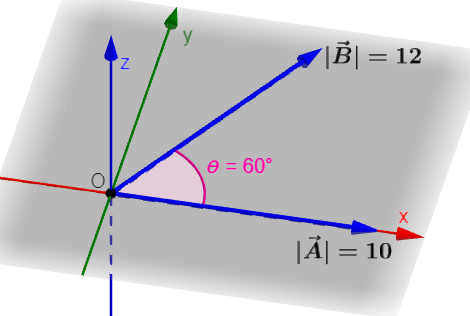
Solución
Podemos observar lo siguiente:
- Magnitud de $latex \vec{A}$: $latex ~A=10$
- Magnitud de $latex \vec{B}$: $latex ~B=12$
- Ángulo entre vectores: $latex ~\theta=60^{\circ}$
Similar al ejercicio 1, podemos usar la siguiente fórmula para encontrar la magnitud del vector $latex \vec{C}$:
$latex C=AB\sin(\theta)$
$latex =(10)(12)\sin(60^{\circ})$
$latex =103.92$
Usando el diagrama dado y la regla de la mano derecha, podemos determinar que la dirección de $latex \vec{A}\times \vec{B}$ es $latex \hat{k}$. Entonces,
$latex \vec{C}=\vec{A}\times \vec{B}=103.92\hat{k}$
EJERCICIO 4
Encuentra el producto vectorial $latex \vec{C} \times \vec{D}$ con los siguientes vectores:
$latex \vec{C} = 3 \hat{i} +0 \hat{j} -7 \hat{k}$
$latex \vec{D} =-4 \hat{i}+ 6 \hat{j} 2 \hat{k}$
Solución
Vamos a usar las siguientes fórmulas para encontrar los componentes del producto vectorial:
$latex R_{x}=C_{y} D_{z} – C_{z} D_{y}$
$latex R_{y}=C_{z} D_{x}-C_{x} D_{z}$
$latex R_{z} =C_{x} D_{y} – C_{y} D_{x}$
Entonces, tenemos:
$latex \vec{C} \times \vec{D} = ((0)(2) – (-7)(6)) \hat{i} +((-7)(-4)-(3)(2) )\hat{j} + ((3)(6) – (0)(-4))\hat{k}$
$latex \vec{A} \times \vec{B}=42 \hat{i} +22 \hat{j} +18\hat{k}$
EJERCICIO 5
Encuentra el producto vectorial $latex \vec{A}\times \vec{B}$:
$latex \vec{A} = 5 \hat{i} -2 \hat{j}+ 3\hat{k}$
$latex \vec{B} =1 \hat{i} +4 \hat{j} -1\hat{k}$
Solución
Usamos las siguientes fórmulas para encontrar los componentes del producto vectorial:
$latex R_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex R_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex R_{z} =A_{x} B_{y} – A_{y} B_{x}$
Entonces, tenemos:
$latex \vec{A} \times \vec{B} = ((-2)(-1) – (3)(4)) \hat{i} +((3)(1)-(5)(-1))\hat{j} + ((5)(4) – (-2)(1))\hat{k}$
$latex \vec{A} \times \vec{B}=-10 \hat{i} +8 \hat{j} +22\hat{k}$
EJERCICIO 6
Encuentra el producto vectorial de los dos vectores siguientes usando sus magnitudes y el ángulo entre ellos:
- Magnitud de vector K: $latex ~|\vec{K}| = 3$
- Magnitud de vector L: $latex ~|\vec{L}| = 4$
- Ángulo entre $latex \vec{K}~$ y $latex ~\vec{L}$: $latex ~\theta= 60^\circ$
Solución
Usando la información dada, podemos aplicar la fórmula del producto vectorial para encontrar la magnitud de $latex \vec{R}$:
$latex R=KL\sin(\theta)$
$latex =(3)(4)\sin(60^{\circ})$
$latex =12\left(\dfrac{\sqrt{3}}{2}\right)$
$latex = 6\sqrt{3}$
Ten en cuenta que esto es solo la magnitud; para encontrar la dirección del producto vectorial, necesitaríamos las direcciones de los dos vectores dados.
EJERCICIO 7
Encuentra el producto vectorial $latex \vec{M}\times \vec{N}$ de los dos vectores siguientes:
- Magnitud del vector $latex \vec{M}$: $latex ~|\vec{M}| = 5$
- Magnitud del vector $latex \vec{N}$: $latex ~|\vec{N}| = 7$
- Ángulo entre $latex \vec{M}~$ y $latex ~\vec{M}$: $latex ~\theta= 45^\circ$
Solución
Con la información dada, aplicamos la fórmula de la magnitud del producto vectorial de la siguiente forma:
$latex R=MN\sin(\theta)$
$latex =(5)(7)\sin(45^{\circ})$
$latex= 35\left(\dfrac{\sqrt{2}}{2}\right)$
$latex = \dfrac{35\sqrt{2}}{2}$
Similar al ejercicio anterior, necesitamos más información sobre los vectores para determinar la dirección del producto vectorial.
EJERCICIO 8
¿Cuál es la magnitud del vector $latex \vec{R}$ si es que $latex \vec{R}=\vec{A}\times \vec{B}$?
- Magnitud del vector $latex \vec{A}$: $latex ~|\vec{A}| = 8$
- Magnitud del vector $latex \vec{B}$: $latex ~|\vec{B}| = 6$
- Ángulo entre $latex \vec{A}~$ y $latex ~\vec{B}$: $latex ~\theta= 120^\circ$
Solución
Usamos los datos dados en la fórmula de la magnitud del producto vectorial:
$latex R=AB\sin(\theta)$
$latex =(8)(6)\sin(120^{\circ})$
$latex= 48\left(\dfrac{\sqrt{3}}{2}\right)$
$latex = 24\sqrt{3}$
Para determinar la dirección del producto vectorial, necesitamos las direcciones de los vectores dados.
EJERCICIO 9
Encuentra el producto vectorial $latex \vec{A}\times \vec{B}$ usando los siguientes vectores:
$latex \vec{A} = 6 \hat{i} -3 \hat{j} +1 \hat{k}$
$latex \vec{B} = 2 \hat{i} +4 \hat{j} -5 \hat{k}$
Solución
Dado que conocemos los componentes de los vectores, podemos usar las siguientes fórmulas para encontrar los componentes del vector resultante del producto vectorial:
$latex R_{x}=A_{y} B_{z} – A_{z} B_{y}$
$latex R_{y}=A_{z} B_{x}-A_{x} B_{z}$
$latex R_{z} =A_{x} B_{y} – A_{y} B_{x}$
Al usar los valores dados, tenemos:
$latex \vec{A} \times \vec{B} = ((-3)(-5) – (1)(4)) \hat{i} +((1)(2)-(6)(-5))\hat{j} + ((6)(4) – (-3)(2))\hat{k}$
$latex \vec{A} \times \vec{B}=11 \hat{i} +32\hat{j} +30\hat{k}$
EJERCICIO 10
Tenemos los vectores $latex \vec{M}=2\hat{i} − 3\hat{j} + \hat{k}~$ y $latex ~\vec{B}= \hat{i} + 2\hat{j} − 3\hat{k}$. Demuestra que $latex \vec{A}\times \vec{B}$ es perpendicular a $latex \vec{A}$ y a $latex \vec{B}$.
Solución
Empecemos encontrando el producto vectorial $latex \vec{A}\times \vec{B}$:
$latex \vec{A}\times \vec{B}=((−3)(−3) − (2)(1))\hat{i} + ((1)(1) − (−3)(2))\hat{j} ++((2)(2) − (1)(−3))\hat{k}$
$latex =7\hat{i} +7\hat{j} + 7\hat{k}$
Para demostrar que $latex \vec{A}\times \vec{B}$ es perpendicular a $latex \vec{A}$, debemos tener $latex (\vec{A}\times \vec{B})\cdot \vec{A}=0$:
$$(\vec{A}\times \vec{B})\cdot \vec{A}=\begin{pmatrix} 7 \\ 7 \\ 7 \end{pmatrix}\cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$$
$latex = 14 − 21 + 7 = 0$
Para demostrar que $latex \vec{A}\times \vec{B}$ es perpendicular a $latex \vec{B}$, debemos tener $latex (\vec{A}\times \vec{B})\cdot \vec{B}=0$:
$$(\vec{A}\times \vec{B})\cdot \vec{B}=\begin{pmatrix} 7 \\ 7 \\ 7 \end{pmatrix}\cdot \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix}$$
$latex = 7+14-21 = 0$
Producto vectorial de vectores – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
