Existen dos fórmulas principales que pueden ser aplicadas para calcular el producto vectorial de dos vectores. La primera fórmula usa las magnitudes de los vectores y el ángulo entre sus direcciones. La segunda fórmula usa los componentes de los vectores.
A continuación, conoceremos las dos fórmulas para calcular el producto vectorial de dos vectores. Luego, veremos algunas de las propiedades más importantes del producto vectorial.
FÍSICA
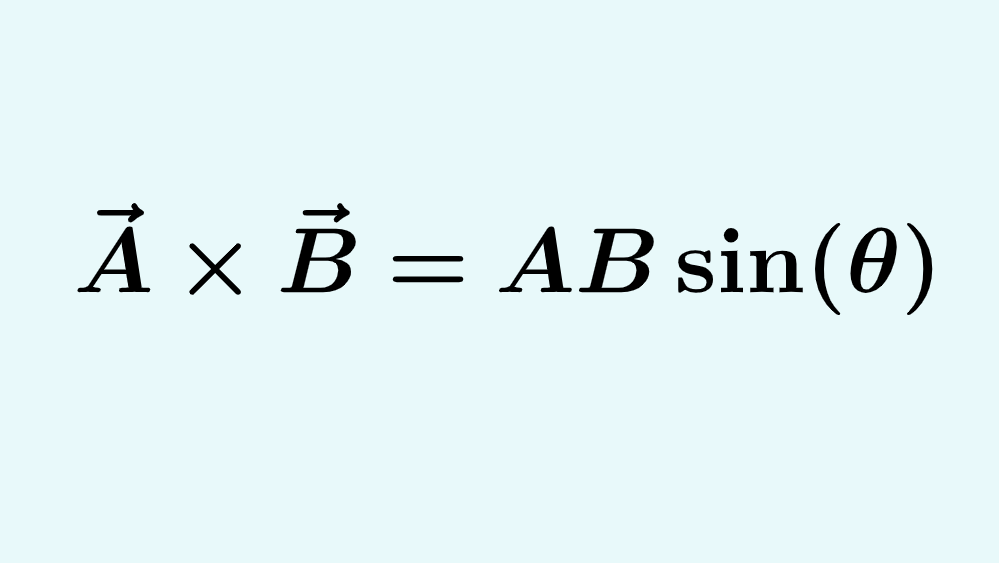
Relevante para…
Aprender sobre las fórmulas y propiedades del producto vectorial de vectores.
FÍSICA
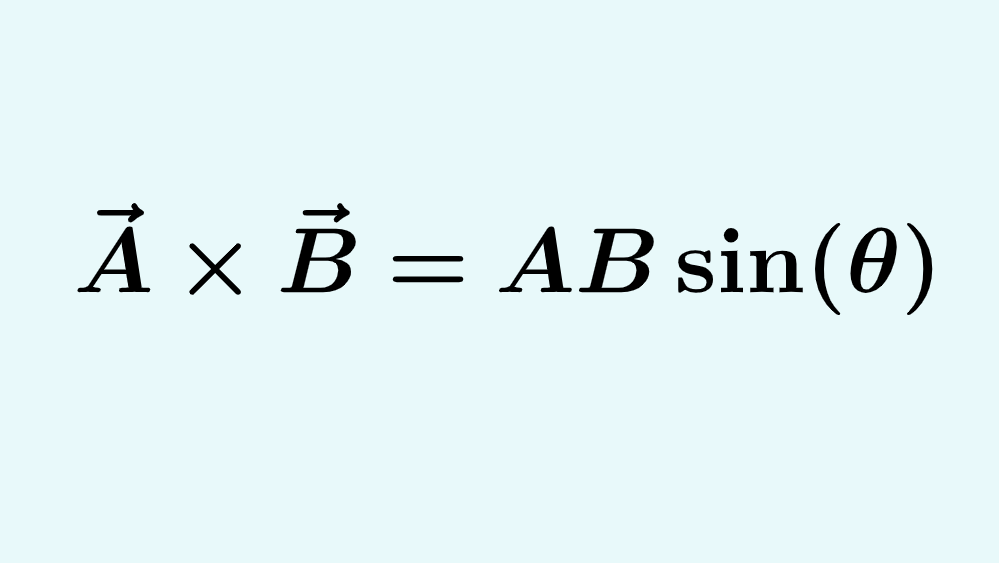
Relevante para…
Aprender sobre las fórmulas y propiedades del producto vectorial de vectores.
Producto vectorial usando magnitudes y ángulo entre vectores
El producto vectorial de dos vectores $latex \vec{A}$ y $latex \vec{B}$ es denotado por $latex \vec{A} \times \vec{B}$. El resultado del producto vectorial es un vector.
Cuando tenemos las magnitudes de los vectores y el ángulo entre sus direcciones, la magnitud de su producto vectorial es calculado con la siguiente fórmula:
$$\vec{A}\times \vec{B}=AB\sin(\theta)$$
en donde, $latex A$ y $latex B$ son las magnitudes de $latex \vec{A}$ y $latex \vec{B}$ respectivamente, y $latex \theta$ es el ángulo entre los vectores.
Vamos a usar el siguiente diagrama para dar una interpretación geométrica del producto vectorial:
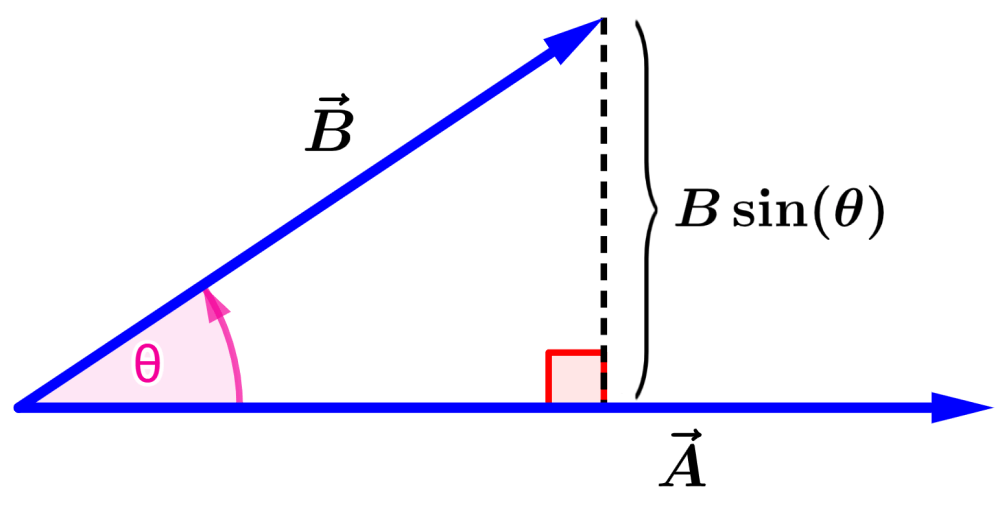
Vemos que $latex B \sin(\theta)$ es el componente de $latex \vec{B}$ que es perpendicular a la dirección de $latex \vec{A}$.
Alternativamente, la magnitud de $latex \vec{A}\times \vec{B}$ es la magnitud de $latex \vec{B}$ multiplicado por el componente de $latex \vec{A}$ perpendicular a la dirección de $latex \vec{B}$.
Dirección del producto vectorial
El resultado del producto vectorial es un vector, por lo que tiene una magnitud y una dirección.
La dirección del producto vectorial es perpendicular al plano que contiene a los vectores $latex \vec{A}$ y $latex \vec{B}$. Es decir, la dirección del producto vectorial es perpendicular a ambos vectores.
Sin embargo, siempre hay dos direcciones perpendiculares a un plano dado, una a cada lado del plano. Podemos escoger la dirección correcta de la siguiente forma:
Usamos nuestra mano derecha para rotar desde el vector $latex \vec{A}$ hasta la dirección del vector $latex \vec{B}$. Nuestros dedos deben apuntar en la dirección de la rotación, como se muestra en la figura:
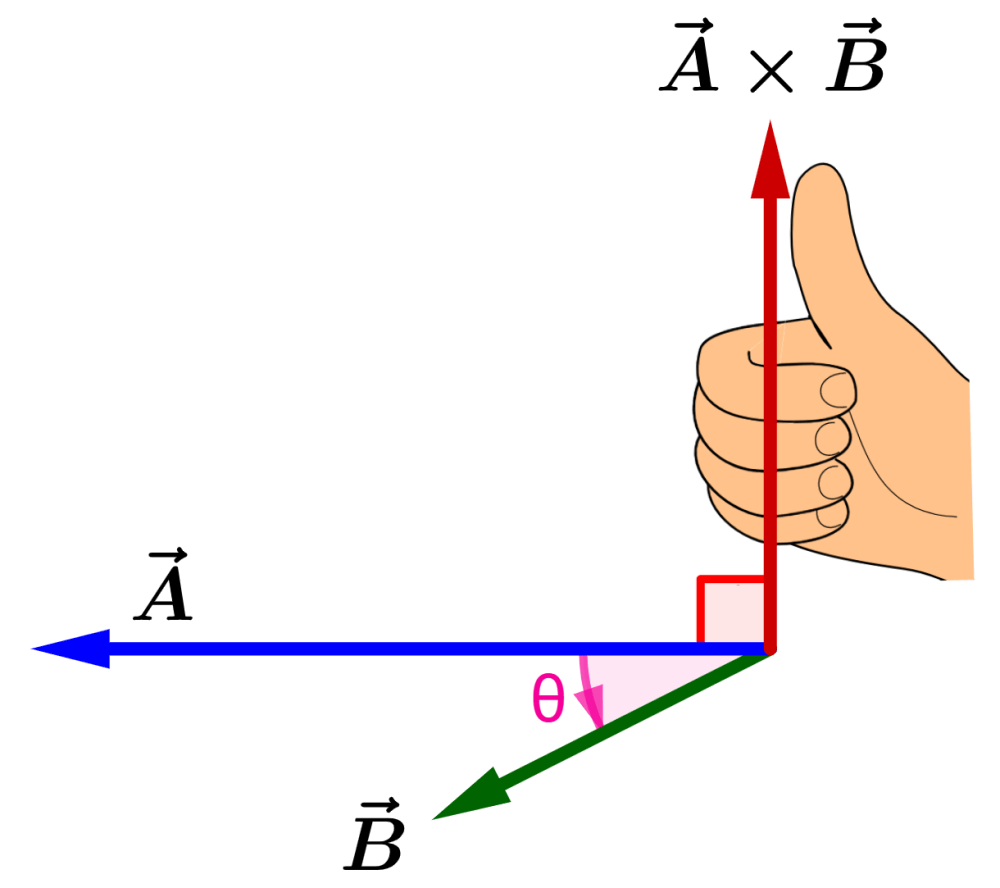
La dirección de $latex \vec{A}\times \vec{B}$ corresponde a la dirección hacia la cual apunta nuestro dedo pulgar.
De igual forma podemos encontrar la dirección de $latex \vec{B}\times \vec{A}$ al rotar desde el vector $latex \vec{A}$ hasta la dirección del vector $latex \vec{B}$, como se muestra en la figura:
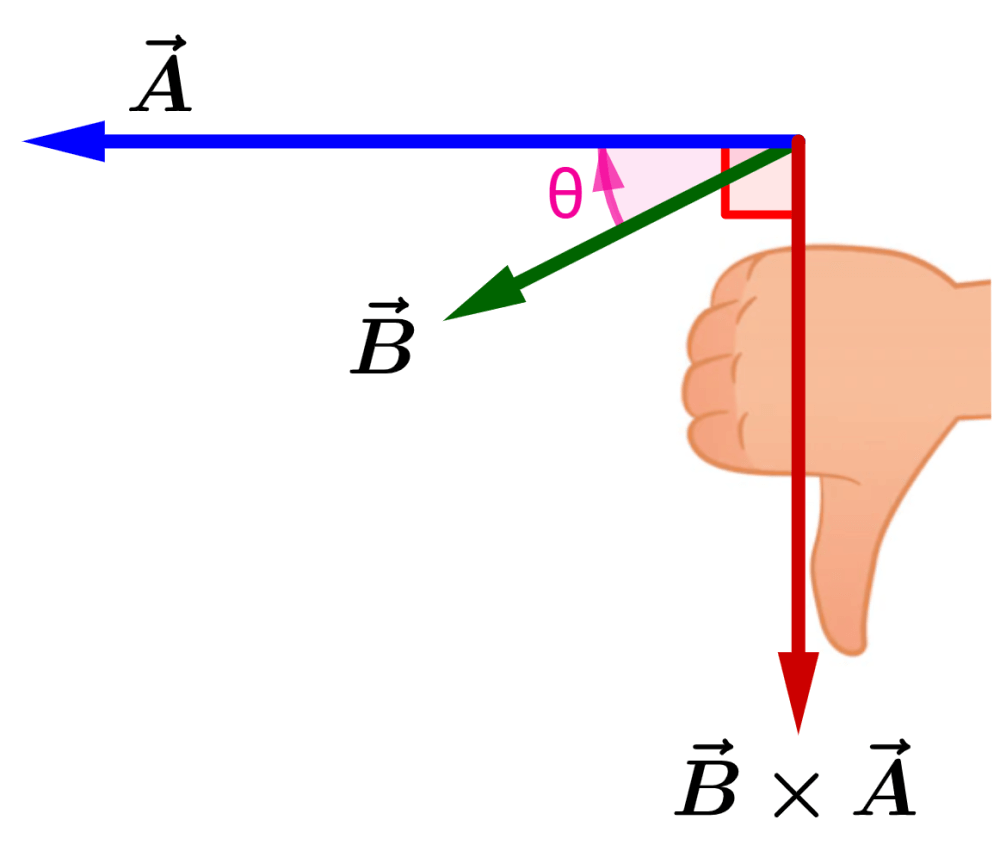
Vemos que $latex \vec{B}\times \vec{A}$ es opuesto a $latex \vec{A}\times \vec{B}$. Es decir, tenemos:
$latex \vec{A}\times \vec{B}=-\vec{B}\times \vec{A}$
Producto vectorial de vectores usando sus componentes
Los componentes dl producto vectorial de dos vectores $latex \vec{A} \cdot \vec{B}$ puede ser calculado con la siguiente fórmula si es que conocemos los componentes $latex x,~y,~z$ de los vectores:
$latex C_{x}=A_{y}B_{z}-A_{z}B_{y}$
$latex C_{y}=A_{z}B_{x}-A_{x}B_{z}$
$latex C_{z}=A_{x}B_{y}-A_{y}B_{x}$
Para demostrar esta fórmula, tenemos que encontrar el producto vectorial de los vectores unitarios $latex \hat{i},~\hat{j},~\hat{k}$.
El producto vectorial de cualquier vector por sí mismo es 0, entonces:
$latex \hat{i}\cdot \hat{i}=\hat{j}\cdot \hat{j}=\hat{k}\cdot \hat{k}=0$
Ahora, usamos la regla de la mano derecha para encontrar:
$latex \hat{i}\cdot \hat{j}=-\hat{j}\cdot \hat{i}=\hat{k}$
$latex \hat{j}\cdot \hat{k}=-\hat{k}\cdot \hat{j}=\hat{i}$
$latex \hat{k}\cdot \hat{i}=-\hat{i}\cdot \hat{k}=\hat{j}$
Ahora, escribimos a los vectores en términos de sus componentes, expandimos el producto y aplicamos los resultados encontrados arriba para simplificar:
$$\vec{A}\times \vec{B}=(A_{x}\hat{i}+A_{y}\hat{j}+A_{z}\hat{k})\times (B_{x}\hat{i}+B_{y}\hat{j}+B_{z}\hat{k})$$
$$=A_{x}\hat{i}\times B_{x}\hat{i}+A_{x}\hat{i}\times B_{y}\hat{j}+A_{x}\hat{i}\times B_{z}\hat{k})$$
$$+A_{y}\hat{j}\times B_{x}\hat{i}+A_{y}\hat{j}\times B_{y}\hat{j}+A_{y}\hat{j}\times B_{z}\hat{k})$$
$$+A_{z}\hat{k}\times B_{x}\hat{i}+A_{z}\hat{k}\times B_{y}\hat{j}+A_{z}\hat{k}\times B_{z}\hat{k})$$
Aquí, podemos reescribir a los términos individuales como $latex A_{x}\hat{i}\times B_{y}\hat{j}=A_{x}B_{y}\hat{i}\times\hat{j}$ y así. Al reagrupar y simplificar, tenemos:
$latex \vec{A}\times \vec{B}=(A_{y}B_{z}-A_{z}B_{y})\hat{i}+(A_{z}B_{x}-A_{x}B_{z})\hat{j}+(A_{x}B_{y}-A_{y}B_{x})\hat{k}$
Propiedades del producto vectorial de vectores
Las propiedades más importantes del producto vectorial de vectores son las siguientes:
Ortogonalidad
El resultado del producto cruz es un vector ortogonal (perpendicular) a los dos vectores de entrada. Si $latex \vec{C}= \vec{A} \times \vec{B}$, entonces el producto punto de $latex \vec{C}$ con $latex \vec{A}$ o $latex \vec{B}$ será cero, es decir,
$latex \vec{C}\cdot \vec{A} = 0$
y
$latex \vec{C}\cdot \vec{B} = 0$
No conmutatividad
El producto vectorial no es conmutativo, lo que significa que el orden de los vectores sí importa. Para dos vectores $latex \vec{A}$ y $latex \vec{B}$, $latex \vec{A} \times \vec{B}$ no es igual a $latex \vec{B} \times \vec{A}$. De hecho,
$latex \vec{A} \times \vec{B} = – \vec{B} \times \vec{A}$
Distributividad
El producto vectorial es distributivo sobre la suma de vectores. Es decir, tenemos
$latex \vec{A} \times (\vec{B} + \vec{C}) = (\vec{A} \times \vec{B}) + (\vec{A} \times \vec{C})$
Multiplicación escalar
El producto vectorial es compatible con la multiplicación escalar. Si $latex \vec{A}$ y $latex \vec{B}$ son vectores y $latex k$ es un escalar, entonces
$latex k(\vec{A} \times \vec{B}) = (k\vec{A}) \times \vec{B} = \vec{A} \times (k\vec{B})$
Vectores paralelos
Si dos vectores $latex \vec{A}$ y $latex \vec{B}$ son paralelos o antiparalelos, su producto vectorial será el vector cero (0, 0, 0).
Producto vectorial de un vector por sí mismo
De la anterior propiedad, sigue que el producto de un vector por sí mismo es igual a 0:
$latex \vec{A}\times \vec{A}=0$
Regla de la mano derecha
La dirección del producto vectorial se puede determinar usando la regla de la mano derecha. Si apunta con el dedo índice de la mano derecha en la dirección del primer vector ($latex \vec{A}$) y el dedo medio en la dirección del segundo vector ($latex \vec{B}$), el pulgar apuntará en la dirección del producto vectorial ($latex \vec{A} \times \vec{B}$).
Producto escalar triple
Dados tres vectores $latex \vec{A},~ \vec{B}~$ y $latex ~\vec{C}$, el producto escalar triple se define como el producto vectorial de $latex \vec{A}$ con el producto escalar de $latex \vec{B}~$ y $latex ~\vec{C}$, es decir, $latex \vec{A} \times \vec{B} \cdot \vec{C}$.
Esta cantidad es igual al volumen del paralelepípedo formado por los tres vectores y tiene la propiedad de que
$latex \vec{A} \times \vec{B} \cdot \vec{C}=\vec{B} \times \vec{C} \cdot \vec{A}=\vec{C} \times \vec{A} \cdot \vec{B}$
Prueba de colinealidad
Si $latex \vec{A} \times \vec{B} = 0$ y al menos uno de los vectores es distinto de cero, entonces $latex \vec{A}~$ y $latex ~\vec{B}$ son colineales, es decir, se encuentran en la misma línea en el plano.
Véase también
¿Interesado en aprender más sobre vectores? Puedes visitar las siguientes páginas.
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
