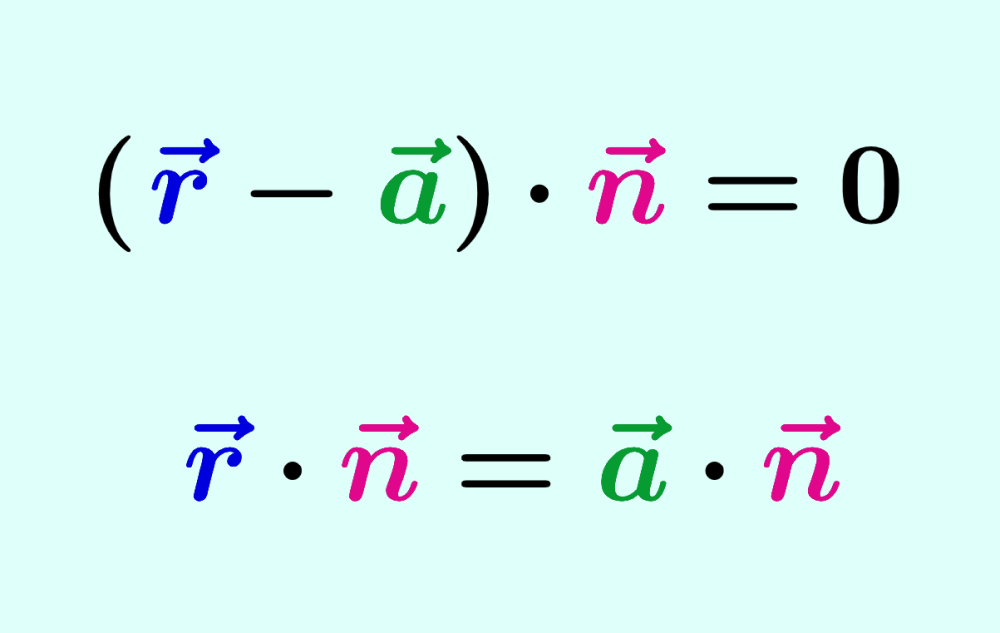La ecuación vectorial de un plano nos permite describir la posición de cada punto de un plano. Existen dos métodos principales para describir a un plano, con un punto en el plano y un vector perpendicular al plano o con tres puntos en el plano.
A continuación, conoceremos cómo encontrar la ecuación vectorial del plano usando los dos métodos mencionados. Luego, veremos algunos ejercicios en donde aplicaremos estos casos.
¿Cómo encontrar la ecuación vectorial de un plano?
Para encontrar la ecuación vectorial de un plano, podemos usar dos métodos principales dependiendo en la información que tengamos:
- Un punto en el plano y un vector perpendicular al plano
- Tres puntos en el plano que no se ubican en una línea recta
Primer caso
Empezamos con un punto $latex A $ y un vector $latex \vec{n}$, el cual es normal (perpendicular) al plano:
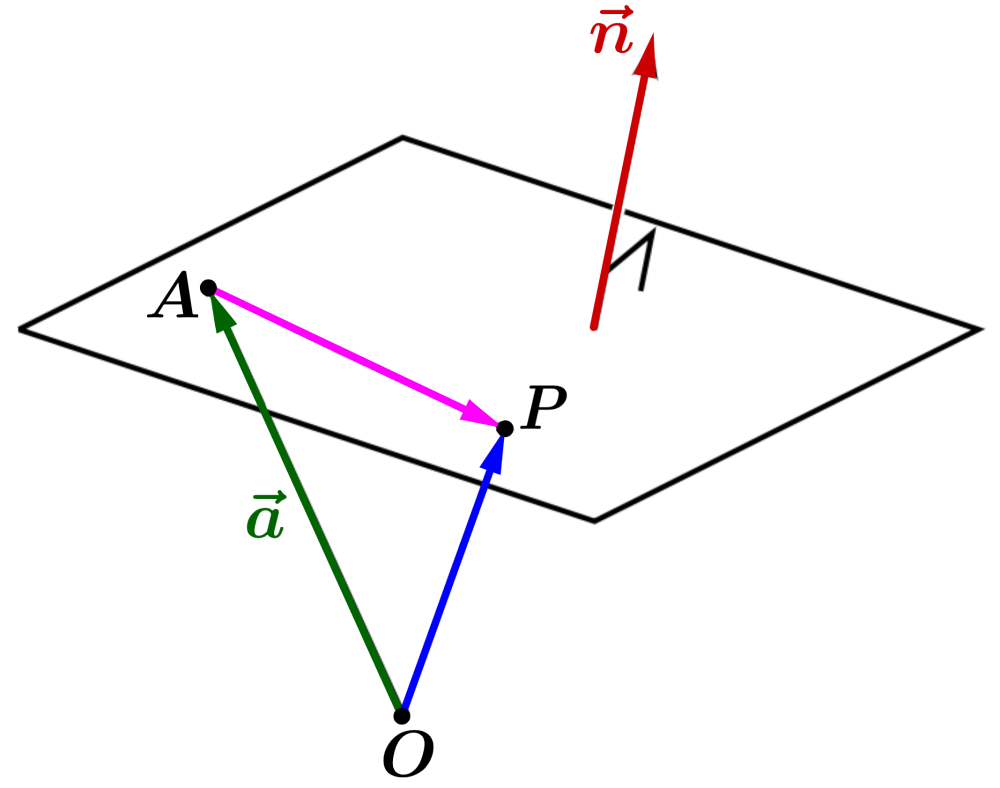
Cada vector paralelo al plano es perpendicular a $latex \vec{n}$. Esto significa que si es que cualquier punto $latex P $ está en el plano, debemos tener:
$latex \overrightarrow{AP}\cdot \vec{n}=0$
(el producto punto de dos vectores perpendiculares es 0)
En el diagrama, observamos que $latex \vec{r}$ es la suma de $latex \vec{a}$ y $latex \overrightarrow{AP}$. Entonces, tenemos $latex \overrightarrow{AP}=\vec{r}-\vec{a}$, por lo que la ecuación del plano es:
$latex \overrightarrow{AP}\cdot \vec{n}=0$
$latex (\vec{r}-\vec{a})\cdot \vec{n}=0$
Esto también puede ser escrito como $latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$.
Para convertir a coordenadas cartesianas, podemos usar $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$.
Segundo caso
En este caso, supongamos que tenemos tres puntos que se ubican en el plano y no son parte de la misma línea recta.
Podemos usar el producto vectorial para crear un vector ortogonal (perpendicular) al plano y proceder con el mismo proceso usado en el primer caso.
Por ejemplo, si es que sabemos que los puntos A, B y C se ubican en el plano, podemos escribir:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
Luego, usamos la ecuación $latex (\vec{r}-\vec{a})\cdot \vec{n}=0$.
Ejercicios resueltos de ecuación vectorial de un plano
EJERCICIO 1
Encuentra la ecuación del plano que pasa a través del punto $latex A(1, ~0,~2)$ y en el cual, $latex \vec{n}=\hat{i}-\hat{j}+\hat{k}$ es un vector perpendicular al plano.
Solución
Aquí, tenemos un punto en el plano y un vector perpendicular. Entonces, podemos usar la siguiente ecuación:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
En este caso, tenemos $latex \vec{a}=\hat{i}+2\hat{k}$, por lo que
$latex \vec{a}\cdot \vec{n}=1+0+2=3$
Además, dado que $latex \vec{n}=\hat{i}-\hat{j}+\hat{k}$, tenemos:
$latex \vec{r}\cdot \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}=3$
Para convertir a coordenadas cartesianas consideramos que $latex (x,~y,~z)$ son las coordenadas de cualquier punto $latex P$ en el plano.
Entonces, tenemos $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ y $latex \vec{r}\cdot \vec{n}=x-y+z$:
$latex \vec{r}\cdot \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}=3$
$latex x-y+z=3$
EJERCICIO 2
El punto $latex A(3, ~2,~1)$ se ubica en un plano y el vector $latex \vec{n}=2\hat{i}-2\hat{j}+\hat{k}$ es un vector perpendicular al plano. Encuentra la ecuación del plano.
Solución
Similar al ejercicio anterior, vamos a usar la siguiente fórmula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Dado que tenemos el vector posición $latex \vec{a}=3\hat{i}+2\hat{j}+\hat{k}$, podemos escribir:
$latex \vec{a}\cdot \vec{n}=6-4+1=3$
Como el vector perpendicular al plano es $latex \vec{n}=2\hat{i}-2\hat{j}+\hat{k}$, tenemos:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix}=3$
Usando $latex (x,~y,~z)$ como las coordenadas de un punto $latex P$ en el plano, tenemos $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ 1 \end{pmatrix}=3$
$latex 2x-2y+z=3$
EJERCICIO 3
Dado un punto $latex A(5,~ -2,~ 3)$ en un plano y el vector perpendicular $latex \vec{n} = 2\hat{i} -3\hat{j} +1\hat{k}$, encuentra la ecuación del plano.
Solución
Vamos a usar la siguiente fórmula para encontrar la ecuación del plano:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Dado que tenemos el vector posición $latex \vec{a}=5\hat{i}-2\hat{j}+3\hat{k}$, podemos escribir:
$latex \vec{a}\cdot \vec{n}=10+6+3=19$
Usando el vector perpendicular $latex \vec{n}=2\hat{i}-3\hat{j}+\hat{k}$, tenemos:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}=19$
Usamos $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ para escribir en coordenadas cartesianas:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}=19$
$latex 2x-3y+z=19$
EJERCICIO 4
Encuentra la ecuación vectorial del plano que pasa por el punto A(-1, 3, 2) y en el cual, el vector $latex \vec{n} = 2\hat{i} -2\hat{j} -3\hat{k}$ es perpendicular.
Solución
Similar a los ejercicios anteriores, usamos la siguiente fórmula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
El vector posición del punto dado es $latex \vec{a}=-\hat{i}+3\hat{j}+2\hat{k}$. Entonces, tenemos:
$latex \vec{a}\cdot \vec{n}=-2-6-6=-14$
Usando el vector perpendicular $latex \vec{n}=2\hat{i}-2\hat{j}-3\hat{k}$, tenemos:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ -3 \end{pmatrix}=-14$
Usamos $latex \vec{r}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}$ para escribir en coordenadas cartesianas:
$latex \vec{r}\cdot \begin{pmatrix} 2 \\ -2 \\ -3 \end{pmatrix}=-14$
$latex 2x-2y-3z=-14$
EJERCICIO 5
Encuentra la ecuación del plano que pasa a través de los puntos A(1, 1, 1), B(2, 1, 0) y C(1, 2, −1).
Solución
En los anteriores ejercicios, vimos cómo encontrar la ecuación del plano cuando tenemos un punto y un vector perpendicular $latex \vec{n}$.
Entonces, tenemos que encontrar un vector $latex \vec{n}$. Para esto podemos considerar que el vector perpendicular es igual al producto vectorial de dos vectores:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(\hat{i}-\hat{k})\times (\hat{j}-2\hat{k})$
$latex \vec{n}=\hat{i}+2\hat{j}+\hat{k}$
Ahora, usamos la siguiente fórmula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
El vector posición de A es $latex \vec{a}=\hat{i}+\hat{j}+\hat{k}$. Entonces, tenemos:
$latex \vec{a}\cdot \vec{n}=1+2+1=4$
y la ecuación es
$latex \vec{r}\cdot \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}=4$
en forma cartesiana, tenemos:
$latex x+2y+z=4$
EJERCICIO 6
Dados los puntos $latex A(1,~ 2,~ 3)$, $latex B(2, ~1, ~0)$, y $latex C(0,~ 3,~ 1)$, ¿cuál es la ecuación vectorial del plano que pasa por estos puntos?
Solución
Para encontrar el vector perpendicular $latex \vec{n}$, usamos lo siguiente:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(\hat{i}-\hat{j}-3\hat{k})\times (-\hat{i}+\hat{j}-2\hat{k})$
$latex \vec{n}=5\hat{i}+5\hat{j}$
Ahora, usamos la fórmula de la ecuación vectorial de un plano:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Podemos usar cualquiera de los puntos. El vector posición de A es $latex \vec{a}=\hat{i}+2\hat{j}+3\hat{k}$. Entonces, tenemos:
$latex \vec{a}\cdot \vec{n}=5+10+0=15$
y la ecuación del plano es
$latex \vec{r}\cdot \begin{pmatrix} 5 \\ 5 \\ 0 \end{pmatrix}=15$
en forma cartesiana, tenemos:
$latex 5x+5y=15$
EJERCICIO 7
Si un plano pasa por los puntos $latex A(2,~ 0, ~1)$, $latex B(0,~ 3,~ -1)$, y $latex C(1,~ -1,~ 3)$, ¿cuál es su ecuación vectorial?
Solución
Empezamos encontrando el vector perpendicular $latex \vec{n}$ usando el producto vectorial:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(-2\hat{i}+3\hat{j}-2\hat{k})\times (-\hat{i}-\hat{j}+2\hat{k})$
$latex \vec{n}=4\hat{i}+6\hat{j}+5\hat{k})$
Ahora, podemos aplicar la fórmula de la ecuación vectorial de un plano:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
El vector posición de A es $latex \vec{a}=2\hat{i}+\hat{k}$. Entonces, tenemos:
$latex \vec{a}\cdot \vec{n}=8+0+5=13$
y la ecuación del plano es
$latex \vec{r}\cdot \begin{pmatrix} 4 \\ 6 \\ 5 \end{pmatrix}=13$
en forma cartesiana, tenemos:
$latex 4x+6y+5z=13$
EJERCICIO 8
Encuentra la ecuación vectorial del plano que pasa por los puntos $latex A(1, ~1, ~1)$, $latex ~B(-1, ~2, ~0)$, y $latex C(2,~ 3,~ -1)$.
Solución
El vector perpendicular, $latex \vec{n}$, al plano es:
$latex \vec{n}=\overrightarrow{AB}~\times ~\overrightarrow{AC}$
$latex \vec{n}=(-2\hat{i}+\hat{j}-\hat{k})\times (\hat{i}+2\hat{j}-2\hat{k})$
$latex \vec{n}=-5\hat{j}-5\hat{k})$
Ahora, usamos la siguiente fórmula:
$latex \vec{r}\cdot \vec{n}=\vec{a}\cdot \vec{n}$
Usando el vector posición de A, $latex \vec{a}=\hat{i}+\hat{j}+\hat{k}$, tenemos:
$latex \vec{a}\cdot \vec{n}=0-5-5=-10$
y la ecuación del plano es
$latex \vec{r}\cdot \begin{pmatrix} 0 \\ -5 \\ -5 \end{pmatrix}=-10$
en forma cartesiana, tenemos:
$latex -5y-5z=-10$
Ecuación vectorial de un plano- Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
