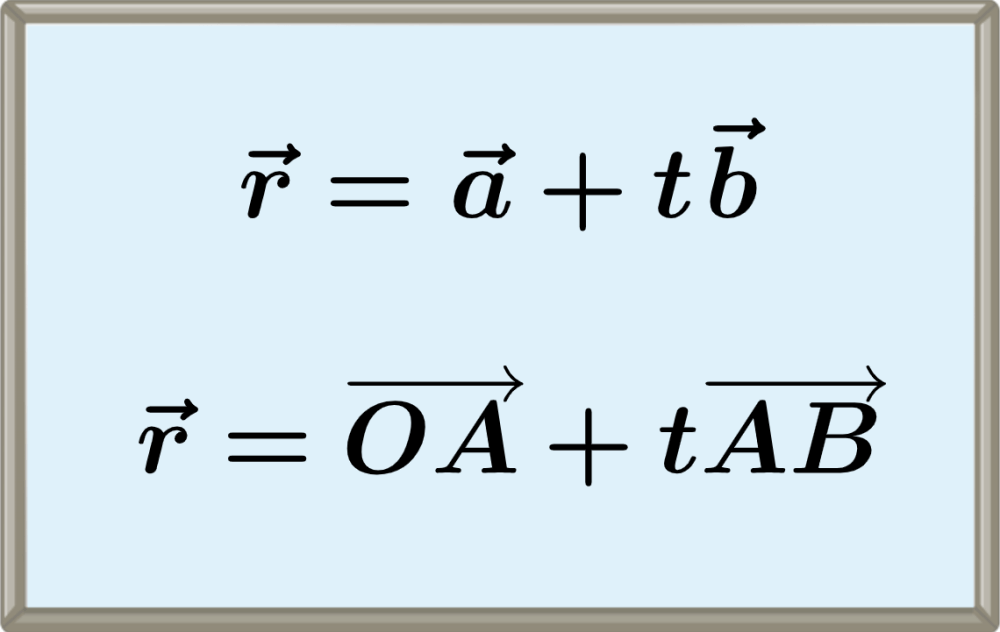La ecuación vectorial de una recta se utiliza para describir la posición de cada punto de una recta en términos de un único parámetro, normalmente denotado t. Podemos encontrar la ecuación vectorial de una recta si conocemos dos puntos en la recta o un punto y una dirección.
A continuación, aprenderemos a encontrar la ecuación vectorial de una recta usando ambos casos mencionados. Luego, veremos algunos ejercicios en donde aplicaremos estos casos.
¿Cómo encontrar la ecuación vectorial de una recta?
Existen dos métodos principales que podemos usar para encontrar la ecuación vectorial de una recta dependiendo en la información que tengamos disponible:
- Un punto en una recta y la dirección de la recta
- Dos puntos en la recta
Primer caso
Dado un punto $latex A $ y una dirección $latex \vec{u}$, podemos encontrar el vector posición $latex \vec{r}=\overrightarrow{OP}$ de un punto general $latex P$ en la recta:
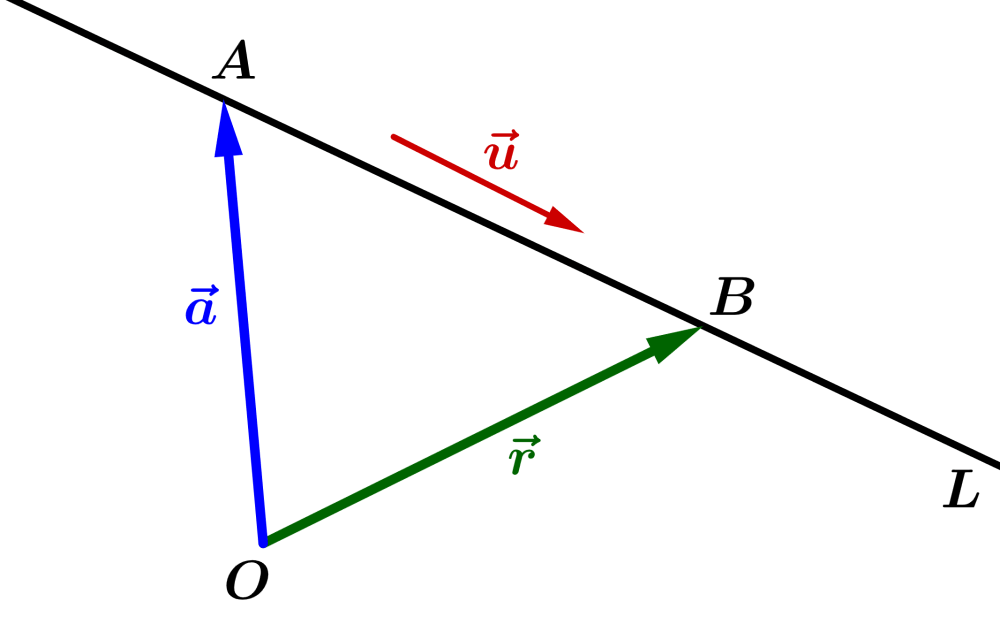
Usando la suma de vectores, podemos observar que:
$latex \overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{AP}$
Aquí tenemos $latex \vec{a}=\overrightarrow{OA}$ y dado que $latex \overrightarrow{AP}$ es paralelo a $latex =\vec{u}$, podemos escribir:
$latex \vec{r}=\vec{a}+t~\vec{u}$
en donde $latex t$ es un parámetro o cantidad escalar. En esta ecuación, diferentes valores de $latex t$ nos dan todos los puntos de la recta.
Segundo caso
Cuando conocemos dos puntos $latex A$ y $latex B$ en la recta, podemos expresar a la ecuación vectorial de la recta en términos de los vectores posición de los puntos.
Similar al caso anterior, tenemos $latex \vec{a}=\overrightarrow{OA}$. Además, en este caso, $latex \overrightarrow{AB}$ es paralelo a la recta, por lo que $latex \vec{u}=\overrightarrow{AB}$ y tenemos:
$latex \vec{r}=\overrightarrow{OA}+t~\overrightarrow{AB}$
Ejercicios resueltos de ecuación vectorial de la recta
EJERCICIO 1
Dados dos puntos A(1, 2, 3) y B(4, 6, 9), encuentra la ecuación vectorial de la recta que pasa por dichos puntos.
Solución
Para encontrar la ecuación vectorial de una recta, tenemos que empezar encontrar el vector posición de un punto de la recta ($latex \overrightarrow{OA}$) y el vector dirección ($latex \overrightarrow{AB}$) de la recta.
Dado que el punto $latex A$ tiene coordenadas $latex (1,~ 2,~ 3)$, y el punto $latex B$ tiene coordenadas $latex (4, ~6, ~9)$, su vector de posición será:
$$\overrightarrow{OA} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$$
$$\overrightarrow{OB} = \begin{pmatrix} 4 \\ 6 \\ 9 \end{pmatrix}$$
Ahora tenemos que encontrar el vector de dirección ($latex \vec{AB}$) de la recta. Esto se puede encontrar tomando la diferencia entre los vectores de posición de los puntos A y B:
$$\overrightarrow{AB} = \overrightarrow{OB}~ – ~\overrightarrow{OA}$$
$$\overrightarrow{AB} = \begin{pmatrix} 4 \\ 6 \\ 9 \end{pmatrix} – \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} 3 \\ 4 \\ 6 \end{pmatrix}$$
Ahora, podemos escribir la ecuación vectorial de la recta:
$latex \vec{r} = \overrightarrow{OA} + t~\overrightarrow{AB}$
$$\vec{r} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} + t \begin{pmatrix} 3 \\ 4 \\ 6 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 1+3t \\ 2+4t \\ 3+6t \end{pmatrix}$$
EJERCICIO 2
Dado un punto $latex C(2,~ -1,~ 4)$ en la recta y el vector dirección de la recta $latex \vec{d} = 4\hat{i}, ~5\hat{j}, ~-2\hat{k}$, encuentra la ecuación vectorial de la recta.
Solución
En este caso, conocemos el vector posición del punto C sobre la recta y el vector dirección ($latex \vec{d}$) de la recta.
El vector de posición del punto C con coordenadas $latex (2,~ -1, ~4)$ es:
$$\overrightarrow{OC} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix}$$
El vector de dirección de la recta está dado por:
$$\vec{d} = \begin{pmatrix} 4 \\ 5 \\ -2 \end{pmatrix}$$
Ahora, podemos escribir la ecuación vectorial de la recta:
$latex \vec{r} = \overrightarrow{OC}+ t~\vec{d}$
$$\vec{r} = \begin{pmatrix} 2 \\ -1 \\ 4 \end{pmatrix} + t \begin{pmatrix} 4 \\ 5 \\ -2 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 2+4t \\ -1+5t \\ 4-2t \end{pmatrix}$$
EJERCICIO 3
Dado un punto $latex A(5,~ -2,~ 3)$ en la recta y el vector dirección de la recta $latex \vec{e} = 2\hat{i} -3\hat{j} +1\hat{k}$, encuentra la ecuación vectorial de la recta.
Solución
Similar al ejercicio anterior, conocemos el vector posición del punto R sobre la recta y el vector dirección ($latex \vec{e}$) de la recta.
El vector de posición del punto A con coordenadas $latex (5,~ -2, ~3)$ es:
$$\overrightarrow{OA} = \begin{pmatrix} 5 \\ -2 \\ 3 \end{pmatrix}$$
Además, tenemos que el vector dirección de la recta es:
$$\vec{e} = \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$$
Entonces, podemos escribir a la ecuación vectorial de la recta usando esta información:
$latex \vec{r} = \overrightarrow{OA}+ t~\vec{e}$
$$\vec{r} = \begin{pmatrix} 5 \\ -2 \\ 3 \end{pmatrix} + t \begin{pmatrix} 2 \\ -3 \\ 1 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 5+2t \\ -2-3t \\ 3+t \end{pmatrix}$$
EJERCICIO 4
Encuentra la ecuación vectorial de la recta que pasa por los dos puntos P(-1, 3, 2) y Q(3, 7, -1).
Solución
Tenemos que empezar encontrando los vectores posición ($latex \overrightarrow{OP}$) y ($latex \overrightarrow{OQ}$).
Dado que el punto $latex P$ tiene coordenadas $latex (-1,~ 3,~ 2)$, y el punto $latex Q$ tiene coordenadas $latex (3, ~7, ~-1)$, tenemos:
$$\overrightarrow{OP} = \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix}$$
$$\overrightarrow{OQ} = \begin{pmatrix} 3 \\ 7 \\ -1 \end{pmatrix}$$
Ahora, vamos a encontrar el vector de dirección ($latex \vec{PQ}$) de la recta. Este vector es igual a la diferencia entre los vectores de posición de los puntos P y Q:
$$\overrightarrow{PQ} = \overrightarrow{OQ} ~-~ \overrightarrow{OP}$$
$$\overrightarrow{PQ} = \begin{pmatrix} 3 \\ 7 \\ -1 \end{pmatrix} – \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} 4 \\ 4 \\ -3 \end{pmatrix}$$
Ahora, podemos escribir la ecuación vectorial de la recta:
$latex \vec{r} = \overrightarrow{OP} + t~\overrightarrow{PQ}$
$$\vec{r} = \begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix} + t \begin{pmatrix} 4 \\ 4 \\ -3 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} -1+4t \\ 3+4t \\ 2-3t \end{pmatrix}$$
EJERCICIO 5
Dado un punto U(-3, 5, 2) sobre la recta y el vector dirección de la recta $latex \vec{f} = -1\hat{i}+ 4\hat{j} +3\hat{k}$, encuentra la ecuación vectorial de la recta.
Solución
Empezamos encontrando el vector posición del punto U con coordenadas $latex (-3,~ 5, ~2)$ es:
$$\overrightarrow{OU} = \begin{pmatrix} -3 \\ 5 \\ 2 \end{pmatrix}$$
En este caso, el vector dirección de la recta es:
$$\vec{f} = \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix}$$
Ahora, escribimos a la ecuación vectorial de la recta usando esta información:
$latex \vec{r} = \overrightarrow{OU}+ t~\vec{f}$
$$\vec{r} = \begin{pmatrix} -3 \\ 5 \\ 2 \end{pmatrix} + t \begin{pmatrix} -1 \\ 4 \\ 3 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} -3-t \\ 5+4t \\ 2+3t \end{pmatrix}$$
EJERCICIO 6
Dados dos puntos $latex S(6,~ 4,~ -1)$ y $latex T(0,~ -2, ~3)$, ¿cuál es la ecuación vectorial de la recta que pasa por estos puntos?
Solución
Los vectores posición ($latex \overrightarrow{OS}$) y ($latex \overrightarrow{OT}$) son:
$$\overrightarrow{OS} = \begin{pmatrix} 6 \\ 4 \\ -1 \end{pmatrix}$$
$$\overrightarrow{OT} = \begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix}$$
Ahora, vamos a encontrar el vector de dirección ($latex \vec{ST}$) de la recta:
$$\overrightarrow{ST} = \overrightarrow{OT} ~-~ \overrightarrow{OS}$$
$$\overrightarrow{ST} = \begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix} – \begin{pmatrix} 6 \\ 4 \\ -1 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} -6 \\ -6 \\ 4 \end{pmatrix}$$
Entonces, la ecuación vectorial de la recta es:
$latex \vec{r} = \overrightarrow{OS} + t~\overrightarrow{ST}$
$$\vec{r} = \begin{pmatrix} 6 \\ 4 \\ -1 \end{pmatrix} + t \begin{pmatrix} -6 \\ -6 \\ 4 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 6+-6t \\ 4-6t \\ -1+4t \end{pmatrix}$$
EJERCICIO 7
Encuentra la ecuación vectorial de la recta que pasa por los dos puntos A(1, 2, -1) y B(1, 1, 2) y determina si el punto P(1, 3, 1) está en la recta.
Solución
Los vectores posición de los puntos dados son:
$$\overrightarrow{OA} = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}$$
$$\overrightarrow{OB} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}$$
El vector de dirección ($latex \vec{AB}$) de la recta es:
$$\overrightarrow{AB} = \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} – \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix}$$
$$\overrightarrow{AB} = \begin{pmatrix} 0 \\ -1 \\ 3 \end{pmatrix}$$
Entonces, la ecuación vectorial de la recta es:
$latex \vec{r} = \overrightarrow{OA} + t~\overrightarrow{AB}$
$$\vec{r} = \begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + t \begin{pmatrix} 0 \\ -1 \\ 3 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} 1 \\ 2-t \\ -1+3t \end{pmatrix}$$
Para determinar si P está en la recta, tenemos que encontrar el valor de $latex t$. Comparando los componentes de la ecuación vectorial y la posición del punto, tenemos:
$latex 1=1$
$latex 2-t=3~~(t=-1)$
$latex -1+3t=1~~(t=\frac{2}{3})$
Las dos últimas ecuaciones no son compatibles, por lo que el punto P no está en la recta.
EJERCICIO 8
Encuentra las ecuaciones vectoriales de las rectas $latex \overrightarrow{AB}~$ y $latex ~\overrightarrow{CD}$, con los puntos $latex A(1, ~2,~ -1)$, $latex B(1, ~1,~ 2)$, $latex C(0, ~1, ~2)~$ y $latex ~D(-1,~ 3,~ -4)$.
Encuentra el punto de intersección de las rectas.
Solución
La ecuación vectorial para ($latex \overrightarrow{AB}$) fue encontrada en el ejercicio anterior. Entonces, tenemos:
$$\vec{r} = \begin{pmatrix} 1 \\ 2-t \\ -1+3t \end{pmatrix}$$
La recta $latex \overrightarrow{CD}$ está dada por $latex \vec{r}=\overrightarrow{OC}+s~\overrightarrow{CD}$. Entonces, tenemos:
$$\vec{r} = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} + s \begin{pmatrix} -1 \\ 2 \\ -6 \end{pmatrix}$$
$$\vec{r} = \begin{pmatrix} -s\\ 1+2s \\ 2-6s \end{pmatrix}$$
Las rectas $latex \overrightarrow{AB}~$ y $latex ~\overrightarrow{CD}$ intersecan si es que los parámetros $latex s$ y $latex t$ cumplen con lo siguiente:
$$ \begin{pmatrix} 1 \\ 2-t \\ -1+3t \end{pmatrix} = \begin{pmatrix} -s\\ 1+2s \\ 2-6s \end{pmatrix}$$
De la primera fila, tenemos $latex 1=-s$. Entonces, para que las rectas se intersequen, debemos tener $latex s=-1$.
De la segunda fila:
$latex 2 − t = 1 + 2s$
$latex 2 − t = −1$
$latex t = 3$
Sustituyendo $latex s=-1$ y $latex t=3$ en la tercera fila $latex −1 + 3t = 2 − 6s$, resulta $latex 8 = 8$. Entonces, los valores de $latex s$ y $latex t$ satisfacen las tres ecuaciones.
El punto de intersección es encontrado al sustituir $latex s=-1$ o $latex t=3$ en $latex \overrightarrow{AB}~$ o $latex ~\overrightarrow{CD}$ respectivamente.
El punto de intersección es $latex (1,~ −1, ~8)$.
Ecuación vectorial de la recta – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre vectores? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
