El triángulo de Pascal es un tipo de patrón de números. Los números están organizados en una manera que reflejan a un triángulo. Primero, el 1 es colocado en la parte superior. Luego, el resto de números son colocados en un patrón triangular. Los números que obtenemos en cada paso son la suma de los dos números encima del número. Este es un concepto similar a los números triangulares.
A continuación, haremos una revisión de lo que es el triángulo de Pascal y aprenderemos a construirlo. Además, conoceremos las propiedades fundamentales del triángulo de Pascal.
ÁLGEBRA
Relevante para…
Conocer las propiedades fundamentales del triángulo de Pascal.
ÁLGEBRA

Relevante para…
Conocer las propiedades fundamentales del triángulo de Pascal.
Definición del triángulo de Pascal
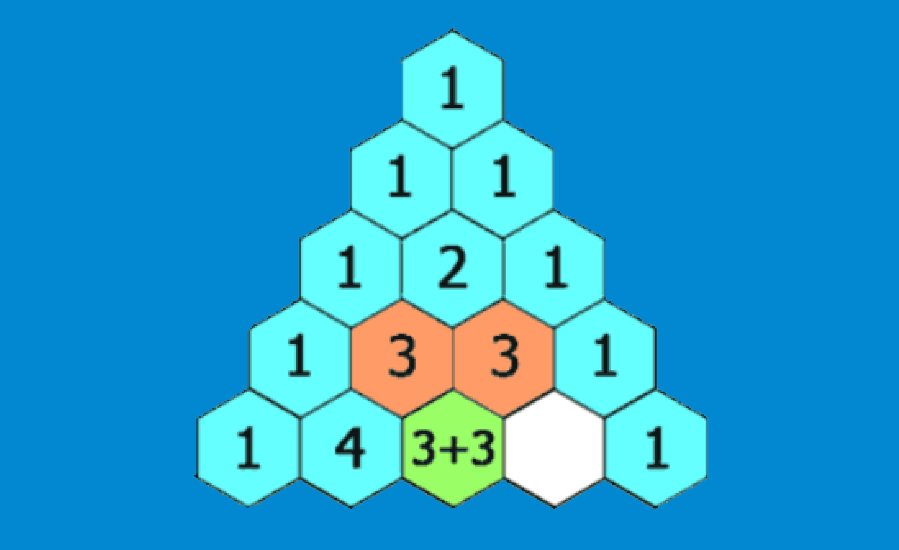
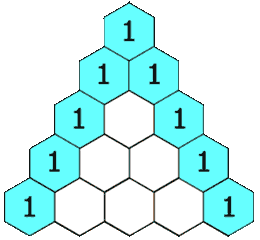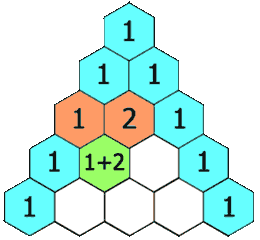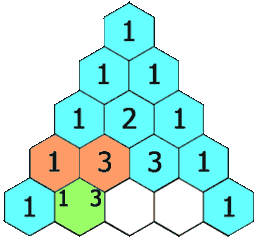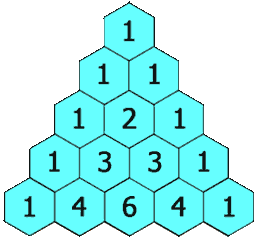
El triángulo de Pascal puede ser introducido a través de un conjunto de reglas. Para formar el triángulo de Pascal, empezamos con el 1 en la parte superior y ubicamos a «1» a lo largo de los dos lados del triángulo.
Cada número nuevo se ubicará entre dos números y debajo de ellos, y su valor es igual a la suma de esos dos números. El triángulo teórico es infinito y puede continuar indefinidamente hasta que sea necesario.
Construcción del triángulo de Pascal
Las filas en el triángulo de Pascal son enumeradas empezando desde el 0, por lo que la fila de la parte superior es la fila 0. La forma más fácil de construir un triángulo de Pascal es empezar desde la fila cero y escribir solo el número 1.
Desde allí, obtenemos cada número en la siguiente fila al sumar los dos números que están directamente en la parte de arriba izquierda y derecha. Si es que no hay ningún número hacia la derecha o izquierda, reemplazamos un cero por ese número y procedimos con la adición.
La siguiente es una ilustración de cómo construir al triángulo de Pascal:
Propiedades del triángulo de Pascal
Las siguientes son las propiedades más importantes del triángulo de Pascal:
- Cada número es la suma de los dos números encima de él.
- Todos los números exteriores son iguales a 1.
- El triángulo de Pascal es simétrico.
- La primera diagonal muestra los números de conteo.
- Las sumas de las filas dan las potencias del 2.
- Cada fila da los dígitos de las potencias del 11.
- Cada elemento representa a la combinación $latex _{m}C_{n}$, en donde, m es la fila del elemento y n es la posición del elemento en la fila.
- Cada fila representa a los coeficientes binomiales.
- Los números Fibonacci están a lo largo de las diagonales.
Patrones del triángulo de Pascal
Suma de las filas
Una de las propiedades interesantes del triángulo es que la suma de los números en una fila es igual a $latex {{2}^n}$, en donde, n corresponde al número de la fila. Por ejemplo, tenemos:
- $latex 1=1={{2}^0}$
- $latex 1+1=2={{2}^1}$
- $latex 1+2+1=4={{2}^2}$
- $latex 1+3+3+1=8={{2}^3}$
- $latex 1+4+6+4+1=16={{2}^4}$
Números primos en el triángulo
Otro patrón visible en el triángulo se relaciona a los números primos. Si es que una fila empieza con un número primo o es una fila con número primo, todos los números que están en esa fila, sin incluir al 1, son divisibles para ese número primo.
Si es que miramos a la fila 5 (1, 5, 10, 10, 5, 1) podemos ver que el 5 y el 10 son divisibles por 5. Sin embargo, para una fila compuesta como la fila 8 (1, 8, 28, 56, 70, 56, 28, 8, 1), 28 y 70 no son divisibles por 8.
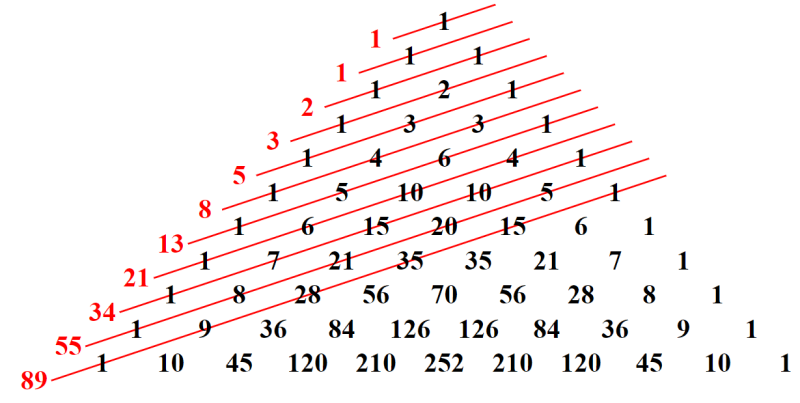
Sucesión de Fibonacci en el triángulo
Al sumar los números en las diagonales en el triángulo de Pascal, podemos obtener la sucesión de Fibonacci, tal como se muestra en la figura:
Expansión binomial con el triángulo de Pascal
El triángulo de Pascal define a los coeficientes que aparecen en las expresiones binomiales. Eso significa que la fila n del triángulo de Pascal contiene a los coeficientes de la expresión expandida del binomio $latex {{(x+y)}^n}$.
Los coeficientes de la expansión pueden ser expresados como $latex a_{k}=_{n}C_{k}$. Por ejemplo, podemos expandir la expresión para el binomio $latex {{x+y}^3}$:
$${{(x+y)}^3}=_{3}C_{0}{{x}^3}+_{3}C_{1}{{x}^2}y+_{3}C_{2}x{{y}^2}+_{3}C_{3}{{y}^3}$$
$latex =(1){{x}^3}+(3){{x}^2}y+(3)x{{y}^2}+(1){{y}^3}$
En esta expresión, tenemos $latex n=3$, lo que significa que usamos los números de la fila 3 del triángulo de Pascal, que son 1, 3, 3, 1.
Véase también
¿Interesado en aprender más sobre el triángulo de Pascal y el teorema del binomio? Mira estas páginas:


