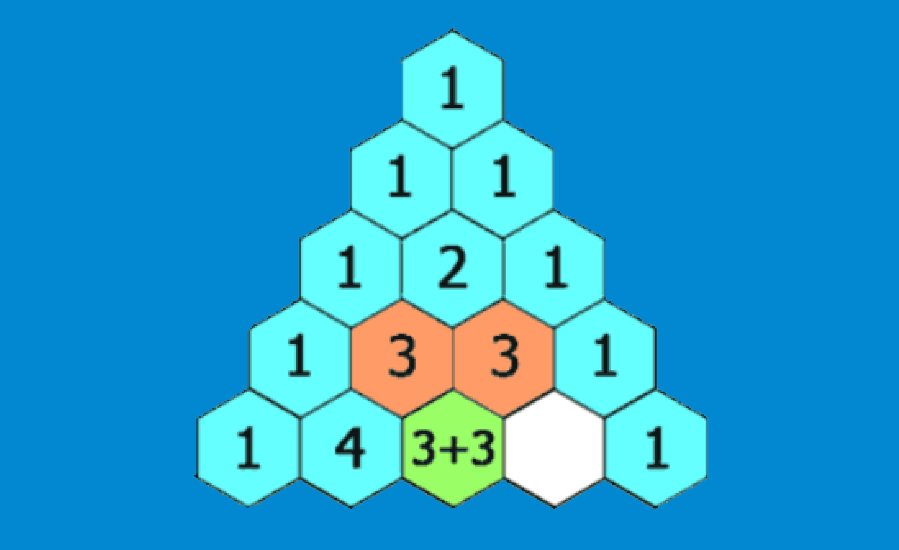
El triángulo de Pascal tiene muchas aplicaciones en matemáticas y estadística. Podemos usar el triángulo de Pascal para encontrar la expansión binomial. También, el triángulo de Pascal es usado en aplicaciones probabilísticas y en el cálculo de combinaciones. Recordemos que el triángulo de Pascal es un patrón de números en la forma de un triángulo, en donde cada número es encontrado sumando los dos números encima de él.
A continuación, miraremos cada una de las aplicaciones del triángulo de Pascal más importantes en detalle junto con algunos ejemplos para entender su uso.
ÁLGEBRA
Relevante para…
Conocer algunas de las aplicaciones del triángulo de Pascal.
ÁLGEBRA
Relevante para…
Conocer algunas de las aplicaciones del triángulo de Pascal.
Triángulo de Pascal en expansión binomial
El siguiente es el triángulo de Pascal:
Podemos usar las filas del triángulo de Pascal para facilitar el proceso de expansión binomial. De acuerdo con la potencia del binomio, podemos usar una fila del triángulo de Pascal que representa a los coeficientes de los valores expandidos. Usamos n+1 para determinar la fila que tenemos que usar, en donde, n representa a la potencia del binomio.
Alternativamente, podemos considerar a la primera fila como 0 y tomar a la fila del triángulo de Pascal indicada por la potencia. Por ejemplo, veamos la siguiente expansión binomial:
$latex {{(a+b)}^2}=1{{a}^2}+2ab+1{{b}^2}$
En esta expansión, tenemos los coeficientes 1, 2, 1. Esto corresponde a la tercera fila del triángulo de Pascal. Vemos que la potencia del binomio es 2, por lo que al usar n+1, tenemos 3 que sí corresponde con la tercera fila usada.
EJEMPLO
- Expande al binomio $latex {{(x+y)}^4}$.
Solución: En este caso la potencia es 4, por lo que tenemos que usar la fila $latex 4+1=5$. Esta fila corresponde a los números 1, 4, 6, 4, 1. Estos son los coeficientes de la expansión binomial y nos dice que tendremos 5 términos en la expansión. Además, sabemos que expandimos un binomio al empezar con cada término en la potencia más alta y reducir hasta llegar a 0, cada término en dirección opuesta:
$latex {{(x+y)}^4}$
$$=1{{x}^4}{{y}^0}+4{{x}^3}{{y}^1}+6{{x}^2}{{y}^2}+4{{x}^1}{{y}^3}+1{{x}^0}{{y}^4}$$
$$=1{{x}^4}(1)+4{{x}^3}{{y}^1}+6{{x}^2}{{y}^2}+4{{x}^1}{{y}^3}+1(1){{y}^4}$$
$latex ={{x}^4}+4{{x}^3}y+6{{x}^2}{{y}^2}+4x{{y}^3}+{{y}^4}$
Triángulo de Pascal en probabilidad
El triángulo de Pascal puede ser usado en probabilidad para simplificar el conteo de probabilidades de algún evento. Por ejemplo, el triángulo de Pascal puede mostrarnos en cuántas maneras podemos combinar caras y sellos en lanzamiento de monedas.
Luego, esto puede mostrarnos la probabilidad de cualquier combinación. En el siguiente ejemplo S representa sellos y C representa caras.
EJEMPLO
Supongamos que una moneda es lanzada 4 veces, las probabilidades de las combinaciones son:
- CCCC
- CCCS, CCSC, CSCC, SCCC
- CCSS, CSCS, CSSC, SCCS, SCSC, SSCC
- CSSS, SCSS, SSCS, SSSC
- SSSS
Entonces, el patrón observado es 1, 4, 6, 4, 1. Si es que estamos buscando el número total de posibilidades, solo tenemos que sumar los números. Es decir, tenemos $latex 1+4+6+4+1=16$ combinaciones posibles si es que lanzamos una moneda 4 veces.
Triángulo de Pascal en combinaciones
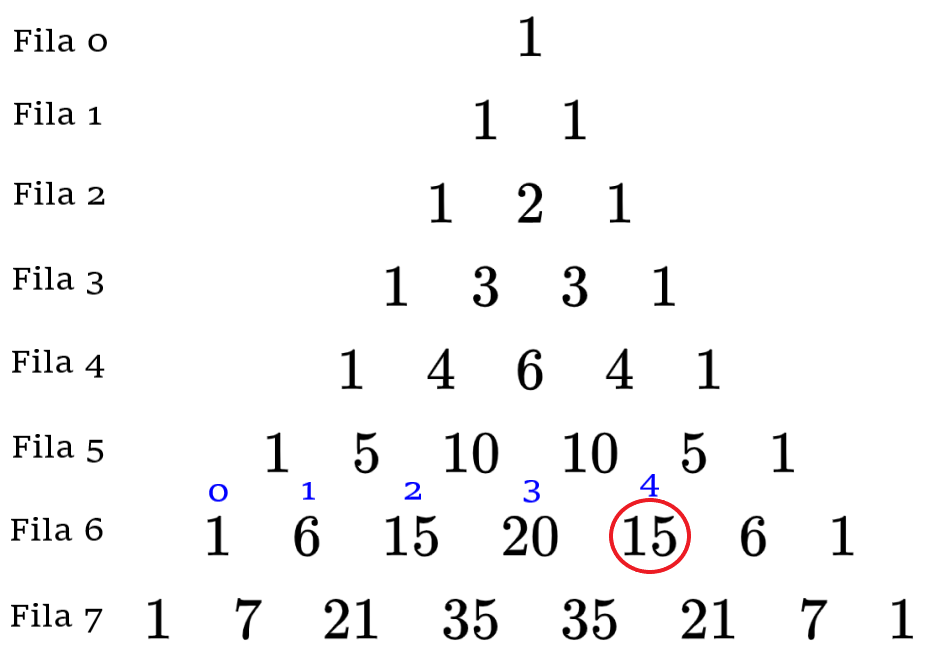
El triángulo de Pascal puede ser usado para encontrar combinaciones. La fila superior del triángulo de Pascal es la fila 0 y el primer número en cada fila es el elemento cero de esa fila.
Por ejemplo, si es que queremos encontrar la combinación $latex _{6}C_{4}$, tenemos que mirar a la fila 6 y al elemento 4. La respuesta es 15:
EJEMPLO
- Tenemos 5 canicas en una bolsa, 1 roja, 1 azúl, 1 verde, 1 amarilla y 1 negra. ¿Cuántas combinaciones son posibles si es que queremos sacar 2 canicas?
Soluciones: El número total de canicas es 5 y queremos escoger 2 canicas. Entonces, tenemos la combinación $latex _{5}C_{2}$. Esto significa que tenemos que mirar en el 2 elemento de la fila 5. Esto significa que la respuesta es 10.
Véase también
¿Interesado en aprender más sobre el triángulo de Pascal y el teorema del binomio? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
