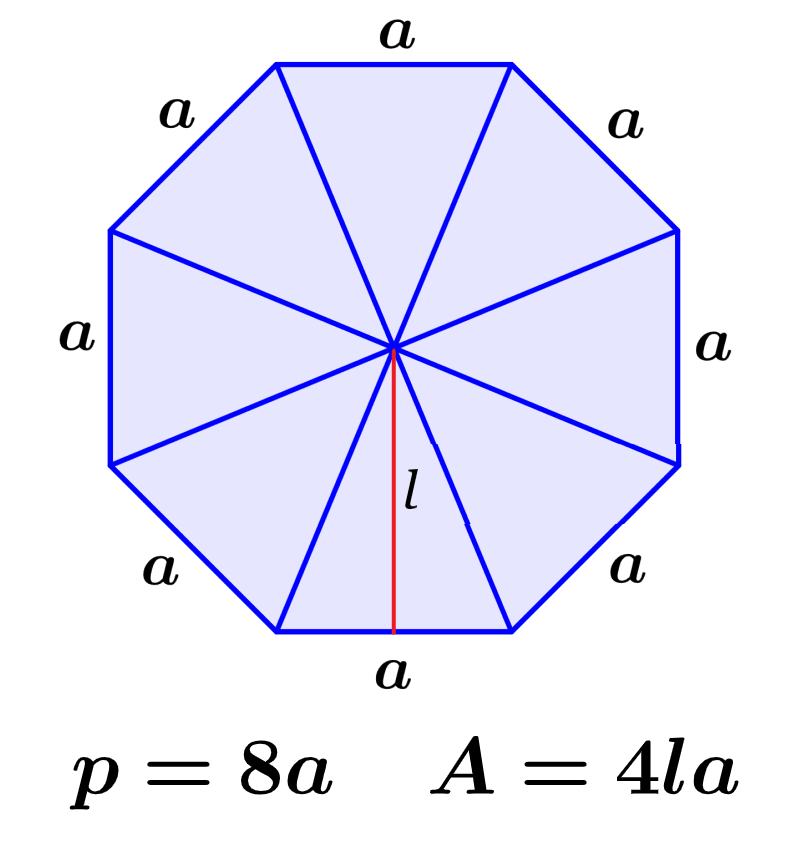
El perímetro de un octágono es la longitud total alrededor de su contorno. Por otro lado, el área es una medida del espacio bidimensional ocupado por la figura. Podemos calcular el perímetro del octágono al sumar las longitudes de sus ocho lados y podemos calcular su área al multiplicar por cuatro al producto de uno de sus lados y de su apotema.
A continuación, aprenderemos todo lo relacionado con el perímetro y el área de un octágono. Conoceremos sus fórmulas y las aplicaremos para resolver algunos ejercicios de práctica.
¿Cómo calcular el perímetro de un octágono?
Para calcular el perímetro de un octágono, tenemos que sumar las longitudes de sus ocho lados. Entonces, podemos usar la siguiente fórmula:
$$p=a+b+c+d+e+f+g+h$$
en donde, $latex a,~b,~c,~d,~e,~f,~g,~h$ son las ocho longitudes de los lados del octágono.
Además, si es que tenemos un octágono regular, sabemos que las longitudes de sus ocho lados son las mismas, por lo que podemos multiplicar a la longitud de uno de sus lados por ocho para encontrar el perímetro:
| $latex p=8a$ |
en donde, a es la longitud de uno de los lados del octágono regular.
¿Cómo calcular el área de un octágono?
Para calcular el área de un octágono, podemos multiplicar por 4 al producto de la longitud de uno de sus lados y de su apotema. Entonces, podemos usar la siguiente fórmula:
| $latex A=4la$ |
en donde, l es la longitud de uno de los lados del octágono y a es la longitud de la apotema.
Demostración de la fórmula del área de un octágono
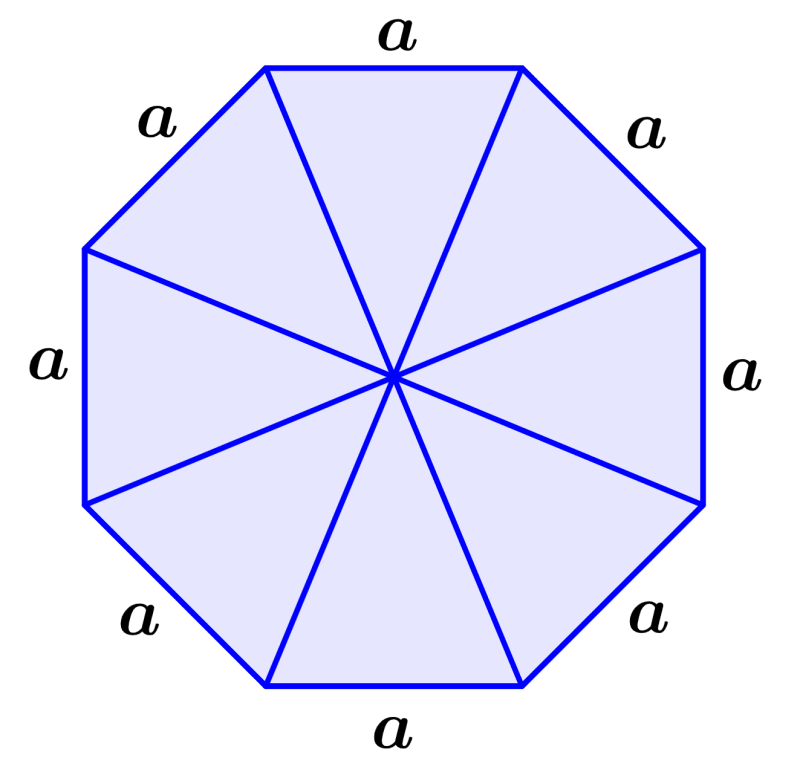
El área de cualquier polígono puede ser encontrada al dividirlo en triángulos congruentes y calcular el área de cada triángulo. En el caso de octágonos, podemos dividir a la figura en ocho triángulos congruentes, como se muestra a continuación:
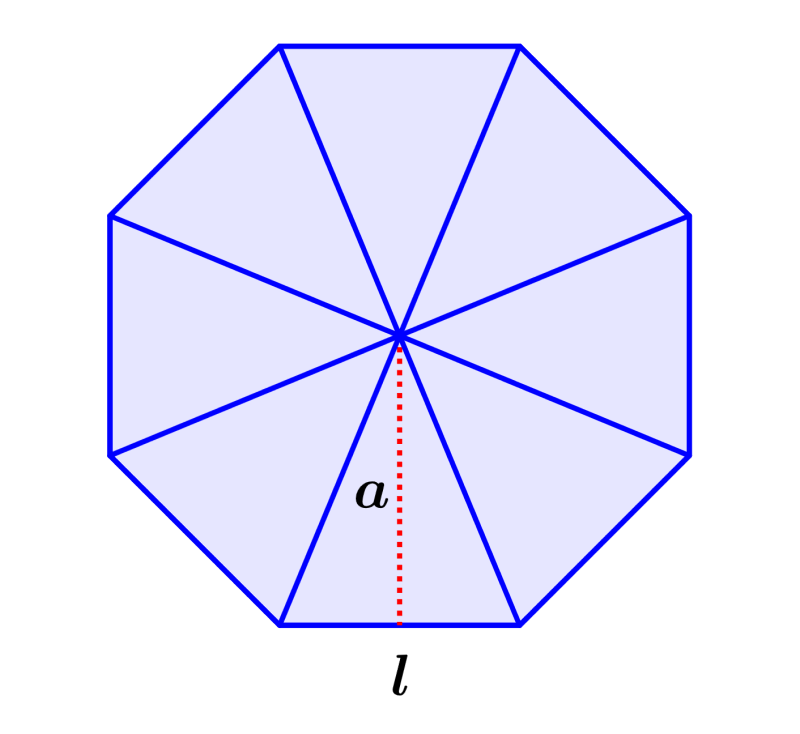
Ahora, recordamos que el área de cualquier triángulo puede ser calculada usando la fórmula $latex A=\frac{1}{2}bh$, en donde, b es la longitud de la base y h es la longitud de la altura.
En el diagrama, podemos observar que la altura del triángulo es igual a la apotema del octágono y la base del triángulo es igual a la longitud de uno de sus lados, por lo que tenemos $latex A=\frac{1}{2}la$.
Dado que tenemos ocho triángulos congruentes, podemos multiplicar por ocho para obtener la siguiente fórmula:
$latex A=4la$
Calcular el área de un octágono sin usar la apotema
Podemos calcular el área de un octágono regular sin usar la longitud de su apotema. Para esto, podemos obtener una fórmula del área de un octágono regular solo en términos de sus lados.
Usando trigonometría y simplificando, podemos encontrar la siguiente fórmula:
| $latex A=2(1+\sqrt{2}){{l}^2}$ |
en donde, l es la longitud de uno de los lados del octágono.
Área y perímetro de un octágono – Ejercicios resueltos
EJERCICIO 1
¿Cuál es el perímetro de un octágono regular que tiene lados con una longitud de 5 cm?
Solución
Al aplicar la fórmula del perímetro con la longitud $latex a=5$, tenemos:
$latex p=8a$
$latex p=8(5)$
$latex p=40$
El perímetro del octágono es igual 40 cm.
EJERCICIO 2
Encuentra el área de un octágono regular que tiene lados con una longitud de 5 mm y una apotema con una longitud de 6.04 mm
Solución
Tenemos las siguientes longitudes
- Lados, $latex l=5$ mm
- Apotema, $latex a=6.04$ mm
Usando estas longitudes en la fórmula del área, tenemos:
$latex A=4la$
$latex A=4(5)(6.04)$
$latex A=120.8$
El área del octágono es igual a 120.8 mm².
EJERCICIO 3
¿Cuál es el perímetro de un octágono regular que tiene lados con una longitud de 8 m?
Solución
Usando la longitud $latex a=8$ en la fórmula del perímetro del octágono, tenemos:
$latex p=8a$
$latex p=8(8)$
$latex p=64$
El perímetro del octágono es igual a 64 m.
EJERCICIO 4
Encuentra el área de un octágono regular que tiene lados con una longitud de 6 cm y una apotema de 7.24 cm.
Solución
Tenemos lo siguiente:
- Lados, $latex l=6$ cm
- Apotema, $latex a=7.24$ cm
Usando estas longitudes en la fórmula del área, tenemos:
$latex A=4la$
$latex A=4(6)(7.24)$
$latex A=173.76$
El área del octágono es igual a 173.76 cm².
EJERCICIO 5
Encuentra el perímetro de un octágono regular que tiene lados con una longitud de 15 mm.
Solución
Tenemos la longitud $latex a=15$. Usando este valor en la fórmula del perímetro, tenemos:
$latex p=8a$
$latex p=8(15)$
$latex p=120$
El perímetro del octágono es 120 m.
EJERCICIO 6
Encuentra el área de un octágono regular que tiene lados con una longitud de 11 m y una apotema con una longitud de 13.28 m.
Solución
Tenemos las siguientes longitudes:
- Lados, $latex l=11$ m
- Apotema, $latex a=13.28$ m
Al aplicar estos valores en la fórmula del área, tenemos:
$latex A=4la$
$latex A=4(11)(13.28)$
$latex A=584.32$
El área del octágono es igual a 584.32 m².
EJERCICIO 7
Calcula la longitud de los lados de un octágono regular que tiene un perímetro de 112 cm.
Solución
En esta caso, conocemos el perímetro del octágono y queremos encontrar la longitud de los lados del octágono. Entonces, usamos la fórmula del perímetro y resolvemos para a:
$latex p=8a$
$latex 112=8a$
$latex a=14$
La longitud de los lados del octágono es 14 cm.
EJERCICIO 8
Calcula el área de un octágono regular que tiene lados con una longitud de 8 m.
Solución
En este caso, solo tenemos la longitud de un lado del octágono, por lo que podemos usar la segunda fórmula del área con $latex l=8$:
$latex A=2(1+\sqrt{2}){{l}^2}$
$latex A=2(1+\sqrt{2}){{(8)}^2}$
$latex A=2(1+\sqrt{2})(64)$
$latex A=309.02$
El área del octágono es igual a 309.02 m².
EJERCICIO 9
¿Cuál es la longitud de los lados de un octágono regular que tiene un perímetro de 152 mm?
Solución
Usando la fórmula del perímetro con $latex p=152$ y resolviendo para a, tenemos:
$latex p=8a$
$latex 152=8a$
$latex a=19$
La longitud de los lados del octágono es igual a 19 mm.
EJERCICIO 10
Calcula el área de un octágono regular que tiene lados con una longitud de 10 m.
Solución
Podemos usar la segunda fórmula del área con $latex l=10$:
$latex A=2(1+\sqrt{2}){{l}^2}$
$latex A=2(1+\sqrt{2}){{(10)}^2}$
$latex A=2(1+\sqrt{2})(100)$
$latex A=482.84$
El área del octágono es igual a 482.84 m².
Área y perímetro de un octágono – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre perímetros y áreas de figuras geométricas? Puedes mirar estas páginas: