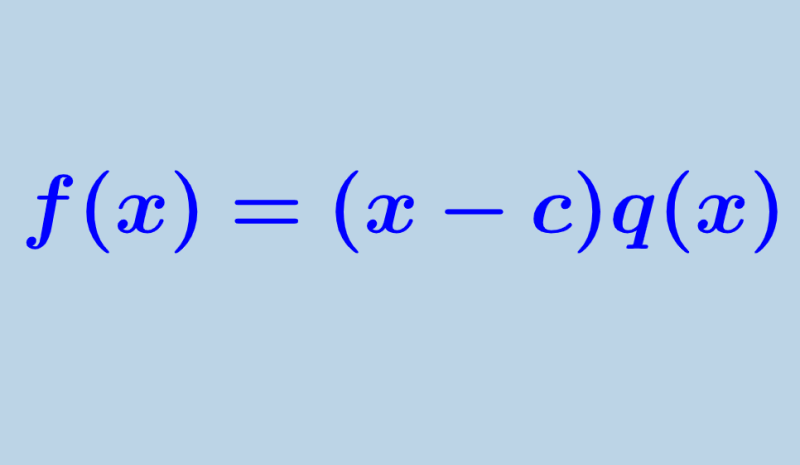El teorema del factor se usa con frecuencia para factorizar un polinomio y encontrar sus raíces. El teorema del residuo polinomial es un ejemplo de esto. El teorema del factor se puede utilizar como técnica de factorización de polinomios.
En este artículo, veremos una demostración del teorema del factor, así como ejemplos con respuestas y problemas de práctica.
Resumen del teorema del factor
El teorema del factor nos permite factorizar cualquier polinomio probando diferentes factores posibles. Básicamente nos dice que, si (x-c) es un factor de un polinomio, entonces debemos tener f(c)=0.
Podemos probar el teorema del factor considerando que el resultado de dividir un polinomio f(x) entre (x-c) es f(c)=0. Por lo tanto, podemos escribir:
$latex f(x)= (x-c)q(x)+f (c)$
f(x) es el polinomio objetivo, mientras que q(x) es el polinomio cociente.
Podemos usar el hecho de que f(c)=0, para obtener:
$latexf(x)= (x-c)q(x)+f (c)$
$latexf(x) = (x-c)q(x)+0$
$latexf(x) = (x-c)q (x)$
Como resultado, (x-c) es un factor del polinomio f(x).
Las siguientes afirmaciones se aplican a cualquier polinomio f(x):
- El resto es cero cuando f(x) se divide exactamente por (x–c)
- (x-c) es un factor de f(x)
- c es la solución de f(x)
- c es un cero de la función f(x), o f(c)=0
Ejercicios de teorema del factor resueltos
Usando la fórmula detallada anteriormente, podemos resolver varios ejemplos de teoremas de factores. Cada uno de los siguientes ejemplos tiene su respectiva solución detallada. Intente resolver los problemas usted mismo antes de mirar la solución para que pueda practicar y dominar completamente este tema.
EJERCICIO 1
Determina si (x+2) es un factor del polinomio $latex f(x) = {x}^2 + 2x – 4$.
Solución
Primero, tenemos que probar si (x+2) es un factor o no:
Podemos comenzar escribiendo de la siguiente manera:
x+2=0, donde x=-2
Ahora, podemos probar si f(c)=0 según el teorema del factor:
$latex f(x) = {x}^2 + 2x – 4$
$latex f(-2) = {-2}^2 +2 (-2)- 4$
$latex f(-2) = – 4$
Dado que f(-2) no es igual a cero, (x+2) no es un factor del polinomio dado.
EJERCICIO 2
Determina si (x+3) es un factor del polinomio $latex f(x) = 2{x}^2 + 8x + 6$.
Solución
Vamos a probar si (x+2) es un factor del polinomio o no. Por lo tanto, escribimos de la siguiente manera:
x+3=0, donde x=-3
Ahora, podemos usar el teorema del factor para probar si f(c)=0:
$latex f(x) = 2{x}^2 + 8x +6$
$latex f(-3) = 2{(-3)}^2 +8(-3)+6 $
$latex f(-2) = (18)-24 + 6 $
$latex f(-2) = 0$
Dado que f(-3) es igual a cero, esto significa que (x+3) es un factor polinomial.
EJERCICIO 3
Determina si (x+2) es un factor del polinomio f o no, dado que $latex f(x) = 4{x}^3 – 2{x }^2+ 6x – 8$.
Solución
Para probar si (x+1) es un factor del polinomio o no, podemos comenzar escribiendo de la siguiente manera:
x+1=0, donde x=3
Ahora, probamos si f(c)=0 según el teorema del factor:
$latex f(x) = 4{x}^3 – 2{x }^2+ 6x + 8$
$latex f(-1) = 4{(-1)}^3 – 2{(-1) }^2+ 6(-1) + 8$
$latex f(-1) = (-4 )- 2- 6 + 8$
$latex f(-1) = 4 $
Como f(-1) no es igual a cero, (x+1) no es un factor polinomial de la función.
EJERCICIO 4
Determina cuál de las siguientes funciones polinómicas tiene el factor (x+3):
$latex f(x) = {x}^2-x -6$, $latex g(x) = {x}^2-4x +4$, $latex h(x) = {x}^2-9$
Solución
Tenemos que probar los siguientes polinomios:
$latex f(x) = {x}^2-x -6$, $latex g(x) = {x}^2-4x +4$, $latex h(x) = {x}^2-9$
Asumimos que x+3 es un factor de los polinomios, donde x =-3
Primero,
$latex f(x) = {x}^2-x -6$
$latex f(-3) = {(-3)}^2-(-3) -6$
$latex f(-3) = 9 + 3 -6 $
$latex f(-3) = 6 $
Segundo,
$latex g(x) = {x}^2-4x +4$
$latex g(-3) = {(-3)}^2-4(-3) +4$
$latex g(-3) = 9+12 +4$
$latex g(-3) = 25$
Tercero,
$latex h(x) = {x}^2-9$
$latex h(-3) = {(-3)}^2-9$
$latex h(-3) = 9 – 9$
$latex h(-3) = 0 $
Como resultado, h(-3)=0 es el único que satisface el teorema del factor.
Entonces, h(x) es una función polinomial que tiene el factor (x+3).
EJERCICIO 5
Encuentra la solución exacta de la función polinomial $latex f(x) = {x}^2+ x -6$.
Solución
Para encontrar la solución de la función, podemos asumir que (x-c) es un factor polinomial, donde x=c.
Para satisfacer el teorema del factor, tenemos f(c) = 0. Por lo tanto,
$latex f(x) = {x}^2+ x -6$.
$latex {x}^2+ x -6 = 0$.
Factorizando,
$latex (x+3)(x-2) = 0$.
De esto se deduce que (x+3) y (x-2) son los factores polinómicos de la función.
Entonces, x+3=0, donde x=-3 y x-2=0, donde x=2
Por tanto, las soluciones de la función son -3 y 2.
EJERCICIO 6
Encuentra los factores de este polinomio, $latex F(x)= {x}^2 -9$.
Solución
Para encontrar los factores del polinomio según el teorema del factor, el resultado de dividir un polinomio f(x) entre (x-c) es f(c)=0.
Por lo tanto, podemos escribir:
$latex F(x)= {x}^2 -9$
$latex {x}^2 -9 = F(x)$
$latex {x}^2 -9 = o$
Factorizando, tenemos:
$latex (x+3)(x-3) = 0$.
Entonces, x+3 y x-3 son los factores del polinomio.
Ejercicios del teorema del factor para resolver
Resuelve los siguientes problemas del teorema del factor y prueba tus conocimientos sobre este tema. Usa el teorema del factor detallado arriba para resolver los ejercicios. Si tienes problemas con estos ejercicios, puedes estudiar los ejemplos resueltos anteriormente.
Véase también
¿Interesado en aprender más sobre el teorema del factor? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
