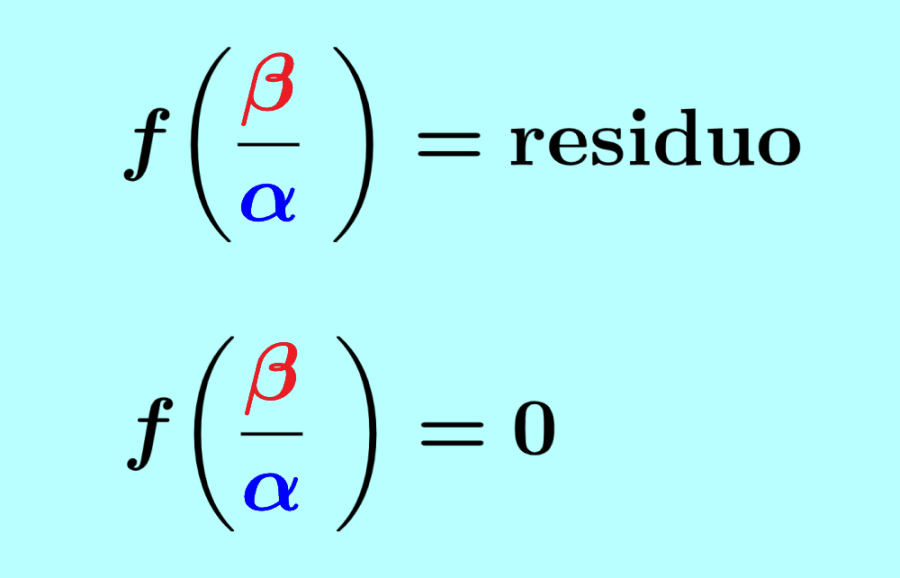Los teoremas del residuo y del factor son dos teoremas algebraicos relacionados con la división y factorización de polinomios. El teorema del residuo nos permite encontrar el residuo cuando dividimos a un polinomio por una expresión lineal. Por otro lado, el teorema del factor nos permite verificar los factores de un polinomio.
A continuación, aprenderemos todo lo relacionado con los teoremas del residuo y del factor. Veremos sus enunciados, las demostraciones de los teoremas y algunos ejemplos.
¿Qué es el teorema del residuo?
El teorema del residuo es un teorema algebraico que indica que cuando dividimos a un polinomio $latex f(x)$ por $latex (\alpha x-\beta)$, el residuo es $latex f\left(\frac{\beta}{\alpha}\right)$.
Esto significa que podemos usar el teorema del residuo para encontrar el residuo de la división de un polinomio por la expresión $latex (\alpha x-\beta)$.
Demostración del teorema del residuo
El resultado de una división es el cociente. Entonces, si es que multiplicamos al cociente por el divisor y sumamos el residuo, obtenemos el polinomio original. Es decir, tenemos:
$$f(x)=(\alpha x-\beta)(\text{Cociente})+(\text{Residuo})$$
Ahora, vamos a usar el valor $latex x=\frac{\beta}{\alpha}$, para obtener lo siguiente:
$$f\left(\frac{\beta}{\alpha}\right)=\left[ \alpha \left(\frac{\beta}{\alpha}\right)-\beta\right](\text{Cociente})+(\text{Residuo})$$
$$=\left[ \beta-\beta\right](\text{Cociente})+(\text{Residuo})$$
$$=\left[ 0 \right](\text{Cociente})+(\text{Residuo})$$
$$=\text{Residuo}$$
Vemos que el teorema del residuo es verdadero, ya que al usar $latex x=\frac{\beta}{\alpha}$ en la función, obtenemos el residuo de la división.
¿Qué es el teorema del factor?
El teorema del factor es un teorema algebraico que nos dice que si es que $latex (\alpha x-\beta)$ es un factor del polinomio $latex f(x)$, entonces, $latex f\left(\frac{\beta}{\alpha}\right)=0$.
Esto significa que el teorema del factor conecta a los factores y a los ceros de un polinomio. El teorema del residuo puede ser considerado como una versión específica de este teorema.
Además, podemos usar el teorema del factor para eliminar los ceros conocidos de un polinomio y dejar intactos todos los ceros desconocidos, lo que da como resultado un polinomio de menor grado con ceros más fáciles de encontrar.
Demostración del teorema del factor
Si es que $latex (\alpha x-\beta)$ es un factor de $latex f(x)$, entonces el residuo es igual a 0 cuando dividimos a $latex f(x)$ por $latex (\alpha x-\beta)$.
Entonces, si es que usamos el teorema del residuo, podemos demostrar que
$$f\left(\frac{\beta}{\alpha}\right)=0$$
Cómo usar el teorema del factor
Los siguientes son los pasos que podemos usar para aplicar el teorema del factor e identificar los factores de un polinomio:
Paso 1: Si es que $latex f(-c)=0$, entonces, $latex (x+ c)$ es un factor del polinomio $latex f(x)$.
Paso 2: Si es que $latex p(\frac{d}{c})= 0$, entonces, $latex (cx-d)$ es un factor del polinomio $latex f(x)$.
Paso 3: Si es que $latex p(-\frac{d}{c})= 0$, entonces, $latex (cx+d)$ es un factor del polinomio $latex f(x)$.
Paso 4: Si es que $latex p(c)=0$ y $latex p(d) =0$, then $latex (x – c)$ and $latex (x -d)$ son factores del polinomio $latex f(x)$.
En lugar de usar el método de división polinomial larga para identificar los factores, el teorema del factor y la división sintética son mejores opciones.
Al usar este teorema, podemos eliminar los ceros conocidos de los polinomios mientras mantenemos intactos todos los ceros desconocidos. Esto nos permite encontrar fácilmente los polinomios de menor grado.
El teorema del factor también se puede definir de otra manera. Por lo general, obtenemos un residuo cuando un polinomio se divide por un binomio. Cuando un polinomio se divide por uno de sus factores binomiales, el cociente obtenido se conoce como polinomio deprimido. El teorema del factor se demuestra de la siguiente manera si el residuo es cero:
El polinomio, digamos $latex f(x)$, tiene un factor $latex (x–c)$ si $latex f(c)=0$, donde $latex f(x)$ es un polinomio de grado $latex n$, donde $latex n$ es mayor o igual a 1 para cualquier número real c.
Ejemplos de los teoremas del residuo y del factor
Los siguientes ejemplos son resueltos aplicando los teoremas del residuo y del factor. Cada ejemplo tiene una solución detallada.
EJEMPLO 1
Encuentra el residuo cuando dividimos al polinomio $latex x^3+5x^2-17x-21$ por $latex x-4$.
Solución: Para resolver esto, tenemos que usar el teorema del residuo.
El teorema del residuo nos dice que cuando $latex f(x)$ es dividido por $latex x-4$, es $latex f(4)$. Entonces, tenemos:
$$f(4)=(4)^3+5(4)^2-17(4)-21$$
$latex =64+80-68-21$
$latex =55$
El residuo de la división es 55.
EJEMPLO 2
Cuando dividimos al polinomio $latex 3x^3+bx^2-7x+5$ por $latex x+3$, el residuo es 17. Encuentra el valor de b.
Solución: En este caso, vamos a usar el teorema del residuo para formar una ecuación y luego resolver para b.
Usando el teorema del residuo, sabemos que $latex f(-3)=17$. Entonces, tenemos:
$$3(-3)^3+b(-3)^2-7(-3)+5=17$$
$latex -81+9b+21+5=17$
$latex 9b=72$
$latex b=8$
El valor de b es 8.
EJEMPLO 3
Determina si es que $latex (x+1)$ es un factor del polinomio $latex f(x) = {x}^2 + x – 2$.
Solución: Para determinar si $latex (x+1)$ es un factor, vamos a usar el teorema del factor.
El teorema del factor nos dice que si es que x+1 es un factor del polinomio, debemos tener $latex f(-1)=0$. Entonces, usando $latex x=-1$ en el polinomio, tenemos:
$latex f(x) = {x}^2 – x -2$
$latex f(-1) = {(-1)}^2 – (-1) -2$
$latex f(-1) = 1 +1 – 2 $
$latex f(-1) = 0$
Vemos que f(-1) = 0. Esto significa que $latex (x + 2)$ es un factor del polinomio dado.
EJEMPLO 4
¿Es $latex (2x-1)$ un factor del polinomio $latex f(x) = 2{x}^2 – x – 1$?
Solución: Nuevamente, vamos a usar el teorema del factor para resolver esto.
Si es que 2x-1 es un factor del polinomio, deberíamos tener $latex f(\frac{1}{2})=0$. Sustituyendo el valor $latex \frac{1}{2}$ en el polinomio, tenemos:
$latex f(\frac{1}{2}) = 2{x}^2 – x – 1$
$latex f(\frac{1}{2}) = 2{(\frac{1}{2})}^2 – (\frac{1}{2}) – 1$
$latex f(\frac{1}{2}) = 2(\frac{1}{4}) – (\frac{1}{2}) – 1$
$latex f(\frac{1}{2}) = \frac{1}{2} – (\frac{1}{2}) – 1$
Obtuvimos $latex f(\frac{1}{2}) = -1$. Esto significa que, (2x–1) no es factor de $latex f(x) = 2{x}^2 – x – 1$.
Véase también
¿Interesado en aprender más sobre los teoremas del residuo y del factor? Puedes mirar estas páginas: