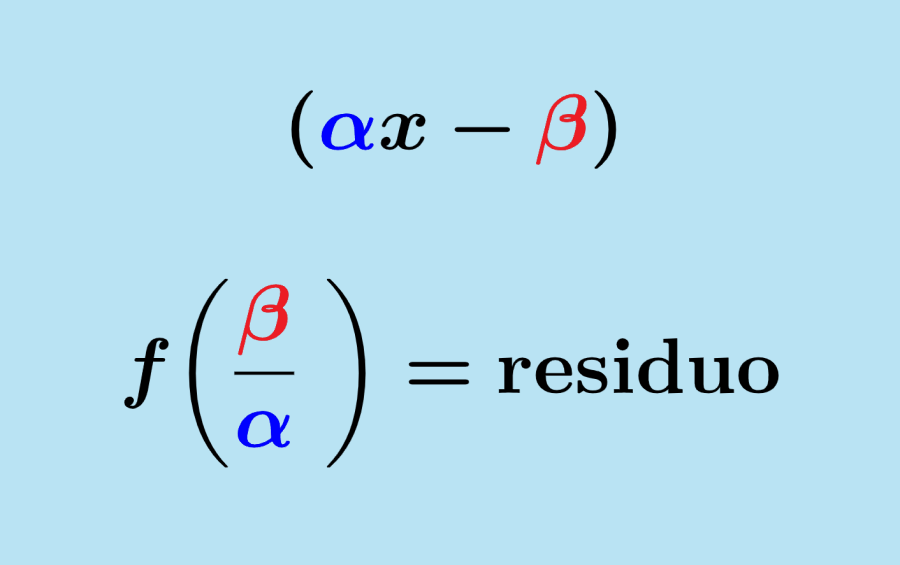El teorema del residuo nos dice que cuando un polinomio f(x) es dividido por (αx-β), el residuo es igual a f(β/α). Esto significa que para encontrar el residuo de la división, tenemos que evaluar a la función usando el valor β/α, es decir, el valor de x del factor (el divisor).
A continuación, veremos 10 ejercicios resueltos del teorema del residuo. Además, podrás poner a prueba tus habilidades con algunos ejercicios de práctica.
10 Ejercicios del teorema del residuo resueltos
Los siguientes ejercicios son resueltos aplicando el teorema del residuo. Cada ejercicio tiene su respectiva solución, pero intenta resolver los ejercicios tú mismo antes de mirar la respuesta.
EJERCICIO 1
¿Cuál es el residuo cuando el polinomio $latex x^3+4x^2+7x+6$ es dividido por $latex x+2$?
Solución
Para encontrar el residuo, podemos usar el teorema del residuo. Este teorema nos dice que el residuo de la división es $latex f\left(\frac{\beta}{\alpha}\right)$.
En este caso, tenemos $latex f\left(\frac{\beta}{\alpha}\right)=f(-2)$. Entonces, tenemos:
$$f(-2)=(-2)^3+4(-2)^2+7(-2)+6$$
$latex =-8+16-14+6$
$latex =0$
Vemos que el residuo es igual a 0. Esto significa que la división es exacta.
EJERCICIO 2
Si es que ahora dividimos al polinomio $latex x^3+4x^2+7x+6$ por $latex x-4$, ¿cuál es el residuo?
Solución
Usando el teorema del residuo sabemos que, el residuo cuando $latex f(x)$ es dividido por $latex x-4$ es $latex f(4)$. Entonces, tenemos:
$$f(4)=(4)^3+4(4)^2+7(4)+6$$
$latex =64+64+28+6$
$latex =162$
El residuo de la división es 162.
EJERCICIO 3
Encuentra el residuo cuando $latex x^3+4x^2-5x+10$ es dividido por $latex x+5$.
Solución
Para resolver esto, podemos usar el teorema del residuo, el cual nos dice que cuando $latex f(x)$ es dividido por $latex x+5$ es $latex f(5)$. Entonces, tenemos:
$$f(-5)=(-5)^3+4(-5)^2-5(-5)+10$$
$latex =-125+100+25+10$
$latex =10$
El residuo de la división es 10.
EJERCICIO 4
Encuentra el residuo cuando $latex x^3-5x^2+4x+2$ es dividido por $latex (2x+1)$
Solución
El teorema del residuo nos dice que el residuo cuando $latex f(x)$ es dividido por $latex 2x+1$ es $latex f\left(-\frac{1}{2}\right)$. Entonces, tenemos:
$$f\left(-\frac{1}{2}\right)=\left(-\frac{1}{2}\right)^3-5\left(-\frac{1}{2}\right)^2+4\left(-\frac{1}{2}\right)+2$$
$latex =-\frac{1}{8}-\frac{5}{4}-2+2$
$latex =-\frac{11}{8}$
El residuo de la división es $latex -\frac{11}{8}$.
EJERCICIO 5
¿Cuál es el residuo cuando $latex 2x^3-2x^2+3x-10$ es dividido por $latex (2x-3)$?
Solución
Usando el teorema del residuo, sabemos que cuando $latex f(x)$ es dividido por $latex 2x-3$ el residuo es $latex f\left(\frac{3}{2}\right)$. Entonces, tenemos:
$$f\left(\frac{3}{2}\right)=\left(\frac{3}{2}\right)^3-2\left(\frac{3}{2}\right)^2+3\left(\frac{3}{2}\right)-10$$
$latex =\frac{27}{8}-\frac{9}{2}+\frac{9}{2}-10$
$latex =-\frac{73}{8}$
El residuo de la división es $latex -\frac{73}{8}$.
EJERCICIO 6
Determina el residuo cuando el polinomio $latex 5x^3-3x^2+4x-10$ es dividido por x.
Solución
En este caso, tenemos simplemente a x. Al comparar con $latex (\alpha x-\beta)$, vemos que $latex \beta$ es igual a 0. Entonces, usamos $latex f\left(\frac{\beta}{\alpha}\right)=f(0)$ para encontrar el residuo:
$$f(0)=5(0)^3-3(0)^2+4(0)-10$$
$latex =0-0+0-10$
$latex =-10$
El residuo de la división es -10.
EJERCICIO 7
Cuando dividimos al polinomio $latex 3x^3+bx^2-7x+5$ por $latex x+3$, obtenemos un residuo de 17. ¿Cuál es el valor de b?
Solución
Podemos resolver esto usando el teorema del residuo. Usando el teorema del residuo, sabemos que $latex f(-3)=17$. Entonces, formamos una ecuación y resolvemos para b:
$$3(-3)^3+b(-3)^2-7(-3)+5=17$$
$latex -81+9b+21+5=17$
$latex 9b=72$
$latex b=8$
El valor de b es 8.
EJERCICIO 8
El polinomio $latex 2x^3+3x^2-cx-2$ nos da un residuo de 10 cuando es dividido por $latex x-2$. Encuentra el valor de c.
Solución
Usando el teorema del residuo, sabemos que $latex f(2)=10$. Entonces, formamos una ecuación y resolvemos para c:
$$2(2)^3+3(2)^2-c(2)-2=10$$
$latex 16+12-2c-2=10$
$latex 2c=16$
$latex c=8$
El valor de c es 8.
EJERCICIO 9
El residuo cuando $latex cx^3+2x^2-5x+7$ es dividido por $latex x-2$ es igual al residuo cuando la misma expresión es dividida por $latex x+1$. Encuentra el valor de c.
Solución
Usando el teorema del residuo, sabemos que $latex f(2)=r$, en donde r es el residuo. Además, dado que el residuo es igual cuando dividimos por $latex x+1$, también tenemos $latex f(-1)=r$.
Entonces, podemos formar una ecuación con $latex f(2)=f(-1)$ y luego resolver para c:
$$c(2)^3+2(2)^2-5(2)+7=c(-1)^3+2(-1)^2-5(-1)+7$$
$$8c+8-10+7=-c+2+5+7$$
$latex 9c=9$
$latex c=1$
El valor de c es igual a 1.
EJERCICIO 10
Cuando dividimos al polinomio $latex f(x)=x^3+ax^2+bx+2$ por $latex x-1$, el residuo es 4 y cuando lo dividimos por $latex x+2$, el residuo también es 4. Encuentra los valores de a y b.
Solución
Usando el teorema del residuo, sabemos que $latex f(1)=4$. Entonces, tenemos:
$$(1)^3+a(1)^2+b(1)+2=4$$
$latex 1+a+b+2=4$
$latex a+b=1$
Ahora, usamos el teorema del residuo con $latex f(-2)=4$ y tenemos:
$$(-2)^3+a(-2)^2+b(-2)+2=4$$
$latex -8+4a-2b+2=4$
$latex 4a-2b=10$
Podemos dividir por 2 a la última ecuación que obtuvimos para simplificarla:
$latex 2a-b=5$
Finalmente, podemos resolver formando un sistema de ecuaciones con las dos ecuaciones encontradas. Al resolver, tenemos $latex a=2$ y $latex b=-1$.
5 Ejercicios de teorema del residuo para resolver
Aplica todo lo aprendido sobre el teorema del residuo para resolver los siguientes ejercicios.
Véase también
¿Interesado en aprender más sobre los teoremas del residuo y del factor? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
