El incentro de un triángulo puede ser encontrado al trazar las bisectrices de los ángulos del triángulo y encontrar su punto de intersección. Además, también podemos calcular las coordenadas del incentro usando una fórmula con las coordenadas de los vértices y las longitudes de los lados del triángulo.
En este artículo, aprenderemos cómo encontrar el incentro de un triángulo usando un método gráfico y un método algebraico. Luego, resolveremos algunos ejercicios de práctica.
¿Qué es el incentro de un triángulo?
El incentro de un triángulo es el punto de intersección de las tres bisectrices del triángulo. A su vez, las bisectrices son los segmentos que dividen a los ángulos por la mitad como podemos ver en el diagrama:
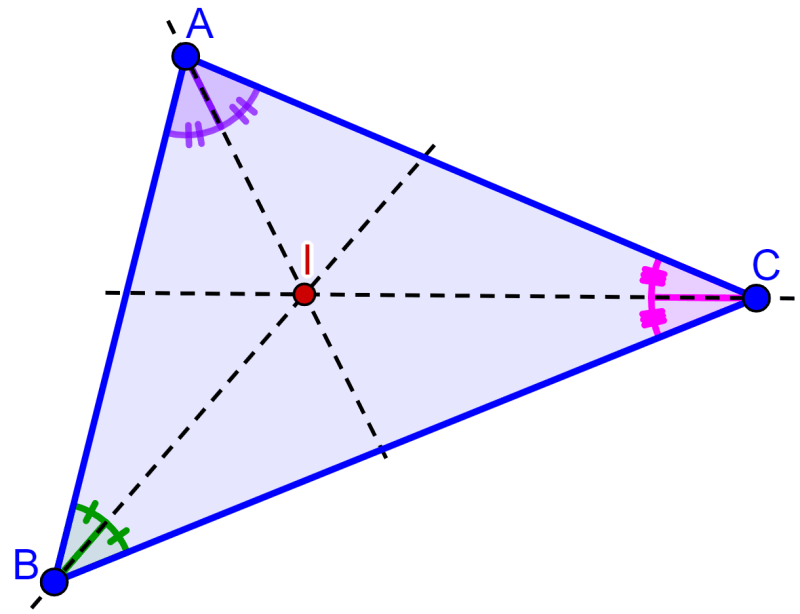
Alternativamente, podemos definir al incentro de un triángulo como el centro de un círculo inscrito en el triángulo. A su vez, un círculo inscrito es el círculo más grande que cabe dentro del triángulo.
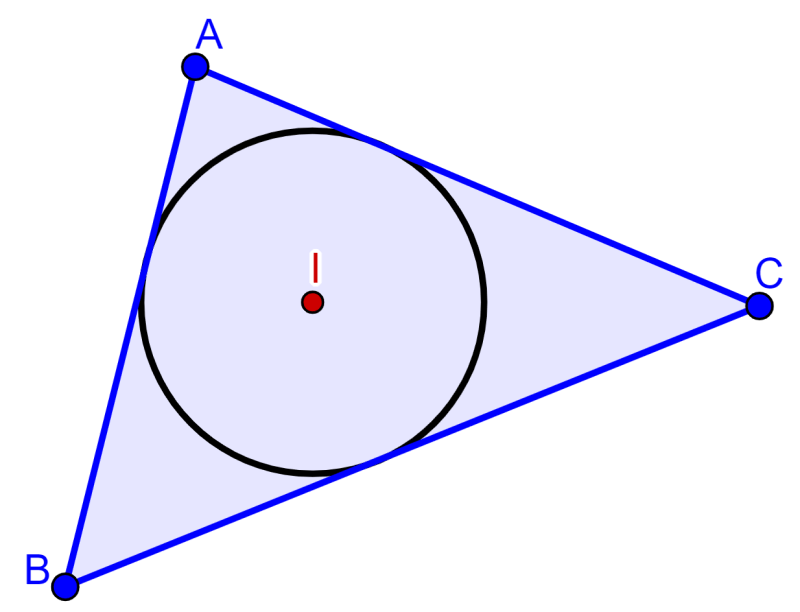
Propiedades del incentro de un triángulo
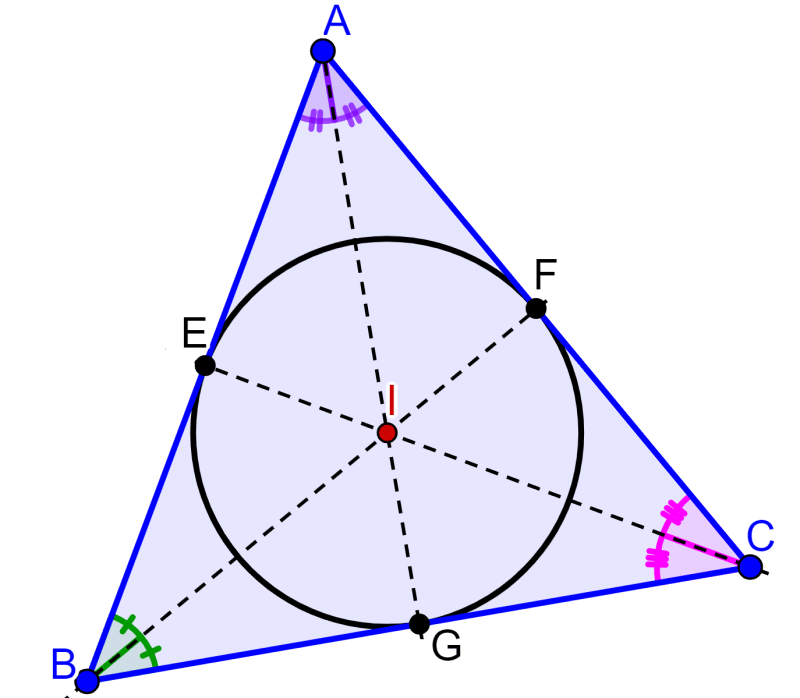
Propiedad 1: El incentro de un triángulo siempre está ubicado dentro del triángulo sin importar el tipo de triángulo que tengamos.
Propiedad 2: Si es que I es el incentro del triángulo, entonces, los segmentos AE, y AF deben tener la misma longitud. Lo mismo sucede con los segmentos BE y BG, y con los segmentos CG y CF.
Propiedad 3: Si es que I es el incentro del triángulo, entonces, los ángulos ∠ABI y ∠CBI son iguales. Lo mismo sucede con los ángulos ∠BAI y ∠CAI, y con los ángulos ∠ACI y ∠BCI.
Propiedad 4: Los lados del triángulo son tangentes al círculo inscrito, por lo que IE, IF e IG son iguales al radio del círculo y son llamados los inradios.
Propiedad 5: El área del triángulo puede ser calculada usando la fórmula A=sr, en donde, r es el inradio del triángulo y s es el semiperímetro. A su vez, el semiperímetro es $latex s=\frac{a+b+c}{2}$.
Encontrar el incentro de un triángulo gráficamente
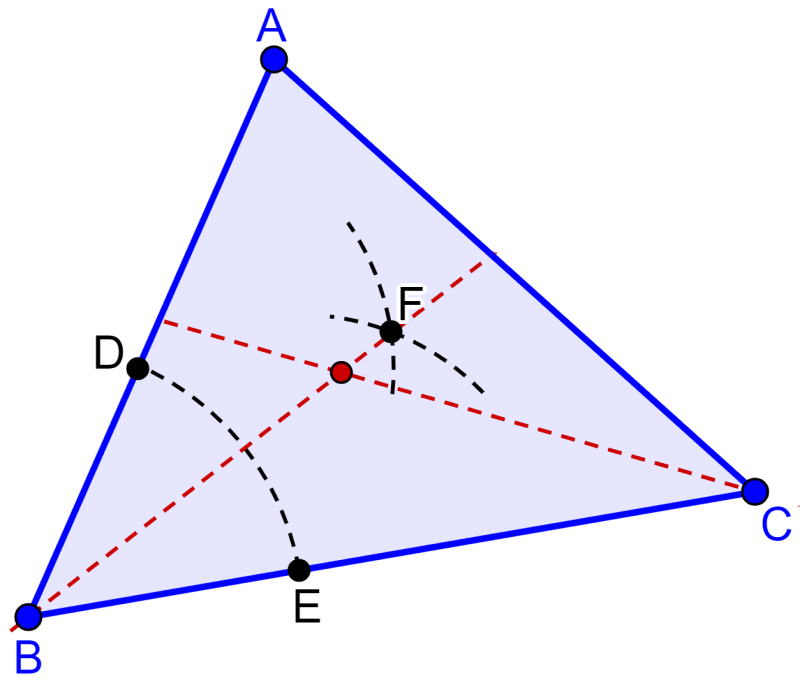
Podemos encontrar al incentro de un triángulo gráficamente al trazar las bisectrices y encontrar el punto de intersección. Entonces, seguimos los siguientes pasos usando un compás:
Paso 1: Centramos al compás en el vértice B y usando cualquier radio, trazamos un arco que corte a ambos lados del triángulo. Entonces, formamos los puntos D y E.
Paso 2: Con el mismo radio, centramos al compás en los puntos D y E para trazar dos arcos y formar el punto de intersección F.
Paso 3: Trazamos un segmento que pase por los puntos B y F. Ese segmento es la bisectriz del ángulo B.
Paso 4: Repitiendo el mismo proceso usando otro vértice del triángulo, podemos trazar otra bisectriz.
Paso 5: Encontramos el punto de intersección de dos bisectrices.
El punto de intersección representa al incentro del triángulo.
Encontrar el incentro de un triángulo algebraicamente
Las coordenadas del incentro del triángulo pueden ser obtenidas algebraicamente usando una fórmula. Sin embargo, necesitamos conocer las coordenadas de los tres vértices y las longitudes de los tres lados.
Supongamos que tenemos al siguiente triángulo:
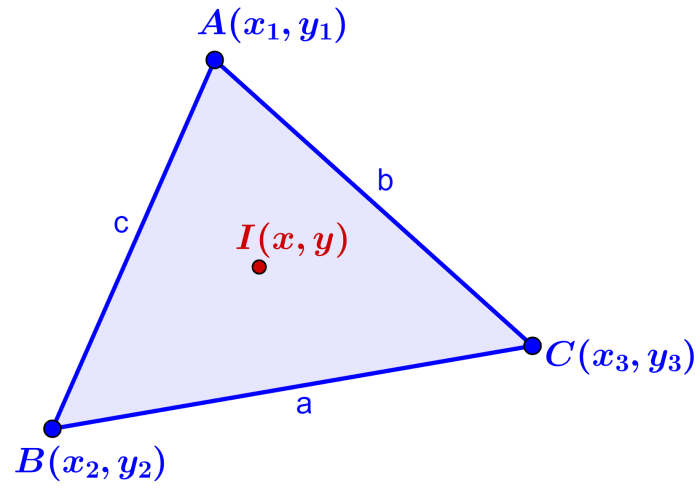
Entonces, podemos calcular el incentro usando la siguiente fórmula:
$$\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c},~\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)$$
en donde, $latex A(x_{1},~y_{1})$, $latex B(x_{2},~y_{2})$ y $latex C(x_{3},~y_{3})$ son las coordenadas de los tres vértices del triángulo y a, b, c son los lados opuestos a cada vértice.
Ejemplos resueltos del incentro de un triángulo
En los siguientes ejemplos, podemos ver cómo encontrar las coordenadas del incentro de un triángulo algebraicamente.
EJEMPLO 1
I representa al incentro del siguiente triángulo. ¿Cuál es la medida del ángulo x?
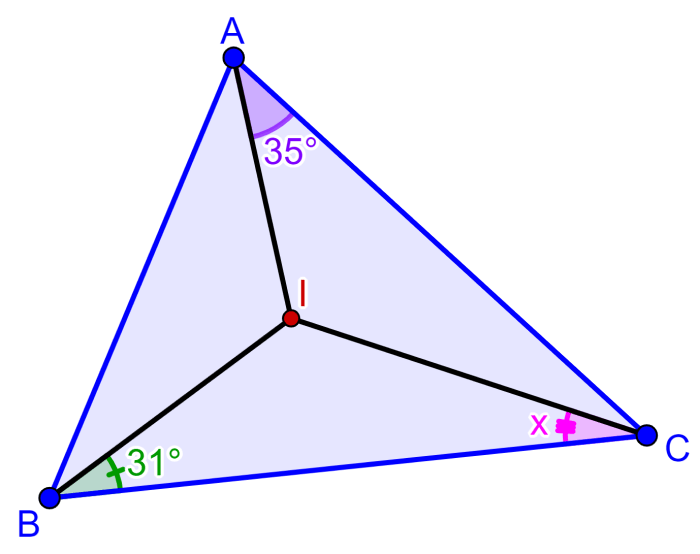
Solución: Dado que I es el incentro del triángulo, los segmentos que conectan al incentro con los vértices son bisectrices, por lo que dividen a los ángulos en dos partes iguales.
Esto significa que los tres ángulos internos del triángulo son:
2×35°=70°
2×31°=62°
2×x=2x
Un triángulo siempre tiene una suma de ángulos internos igual a 180°, por lo que tenemos:
70°+62°+2x=180°
2x=180°-70°-62°
2x=48°
x=24°
EJEMPLO 2
Un triángulo tiene un área de 15 m² y su perímetro es igual a 18 m. ¿Cuál es el radio del círculo inscrito en el triángulo?
Solución: Tenemos lo siguiente:
- Área del triángulo = 15 m²
- Perímetro del triángulo = 18 m
El área de un triángulo puede ser calculada usando A=sr, en donde, s es el semiperímetro y r es el inradio. El semiperímetro es la mitad del perímetro. Entonces, tenemos:
A=sr
15=9r
r=1.67
Entonces, el radio del círculo inscrito es 1.67 m.
EJEMPLO 3
El siguiente triángulo tiene los vértices A(0, 4), B(0, 1) y C(4, 4). ¿Cuáles son las coordenadas de su incentro?
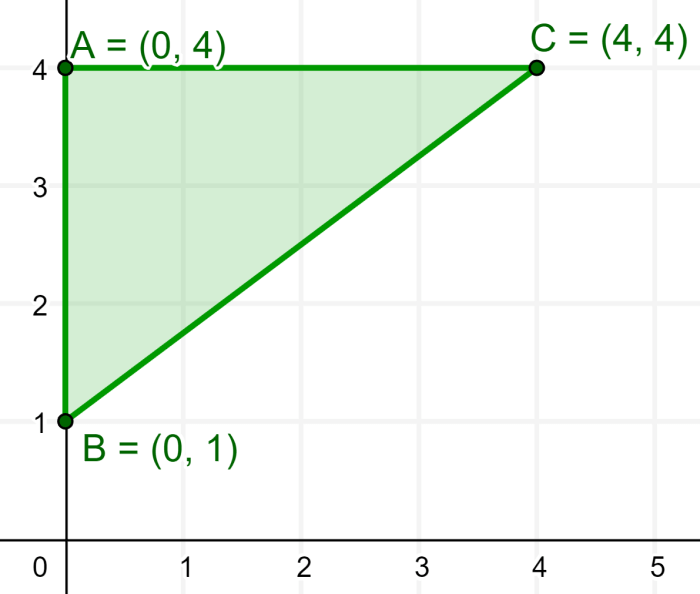
Solución: Podemos usar la fórmula del incentro junto con las coordenadas de los vértices y las longitudes de los lados.
Usando el diagrama, podemos observar que la longitud de b es 4 unidades y la longitud de c es 3 unidades. Entonces, usamos el teorema de Pitágoras con esos dos lados para encontrar la longitud de a:
a²=b²+c²
a²=4²+3²
a²=16+9
a²=25
a=5
Usando la fórmula del incentro, tenemos:
$$\left(\frac{ax_{1}+bx_{2}+cx_{3}}{a+b+c},~\frac{ay_{1}+by_{2}+cy_{3}}{a+b+c}\right)$$
$$=\left(\frac{0+0+3(4)}{5+4+3},~\frac{5(4)+4(1)+3(4)}{5+4+3}\right)$$
$latex =(\frac{12}{12},~\frac{36}{12})$
$latex =(1,~3)$
Las coordenadas del incentro son (1, 3).
Ejercicios para resolver del incentro de un triángulo
Resuelve los siguientes ejercicios usando el método algebraico para encontrar las coordenadas del incentro.
Véase también
¿Interesado en aprender más sobre centroide, incentro, ortocentro y circuncentro de un triángulo? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
