El centroide de un triángulo puede ser encontrado usando un método algebraico o usando un método gráfico. Para encontrar el centroide algebraicamente, tenemos que usar una fórmula y las coordenadas de los vértices del triángulo. Para encontrar el centroide gráficamente, tenemos que trazar dos medianas del triángulo.
En este artículo, aprenderemos cómo encontrar el centroide de un triángulo usando los dos métodos indicados. Luego, resolveremos algunos ejercicios de práctica.
¿Qué es el centroide de un triángulo?
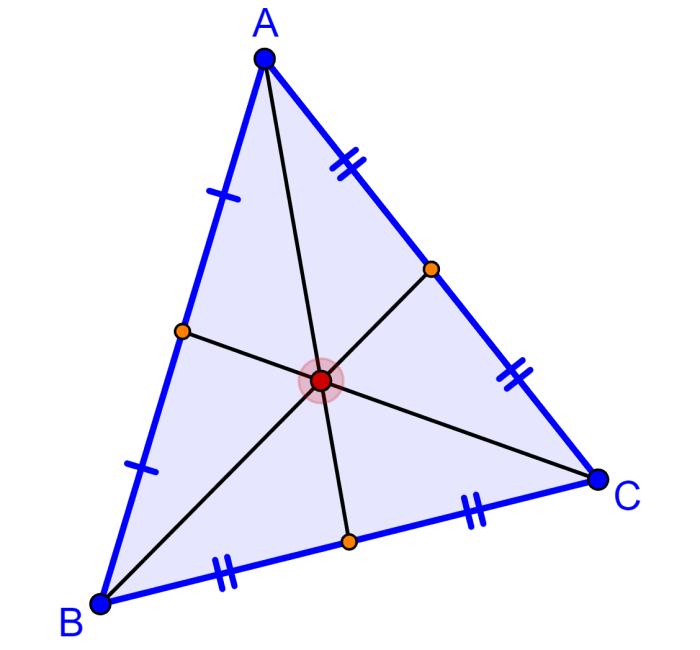
El centroide de un triángulo es el punto de intersección de las tres medianas del triángulo. En el siguiente diagrama, podemos ver que el punto rojo es el centroide:
Recordemos que las medianas del triángulo son los segmentos que conectan a un vértice con el punto medio de su lado opuesto. Esto significa que el centroide es el centro geométrico del triángulo.
Propiedades del centroide de un triángulo
Las siguientes son algunas de las propiedades y características importantes del centroide de un triángulo:
- El centroide de un triángulo es el punto de intersección de las medianas del triángulo.
- El centroide representa al centro geométrico del triángulo.
- El centroide de un triángulo siempre se ubica dentro del triángulo.
- El centroide de un triángulo equilátero se ubica en la misma posición que su incentro, ortocentro y circuncentro.
- El centroide divide a las medianas en una proporción de 2:1.
Encontrar el centroide de un triángulo gráficamente
El centroide de un triángulo puede ser encontrado gráficamente al trazar las medianas del triángulo y determinar su punto de intersección.
A su vez, podemos encontrar las medianas al encontrar el punto medio de cada lado y trazar un segmento desde ese punto hasta el vértice opuesto. Realizamos esto con los siguientes pasos:
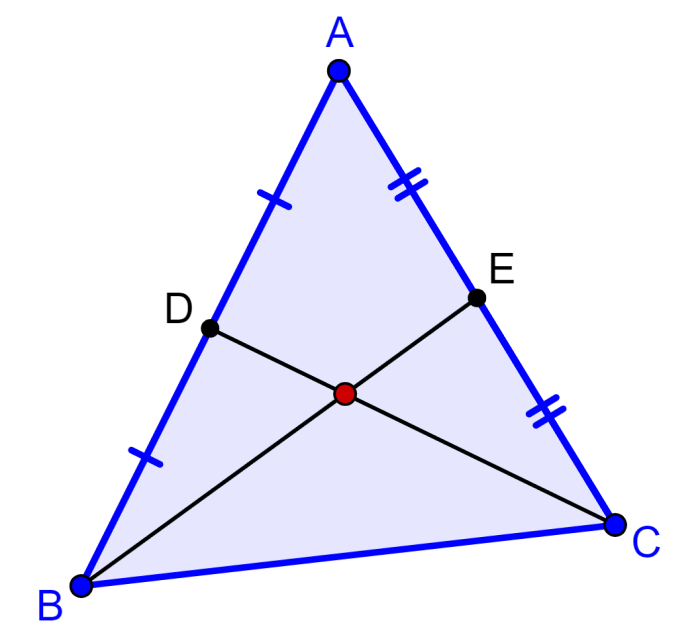
Paso 1: Medimos la longitud del lado AB y marcamos su punto medio para obtener el punto D.
Paso 2: Trazamos un segmento desde el vértice C hasta el punto D.
Paso 3: Medimos la longitud del lado AC y marcamos su punto medio para obtener el punto E.
Paso 4: Trazamos un segmento desde el vértice B hasta el punto E.
Paso 5: Señalamos el punto de intersección de los segmentos AB y AC.
Los segmentos AB y AC son las medianas del triángulo. Esto significa que el punto de intersección es el centroide del triángulo.
Encontrar el centroide de un triángulo algebraicamente
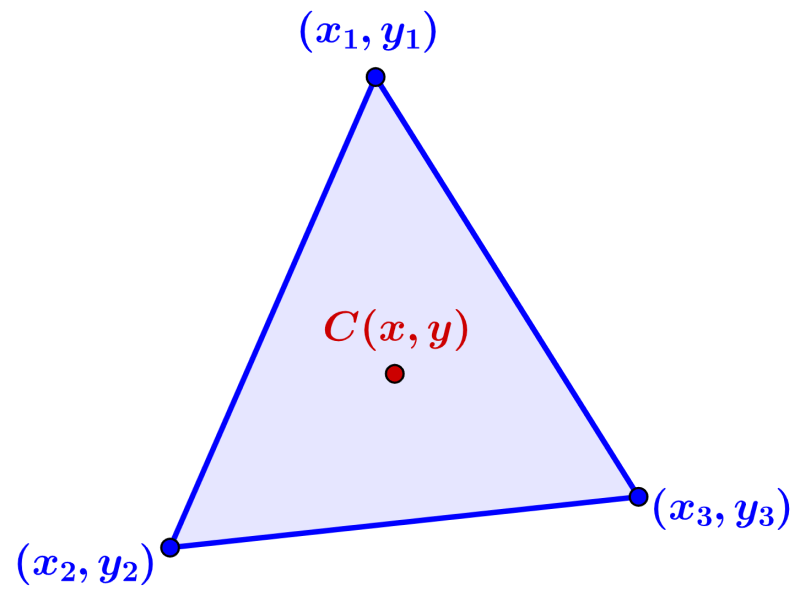
El centroide de un triángulo puede ser encontrado algebraicamente si es que conocemos las coordenadas de los vértices del triángulo. Podemos seguir el proceso usando el siguiente triángulo.
En este triángulo, ($latex x_{1},~y_{1}$), ($latex x_{2},~y_{2}$), ($latex x_{3},~y_{3}$) son los vértices y el punto C(x, y) es el centroide del triángulo.
Entonces, usamos la siguiente fórmula:
$latex C(x, y)=\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)$
Básicamente, tenemos que sumar las coordenadas en x de los vértices y dividir la suma para 3 para obtener la coordenada en x del centroide. De igual forma, sumamos las coordenadas en y de los vértices y dividimos la suma para 3 para obtener la coordenada en y del centroide.
Ejemplos resueltos del centroide de un triángulo
En los siguientes ejemplos, aplicamos el método algebraico para encontrar el centroide de los triángulos.
EJEMPLO 1
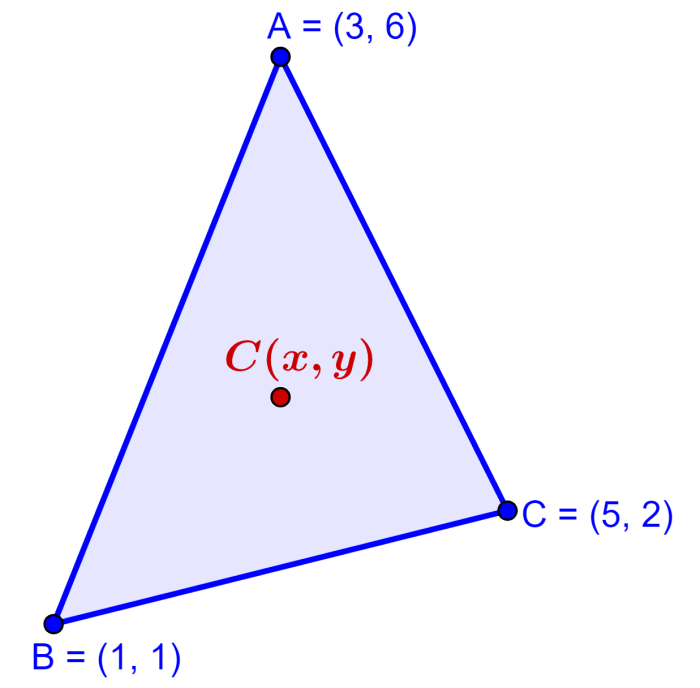
¿Cuáles son las coordenadas del centroide de un triángulo que tiene los vértices A(3, 6), B(1, 1) y C(5, 2)?
Solución: Tenemos que usar la fórmula del centroide con las siguientes coordenadas:
- $latex (x_{1},~y_{1})=(3, ~6)$
- $latex (x_{2},~y_{2})=(1,~1)$
- $latex (x_{3},~y_{3})=(5,~2)$
Entonces, tenemos:
$latex C(x, y)=\left(\frac{x_{1}+x_{2}+x_{3}}{3},~\frac{y_{1}+y_{2}+y_{3}}{3}\right)$
$latex C(x, y)=\left(\frac{3+1+5}{3},~\frac{6+1+2}{3}\right)$
$latex C(x, y)=\left(\frac{9}{3},~\frac{9}{3}\right)$
$latex C(x, y)=(3,~3)$
EJEMPLO 2
¿Cuáles son las coordenadas del centroide de un triángulo que tiene los vértices A(5, 7), B(2, 3) y C(6, 4)?
Solución: Tenemos las siguientes coordenadas:
- $latex (x_{1},~y_{1})=(5, ~7)$
- $latex (x_{2},~y_{2})=(2,~3)$
- $latex (x_{3},~y_{3})=(6,~4)$
Entonces, usando la fórmula del centroide, tenemos:
$latex C(x, y)=\left(\frac{x_{1}+x_{2}+x_{3}}{3},~\frac{y_{1}+y_{2}+y_{3}}{3}\right)$
$latex C(x, y)=\left(\frac{5+2+6}{3},~\frac{7+3+4}{3}\right)$
$latex C(x, y)=\left(\frac{13}{3},~\frac{14}{3}\right)$
Ejercicios para resolver del centroide de un triángulo
Resuelve los siguientes ejercicios usando el método algebraico para encontrar las coordenadas del centroide.
Véase también
¿Interesado en aprender más sobre centroide, incentro, ortocentro y circuncentro de un triángulo? Mira estas páginas: