El teorema de Pitágoras es una de las fórmulas más conocidas en las matemáticas. Este teorema define a la relación entre los lados de un triángulo rectángulo. El teorema de Pitágoras es usado para encontrar las longitudes de algún lado desconocido en un triángulo rectángulo. Además, a través del teorema de Pitágoras, otras fórmulas matemáticas importantes son derivadas, como por ejemplo, las identidades Pitagóricas.
A continuación, veremos un resumen del teorema de Pitágoras junto con algunos ejemplos de práctica.
Resumen del teorema de Pitágoras
El teorema de Pitágoras es una fórmula que relaciona a los lados de un triángulo rectángulo. El teorema de Pitágoras indica que «En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados».
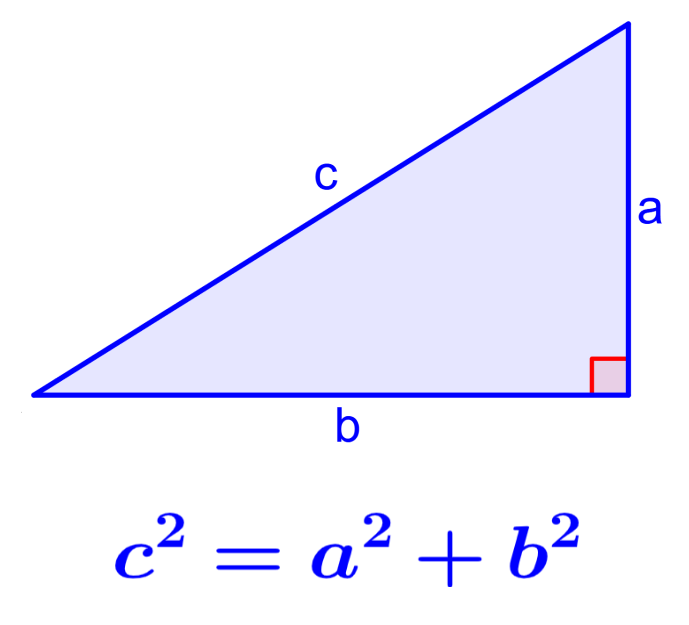
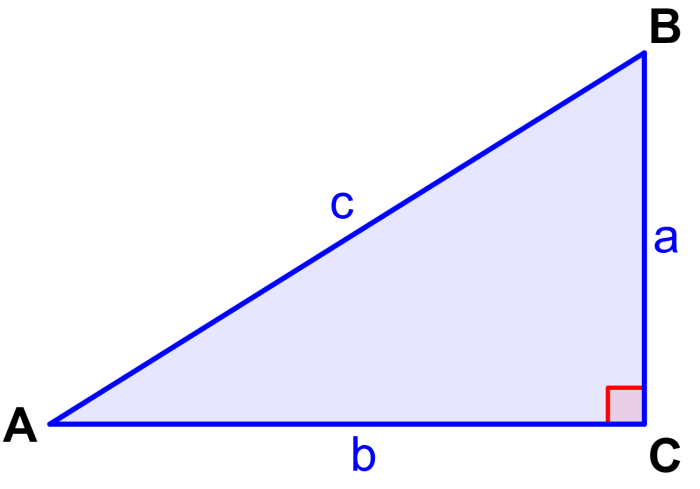
Podemos ilustrar esta idea usando el siguiente triángulo:
En este triángulo, el teorema de Pitágoras es igual a
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
en donde, a, b representan a los catetos del triángulo y c representa a la hipotenusa.
El teorema de Pitágoras puede ser aplicado en las siguientes situaciones:
- Queremos encontrar la longitud de la hipotenusa y tenemos las longitudes de los dos catetos.
- Queremos encontrar la longitud de un cateto y conocemos la longitud de la hipotenusa y la longitud del otro cateto.
Ejemplos de teorema de Pitágoras resueltos
Los siguientes ejemplos muestran cómo aplicar el teorema de Pitágoras para resolver problemas. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJEMPLO 1
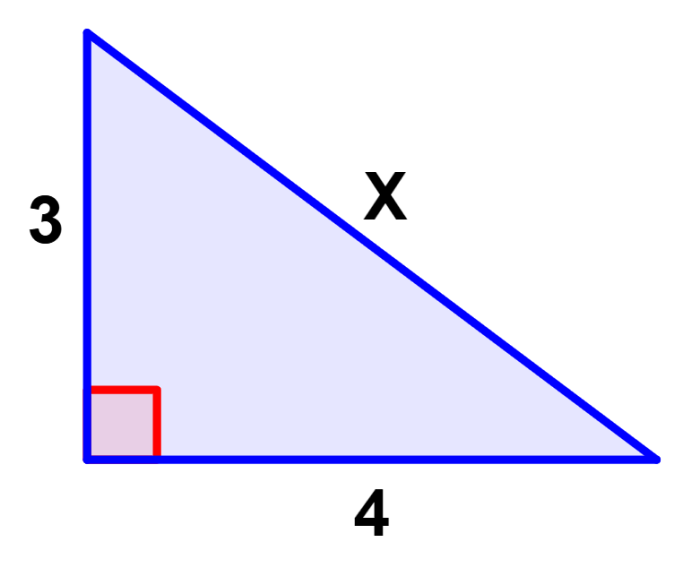
Determina la longitud de X usando el teorema de Pitágoras.
Solución
La longitud que queremos encontrar corresponde a la hipotenusa del triángulo. Entonces, tenemos las dos longitudes de los catetos:
- a=3
- b=4
Aplicamos el teorema de Pitágoras usando las dos longitudes dadas y tenemos:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{3}^2}+{{4}^2}$
$latex {{c}^2}=9+16$
$latex {{c}^2}=25$
$latex c=\sqrt{25}$
$latex c=5$
La longitud de X es 5.
EJEMPLO 2
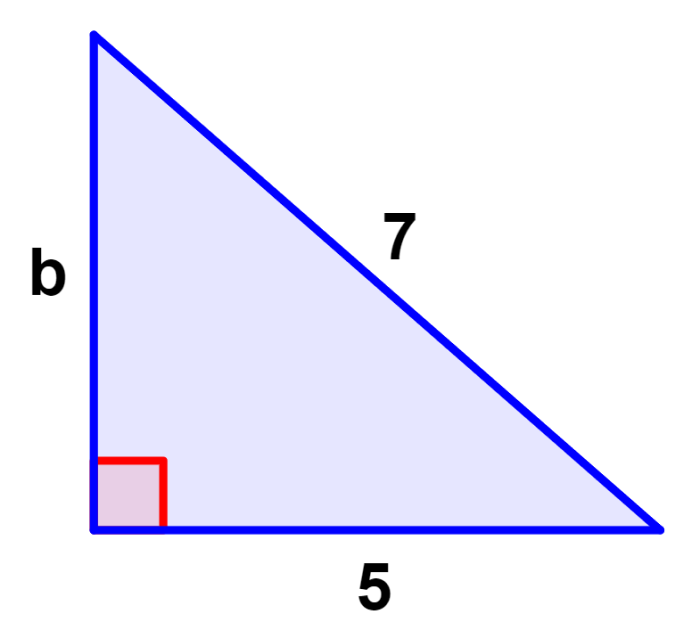
Usa el teorema de Pitágoras para encontrar la longitud faltante.
Solución
Tenemos la longitud de la hipotenusa y uno de los catetos y queremos encontrar la longitud del otro cateto. Entonces, extraemos lo siguiente:
- a=5
- c=7
Usando el teorema de Pitágoras con estos valores, tenemos:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{7}^2}={{5}^2}+{{b}^2}$
$latex 49=25+{{b}^2}$
$latex {{b}^2}=49-25$
$latex {{b}^2}=24$
$latex b=4.9$
La longitud de b es 4.9.
EJEMPLO 3
Un triángulo rectángulo tiene catetos de longitud 9 y 13. ¿Cuál es la longitud de su hipotenusa?
Solución
De la pregunta, tenemos las siguientes longitudes:
- a=9
- b=13
Entonces, vamos a usar estos valores en el teorema de Pitágoras para encontrar la longitud de la hipotenusa:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{9}^2}+{{13}^2}$
$latex {{c}^2}=81+169$
$latex {{c}^2}=250$
$latex c=15.8$
La hipotenusa mide 15.8.
EJEMPLO 4
¿Cuál es la longitud del otro cateto de un triángulo rectángulo que tiene una hipotenusa de 18 y un cateto de 12?
Solución
Tenemos los siguientes datos:
- a=12
- c=18
Entonces, usamos el teorema de Pitágoras junto con estos datos para encontrar el valor de b:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{18}^2}={{12}^2}+{{b}^2}$
$latex 324=144+{{b}^2}$
$latex {{b}^2}=324-144$
$latex {{b}^2}=180$
$latex b=13.4$
La longitud del otro cateto es 13.4.
EJEMPLO 5
Carlos quiere limpiar la ventana de su edificio, la cual está ubicada a 4 m de altura. Él tiene una escalera que mide 4.5 m. ¿A qué distancia desde el edificio debe ubicar a la escalera?
Solución
La longitud de la escalera es fija y al colocarla inclinada en el edificio, formamos un triángulo rectángulo, en donde, la escalera es la hipotenusa, el edificio es la altura y la base es la distancia desde el edificio hasta la escalera.
Entonces, tenemos los siguientes valores:
- a=4
- c=4.5
Tenemos que usar el teorema de Pitágoras para encontrar el valor de b:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{4.5}^2}={{4}^2}+{{b}^2}$
$latex 20.25=16+{{b}^2}$
$latex {{b}^2}=20.25-16$
$latex {{b}^2}=4.25$
$latex b=2.06$
La distancia desde el edificio hasta donde debe ubicarse la escalera es 2.06 m.
Ejemplos de teorema de Pitágoras para resolver
Aplica el teorema de Pitágoras para resolver los siguientes ejemplos. Selecciona una respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre teorema de Pitágoras? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
