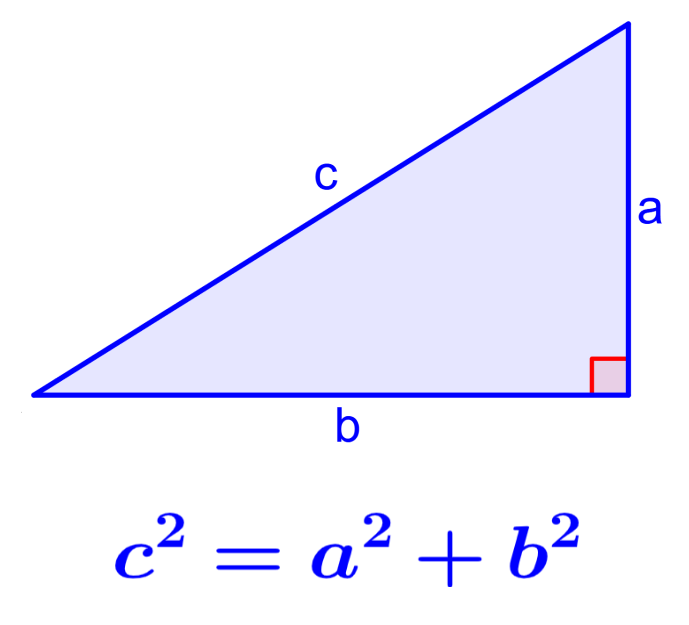
El teorema de Pitágoras es una ecuación o fórmula que nos permite relacionar a los tres lados de un triángulo rectángulo. En geometría, el teorema de Pitágoras es principalmente usado para determinar las longitudes de los lados de un triángulo rectángulo. Adicionalmente, este teorema es usado para derivar otras fórmulas importantes como las identidades Pitagóricas.
A continuación, haremos una revisión breve del teorema de Pitágoras. Conoceremos su fórmula y la aplicaremos para resolver algunos ejercicios.
Revisión del teorema de Pitágoras
El teorema de Pitágoras es una manera de relacionar las longitudes de los tres lados en un triángulo rectángulo. El teorema de Pitágoras dice que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Recordemos que la hipotenusa es el lado del triángulo opuesto al ángulo recto (90°) y los catetos son los otros dos lados del triángulo. Vamos a usar al siguiente triángulo para ilustrar esto:
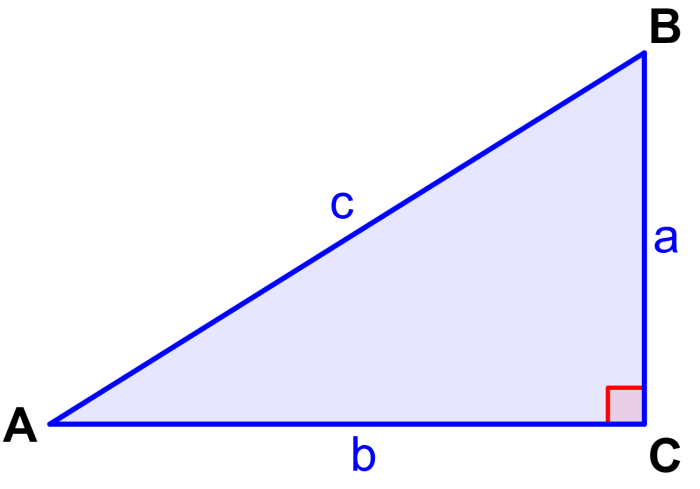
En este triángulo, la fórmula del teorema de Pitágoras es:
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
en donde, a y b son las longitudes de los catetos del triángulo y c es la longitud de la hipotenusa.
Podemos usar el teorema de Pitágoras cuando queremos resolver alguna de las siguientes situaciones:
- Conocemos las longitudes de los dos catetos y queremos encontrar la longitud de la hipotenusa.
- Conocemos la longitud de la hipotenusa y la longitud de un cateto y queremos encontrar la longitud del otro cateto.
Teorema de Pitágoras ejercicios resueltos
El teorema de Pitágoras es usado para encontrar las longitudes de los catetos y la hipotenusa en los siguientes ejercicios. Cada ejercicio tiene su respectiva solución, en donde puedes mirar el proceso usado.
EJEMPLO 1
Encuentra la longitud de X en el siguiente triángulo.
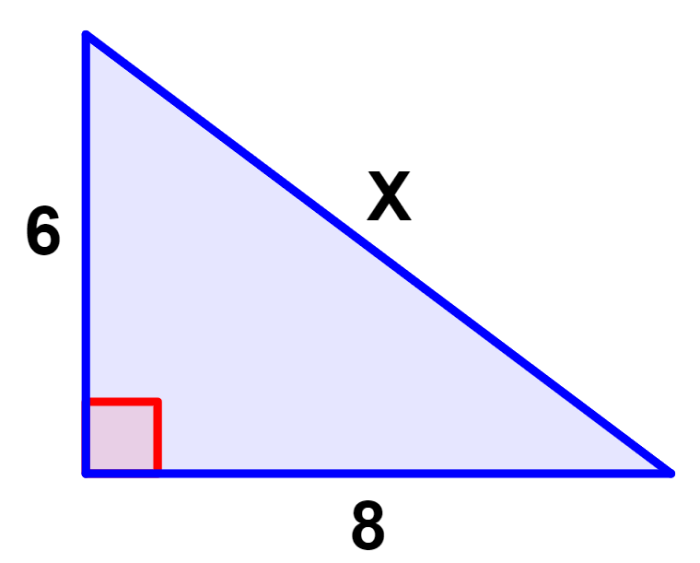
Solución
La longitud de X corresponde a la hipotenusa del triángulo. Además, tenemos las siguientes longitudes:
- a=6
- b=8
Usamos al teorema de Pitágoras con estos valores y tenemos:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{6}^2}+{{8}^2}$
$latex {{c}^2}=36+64$
$latex {{c}^2}=100$
$latex c=\sqrt{100}$
$latex c=10$
La longitud de X es 10.
EJEMPLO 2
¿Cuál es la longitud de Y en el siguiente triángulo?
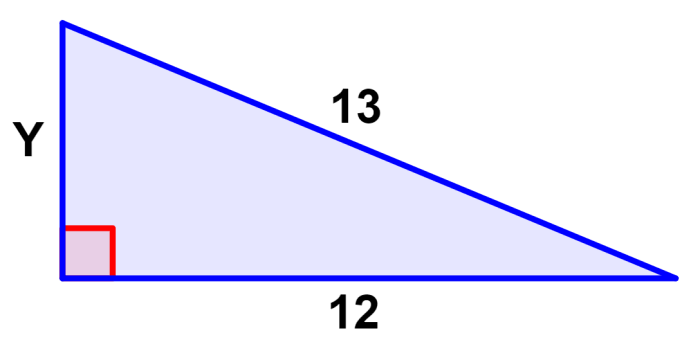
Solución
En este caso, tenemos que encontrar la longitud de uno de los catetos y tenemos las siguientes longitudes:
- a=12
- c=13
Usamos a estas longitudes en el teorema de Pitágoras y tenemos:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{13}^2}={{12}^2}+{{b}^2}$
$latex 169=144+{{b}^2}$
$latex {{b}^2}=169-144$
$latex {{b}^2}=25$
$latex b=5$
La longitud de b es 5.
EJEMPLO 3
¿Cuál es la hipotenusa de un triángulo rectángulo que tiene catetos de longitud 12 y 16?
Solución
Tenemos las longitudes de los catetos:
- a=12
- b=16
Aplicamos el teorema de Pitágoras con estas longitudes para encontrar la longitud de la hipotenusa:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{12}^2}+{{16}^2}$
$latex {{c}^2}=144+256$
$latex {{c}^2}=400$
$latex c=20$
La hipotenusa mide 20.
EJEMPLO 4
Un triángulo rectángulo tiene una hipotenusa de 11 y un cateto de 7? Determina la longitud del otro cateto.
Solución
Tenemos las siguientes longitudes:
- a=7
- c=11
Encontramos la longitud del otro cateto usando el teorema de Pitágoras:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{11}^2}={{7}^2}+{{b}^2}$
$latex 121=49+{{b}^2}$
$latex {{b}^2}=121-49$
$latex {{b}^2}=72$
$latex b=8.5$
La longitud del otro cateto es 8.5.
EJEMPLO 5
Dos ciclistas salen a dar un paseo al mismo tiempo, el uno se va hacia el sur y el otro hacia el oeste. Después de media hora, el ciclista que fue hacia el sur ha viajado 7 kilómetros y el ciclista que fue hacia el oeste ha viajado 8.5 kilómetros.
En ese momento, ¿cuál es la distancia más corta entre ambos?
Solución
Vamos a graficar un diagrama para facilitar la resolución de este problema.
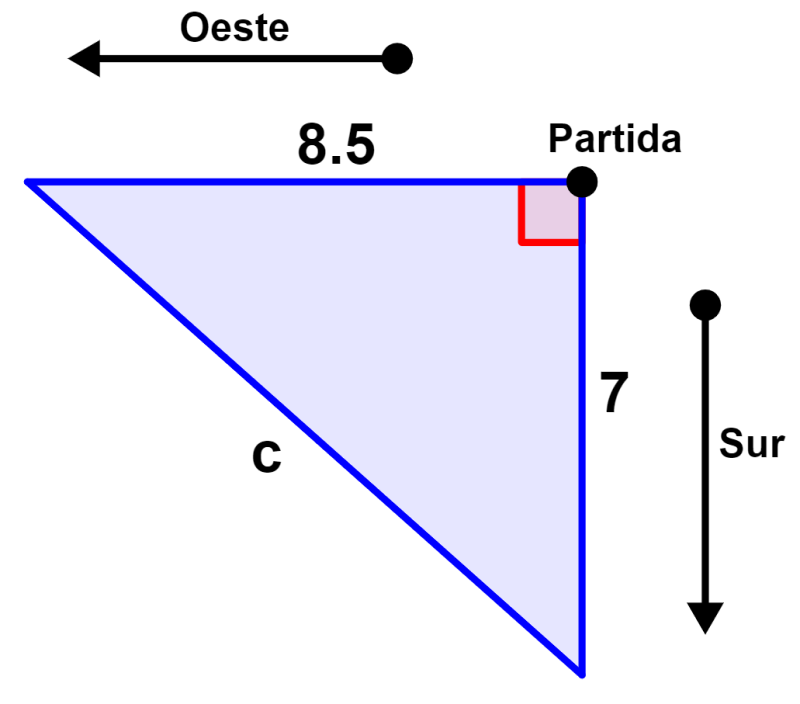
Las direcciones sur y oeste forman un ángulo recto, y la distancia más corta entre dos puntos es una línea recta. Esto significa que la distancia que queremos encontrar es igual a la hipotenusa del triángulo formado. Entonces, usamos el teorema de Pitágoras:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{7}^2}+{{8.5}^2}$
$latex {{c}^2}=49+72.25$
$latex {{c}^2}=121.25$
$latex c=11.01$
La distancia más corta entre ambos es 11.01 kilómetros.
Teorema de Pitágoras ejercicios para resolver
Resuelve los siguientes ejercicios de práctica aplicando el teorema de Pitágoras. Selecciona tu respuesta obtenida y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre el teorema de Pitágoras? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
