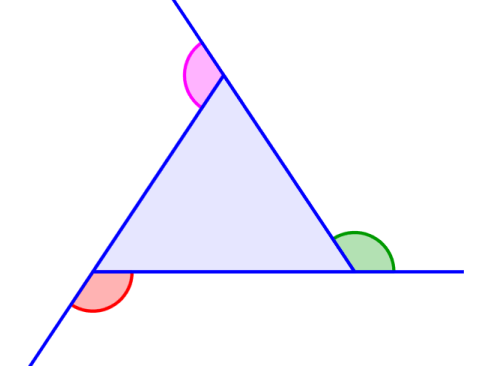
Los ángulos externos de un triángulo son formados cuando extendemos los lados del triángulo. La suma de ángulos externos de un triángulo siempre es igual a 360°. Entonces, dependiendo del tipo de triángulo, podemos aplicar diferentes métodos para encontrar la medida de cada ángulo.
A continuación, aprenderemos cómo determinar la medida de los ángulos externos de diferentes tipos de triángulos. Además, veremos algunos ejemplos de práctica.
Suma de ángulos externos de un triángulo
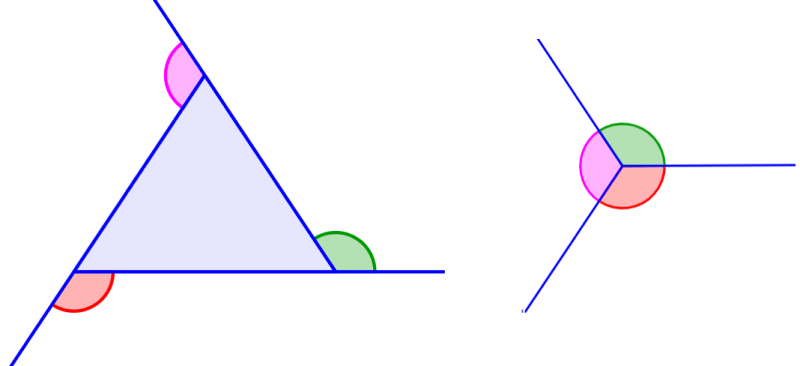
La suma de los ángulos externos de cualquier polígono siempre es igual a 360°. Esto se debe a que, si es que unimos los ángulos externos, formaremos un círculo completo, el cual representa 360°. Podemos ver esto en el siguiente diagrama.
Los ángulos externos son formados al extender los lados del triángulo. Dependiendo del tipo de triángulo, las medidas de cada ángulo externo cambiarán, pero la suma siempre seguirá siendo la misma.
Calcular los ángulos externos de un triángulo equilátero
Un triángulo equilátero es un triángulo que tiene todos sus lados con la misma longitud y todos sus ángulos internos con la misma medida. Esto significa que todos sus ángulos externos también tienen la misma medida.
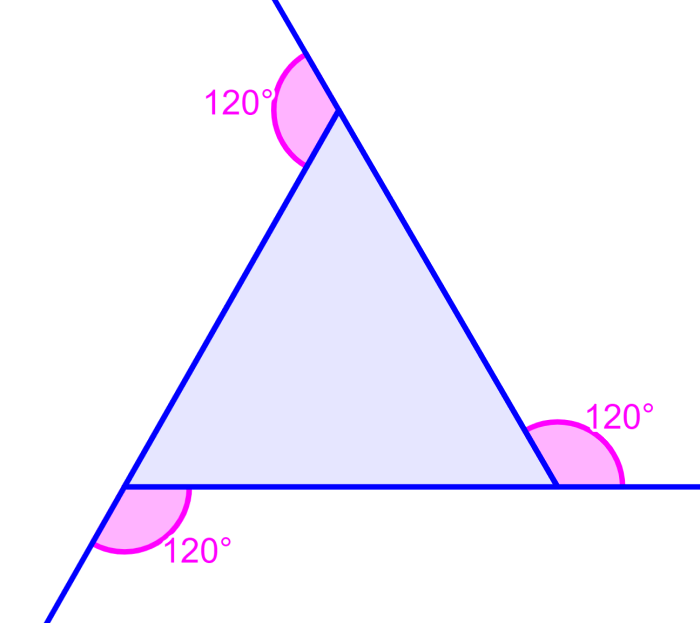
Dado que la suma total de los ángulos externos es igual a 360°, podemos dividir por 3 para obtener la medida de cada ángulo externo en un triángulo equilátero. Entonces, tenemos:
360°÷3=120°
Cada ángulo externo mide 120°.
Calcular los ángulos externos de un triángulo isósceles
Un triángulo isósceles es un triángulo que tiene dos lados con la misma longitud y un tercer lado con longitud diferente. De igual forma, estos triángulos tienen dos ángulos internos con la misma medida y un tercer ángulo con medida diferente. Esto significa que dos ángulos externos tendrán la misma medida y un ángulo externo tendrá una medida diferente.
Para determinar las medidas de los ángulos externos, necesitamos la medida de por lo menos un ángulo externo o interno. Usamos los hechos que la suma de los ángulos externos es igual a 360° y que la suma de un ángulo interno y su ángulo externo correspondiente es igual a 180°.
EJEMPLO 1
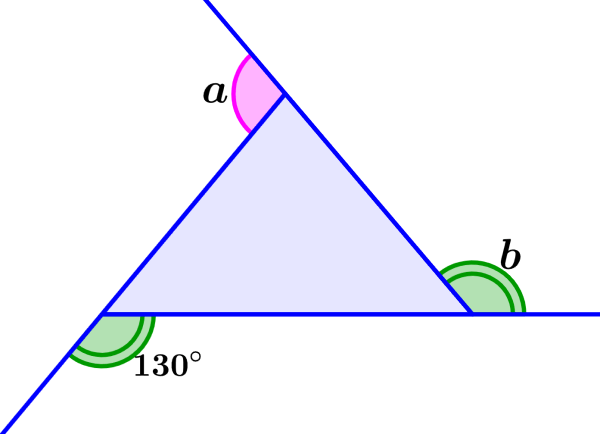
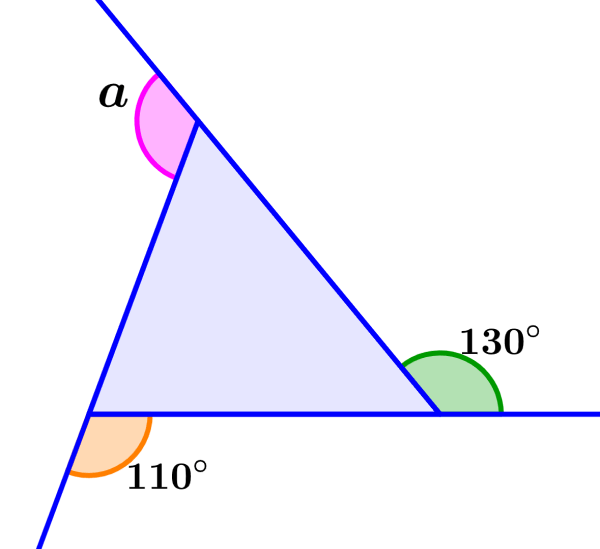
Determina las medidas de los ángulos externos faltantes.
Solution: Los ángulos que están marcados con doble línea son iguales, por lo que tenemos b=130°. Para encontrar la medida del ángulo a, tenemos que sumar las medidas de los ángulos conocidos y restar de 360°. Entonces, tenemos:
130°+130°=260°
⇒ 360°-260°=100°
El ángulo a mide 100°.
EJEMPLO 2
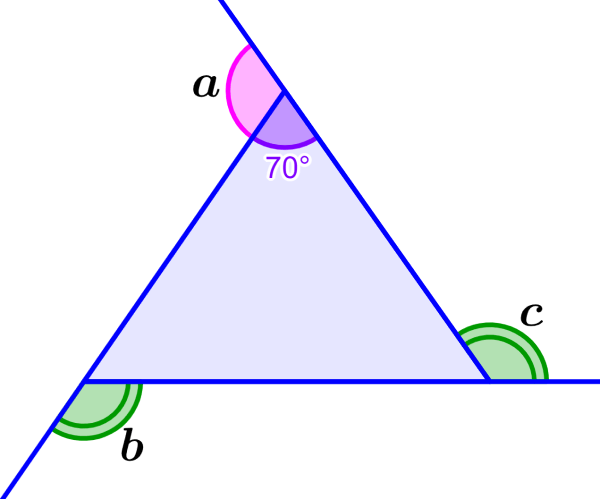
¿Cuáles son las medidas de todos los ángulos externos del triángulo isósceles?
Solucion: En este caso, tenemos la medida de un ángulo interno. Entonces, podemos encontrar la medida de su ángulo externo correspondiente al restar el ángulo de 180°:
180°-70°=110°
La medida del ángulo a es 110°. Ahora, restamos este ángulo de 360° para encontrar las medidas de los otros dos ángulos externos:
360°-110°=250°
Esto corresponde a la suma de ambos ángulos. Dado que ambos ángulos son iguales, dividimos la suma por 2 y tenemos:
250°÷2=125°
Los ángulos b y c miden 125°.
Calcular los ángulos externos de un triángulo escaleno
Los triángulos escalenos tienen todos sus lados con longitudes diferentes y todos sus ángulos internos con medidas diferentes. Esto significa que todos sus ángulos externos también tienen medidas diferentes.
Entonces, para calcular la medida de un ángulo externo, necesitamos conocer la medida de dos ángulos internos o dos ángulos externos.
EJEMPLO 1
Determina la medida del ángulo externo faltante en el siguiente triángulo escaleno.
Solución: Sumamos las medidas de los ángulos conocidos y restamos de 360°. Entonces, tenemos:
110°+130°=240°
⇒ 360°-240°=120°
El ángulo faltante mide 120°.
EJEMPLO 2
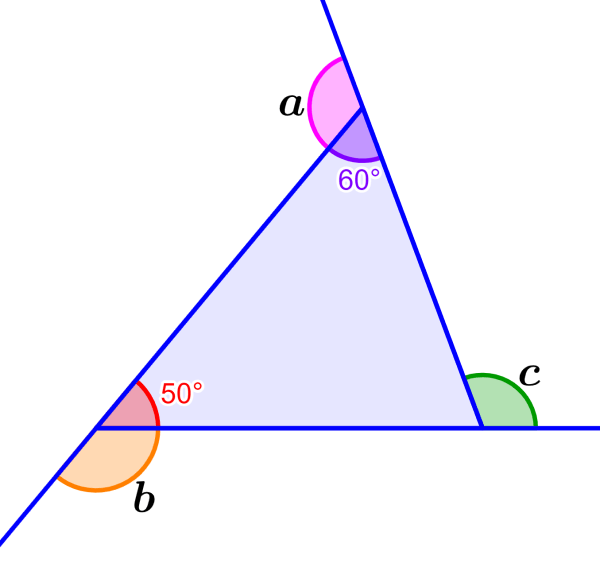
¿Cuáles son las medidas de todos los ángulos externos en el triángulo escaleno?
Solución: En este caso, tenemos dos medidas de los ángulos internos. Podemos calcular las medidas de sus ángulos externos correspondientes al restarlos de 180°:
180°-60°=120°
⇒ a=120°
180°-50°=130°
⇒ b=130°
Ahora, sumamos estos ángulos y los restamos de 360° para obtener la medida del tercero:
120°+130°=250°
⇒ 360°-250°=110°
La medida del ángulo c es 110°.
Véase también
¿Interesado en aprender más sobre ángulos exteriores? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
