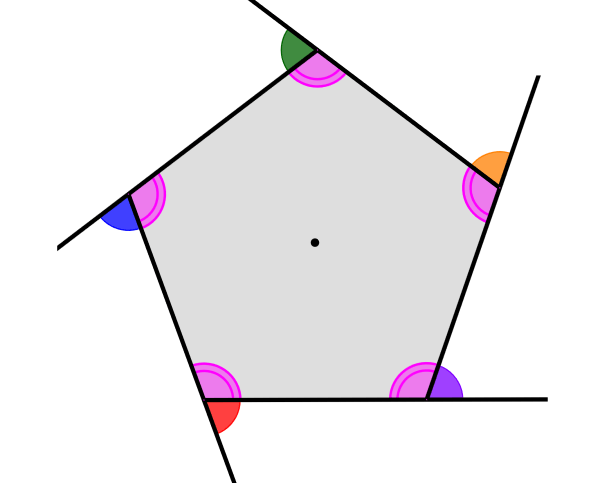
Los ángulos internos de un polígono regular pueden ser calculados usando una fórmula. Esta fórmula nos permite calcular su suma basados en el número de lados del polígono. Por otra parte, la suma de los ángulos externos de cualquier polígono siempre es igual a 360°. Entonces, la medida de cada ángulo es calculada al dividir por el número de lados del polígono regular.
A continuación, conoceremos las fórmulas que podemos usar para determinar los ángulos internos y externos de un polígono.
Calcular la medida de los ángulos internos de un polígono
La medida de cada ángulo interno en un polígono regular puede ser calculada partiendo desde la suma total de los ángulos internos. Por su parte, la suma de los ángulos internos de cualquier polígono es calculada usando la siguiente fórmula:
| $latex (n-2)\times 180$° |
en donde, n es el número de lados del polígono. Por ejemplo, en el caso de un hexágono, usamos $latex n=6$.
Podemos usar esta fórmula para calcular la suma de ángulos internos de cualquier polígono, sin importar si es regular o irregular. Por ejemplo, si es que tenemos un hexágono, el cual tiene seis lados, tenemos:
$latex (n-2)\times 180$°
$latex =(6-2)\times 180$°
$latex =(4)\times 180$°
$latex =720$°
En la siguiente tabla, podemos mirar la suma de ángulos internos de algunos polígonos importantes:
| Polígono | Número de lados | Suma de ángulos |
| Triángulo | 3 | 180° |
| Cuadrilátero | 4 | 360° |
| Pentágono | 5 | 540° |
| Hexágono | 6 | 720° |
| Heptágono | 7 | 900° |
| Octágono | 8 | 1080° |
La medida de cada ángulo interno en un polígono regular es encontrada al dividir la suma total de los ángulos por el número de lados del polígono. Por ejemplo, vimos que la suma de los ángulos internos de un hexágono es igual a 720°. Entonces, cuando dividimos por 6 (lados en un hexágono), tenemos:
720°÷6=120°
Cada ángulo interno de un hexágono regular mide 120°.
Alternativamente, podemos determinar la medida de un ángulo interno en un polígono regular usando la siguiente fórmula:
| $latex \frac{(n-2)\times 180}{n}$ |
en donde, n es el número de lados del polígono regular.
La siguiente es una tabla con los ángulos internos de polígonos importantes:
| Polígono | Cada ángulo |
| Triángulo | 60° |
| Cuadrado | 90° |
| Pentágono | 108° |
| Hexágono | 120° |
| Heptágono | 128.57° |
| Octágono | 135° |
Calcular la medida de los ángulos externos de un polígono
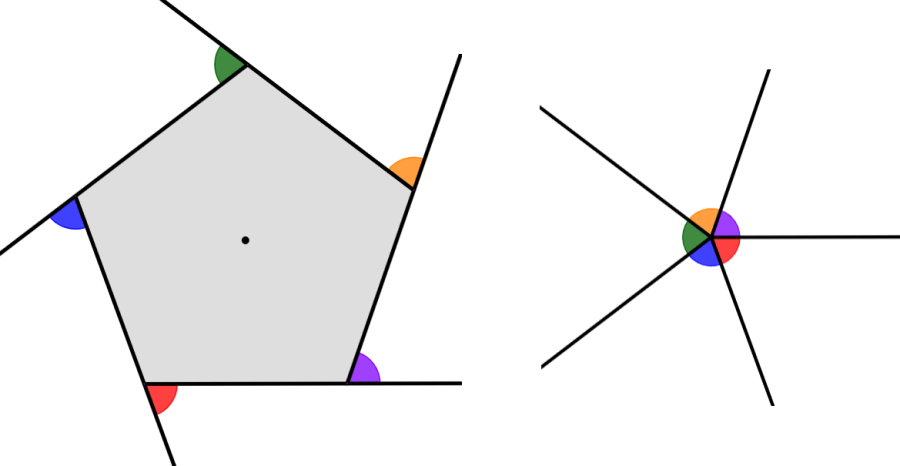
Los ángulos externos de un polígono son formados cuando extendemos a los lados del polígono. Entonces, estos ángulos son formados como en el siguiente diagrama:
Podemos observar que todos los ángulos externos de un polígono tienen una suma total de 360°. Por lo tanto, podemos calcular la medida de uno de los ángulos externos de un polígono regular al dividir 360° por el número de lados del polígono regular. Por ejemplo, para un pentágono, tenemos:
360°÷5=72°
Cada ángulo externo de un pentágono regular mide 72°.
Ejemplos de ángulos internos y externos de un polígono
EJEMPLO 1
¿Cuál es la medida de un ángulo interno de un decágono regular?
Solución: Un decágono es un polígono de 10 lados, por lo que usamos la fórmula de ángulos internos con $latex n=10$. Entonces, tenemos:
$latex \frac{(n-2)\times 180}{n}$
$latex =\frac{(10-2)\times 180}{10}$
$latex =\frac{(8)\times 180}{10}$
$latex =\frac{1440}{10}$
$latex =144$°
La medida de cada ángulo interno de un decágono regular es igual a 144°.
EJEMPLO 2
Encuentra la medida de los ángulos externos de un hexágono regular.
Solución: Un hexágono regular tiene 6 lados, por lo que tenemos que dividir la suma de ángulos externos por 6, ya que todos los ángulos son iguales:
360°÷6=60°
La medida de cada ángulo externo de un hexágono regular es igual a 60°.
Véase también
¿Interesado en aprender más sobre ángulos exteriores? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
