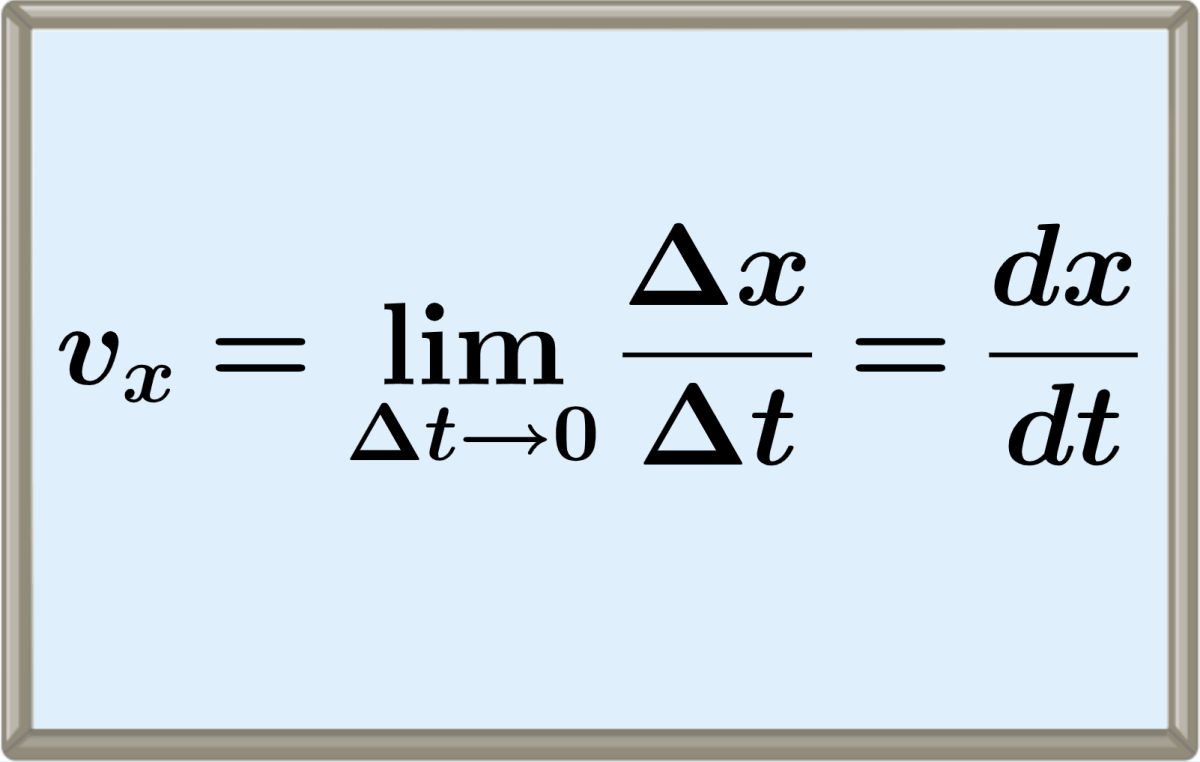En física, la velocidad instantánea describe la velocidad y la dirección de un objeto en un momento determinado. Esta velocidad se puede calcular utilizando el cálculo para hallar la derivada de la posición del objeto con respecto al tiempo.
A continuación, conoceremos la fórmula matemática y los cálculos de la velocidad instantánea. También veremos algunos ejemplos para aprender a calcularla.
¿Qué es la velocidad instantánea en física?
La velocidad instantánea es la velocidad de un objeto en un instante o punto concreto del tiempo. Proporciona una medida más detallada y precisa del movimiento de un objeto en comparación con la velocidad media.
La velocidad instantánea es diferente de la velocidad media, que es el desplazamiento total de un objeto durante un cierto periodo de tiempo, dividido por el intervalo de tiempo. Por otra parte, la velocidad instantánea se refiere a la tasa de cambio de la posición de un objeto en un momento específico – piensa en ella como la velocidad y la dirección de un objeto en un instante exacto.
Una forma útil de visualizar la velocidad instantánea es imaginar que estás conduciendo un auto. El velocímetro indica la velocidad instantánea. Cuando aceleras, desaceleras o cambias de dirección, el velocímetro muestra tu velocidad y dirección en ese preciso momento. En cambio, la velocidad media sería la distancia total recorrida dividida por el tiempo empleado, que no refleja necesariamente la velocidad en un momento dado del trayecto.
Una característica crucial de la velocidad instantánea es que tiene en cuenta la dirección del movimiento, lo que la convierte en una cantidad vectorial. Esto es importante porque significa que la velocidad puede ser positiva o negativa, dependiendo de la dirección del movimiento del objeto.
Comprender la velocidad instantánea es crucial porque desempeña un papel vital en varios aspectos de la física, como la cinemática y la dinámica. También es fundamental para el cálculo, donde se define formalmente como la derivada de la posición con respecto al tiempo. Este conocimiento permite a los físicos predecir las posiciones futuras de un objeto, calcular la aceleración y mucho más.
Fórmula y cálculo de la velocidad instantánea
Matemáticamente, la velocidad instantánea es la tasa de cambio del desplazamiento con respecto al tiempo en un momento determinado. En cálculo, es la derivada de la función de posición con respecto al tiempo o, de forma equivalente, puede definirse como el límite de la velocidad media a medida que el intervalo de tiempo se aproxima a cero.
Esto se puede representar como:
$$v(t)= \lim\limits_{\Delta t\to 0} \frac{ \Delta s}{ \Delta t}$$
$$v(t) = \frac{ds}{dt}$$
en donde
- $latex v(t)$ es la velocidad instantánea
- $latex \frac{ds}{dt}$ es la derivada del desplazamiento ($latex s$) con respecto al tiempo ($latex t$)
- $latex \Delta t$ es el cambio en el tiempo
- $latex \lim\limits_{\Delta t\to 0}$ denota el límite a medida que $latex \Delta t$ se acerca a cero
Esta fórmula proviene del concepto de límite en cálculo. La velocidad media en un intervalo de tiempo $latex \Delta t$ está dada por $latex \frac{\Delta s}{\Delta t}$, donde $latex \Delta s$ es el cambio de posición.
A medida que hacemos este intervalo de tiempo infinitesimalmente pequeño (acercándonos a cero), la velocidad media se convierte en la velocidad instantánea. Por eso la velocidad instantánea se define como la derivada de la posición con respecto al tiempo.
Calcular la velocidad instantánea paso a paso
Ahora, vamos a discutir los pasos para calcular la velocidad instantánea:
- Identificar la función de posición: La función de posición del objeto en movimiento podría ser una función lineal simple, una función cuadrática o cualquier otra función que represente la posición del objeto en diferentes momentos.
- Derivar la función de posición: Esto nos proporcionará la función de velocidad.
- Sustituye el tiempo específico: El resultado será la velocidad instantánea en ese momento concreto del tiempo.
Es importante tener en cuenta que si la velocidad es negativa en un momento determinado, indica que el objeto se estaba moviendo en la dirección opuesta en ese momento. Por el contrario, una velocidad positiva significa movimiento en la dirección positiva.
Velocidad instantánea – Ejemplos con respuestas
Para consolidar la comprensión de la velocidad instantánea, veamos algunos ejemplos con soluciones detalladas.
EJEMPLO 1
Supongamos que un objeto se mueve a lo largo de una línea según la función de posición $latex s(t) = 2t^2 + 3t + 1$, donde $latex s$ está en metros y $latex t$ está en segundos. ¿Cuál es la velocidad instantánea del objeto en $latex t = 2$ segundos?
Solución
En primer lugar, tenemos que derivar la función de posición con respecto al tiempo para obtener la función de velocidad. La derivada de $latex s(t)$ es:
$$v(t) = \frac{ds}{dt}$$
$$v(t) = 4t + 3$$
A continuación, sustituimos $latex t = 2$ en la función de velocidad:
$latex v(2) = 4\times 2 + 3$
$latex v(2) = 11 ~\frac{\text{m}}{\text{s}}$
Por lo tanto, la velocidad instantánea del objeto en $latex t = 2$ segundos es de 11 m/s.
EJEMPLO 2
Considera un auto que se mueve a lo largo de una carretera descrita por la función de posición $latex s(t) = 5t^3 – 7t + 9$, donde $latex s$ está en kilómetros y $latex t$ está en horas. Hallar la velocidad instantánea del auto en $latex t = 1$ horas.
Solución
Derivando la función de posición, obtenemos la función de velocidad:
$$v(t) = \frac{ds}{dt}$$
$latex v(t) = 15t^2 – 7$
Sustituyendo $latex t = 1$ en la función de velocidad:
$latex v(1) = 15\times 1 – 7$
$latex v(1) = 8 ~\frac{\text{km}}{\text{h}}$
Entonces, la velocidad instantánea del auto en $latex t = 1$ horas es de 8 km/h.
EJEMPLO 3
Una partícula se mueve a lo largo de una trayectoria definida por la función de posición $latex s(t) = 3t^2 – 2t + 5$, donde $latex s$ está en metros y $latex t$ está en segundos. Calcular la velocidad instantánea de la partícula en $latex t = 3$ segundos.
Solución
Empezamos por encontrar la derivada de $latex s(t)$:
$$v(t) = \frac{ds}{dt}$$
$latex v(t) = 6t – 2$
Sustituyendo $latex t = 3$ en la función de velocidad:
$latex v(3) = 6\times 3 – 2$
$latex v(3) = 16 ~\frac{\text{m}}{\text{s}}$
Así, la velocidad instantánea de la partícula en $latex t = 3$ segundos es de 16 m/s.
EJEMPLO 4
La posición de un tren se describe mediante la función $latex s(t) = 4t^3 – 3t^2 + 2t – 1$, donde $latex s$ está en kilómetros y $latex t$ está en minutos. ¿Cuál es la velocidad instantánea del tren en $latex t = 2$ minutos?
Solution
La derivada de la función de posición es:
$$v(t) = \frac{ds}{dt}$$
$latex v(t) = 12t^2 – 6t + 2$
Sustituyendo $latex t = 2$ en la función de velocidad:
$latex v(2) = 12\times 4 – 12 + 2 $
$latex v(2)= 34 ~\frac{\text{km}}{\text{min}}$
Por lo tanto, la velocidad instantánea del tren en $latex t = 2$ minutos es de 34 km/min.
Aplicaciones de la velocidad instantánea
La velocidad instantánea puede parecer un concepto reservado principalmente a los libros de física, pero tiene numerosas aplicaciones en nuestra vida cotidiana. Veamos algunas de las más comunes.
Exploración espacial
En la exploración espacial, conocer la velocidad instantánea de una nave espacial es crucial. El cálculo de la velocidad instantánea permite a los ingenieros tomar decisiones en tiempo real sobre ajustes de trayectoria y velocidad. Esto es esencial para ejecutar maniobras complejas.
Análisis del movimiento del vehículo
En la industria del automóvil, el concepto de velocidad instantánea es fundamental en las fases de diseño y ensayo. Por ejemplo, las pruebas de auto necesitan conocer la velocidad exacta en el momento del impacto para analizar la eficacia de las medidas de seguridad.
Otro ejemplo más común es el uso de velocímetros, ya que indican la velocidad instantánea de un auto en un momento determinado.
Deportes y atletismo
En los deportes, especialmente en aquellos en los que intervienen pelotas u otros objetos que se mueven con rapidez, conocer la velocidad instantánea puede ser crucial. Por ejemplo, en el béisbol, la velocidad de un lanzamiento o de una pelota bateada en un momento dado puede afectar significativamente al resultado del partido.
Los sistemas avanzados de seguimiento proporcionan estos datos, mejorando tanto la estrategia como la experiencia del espectador.
Velocidad instantánea en física teórica
Más allá de sus aplicaciones prácticas, la velocidad instantánea es también un concepto fundamental de la física teórica. Desempeña un papel crucial en el estudio del movimiento y la dinámica, la cinemática y la mecánica cuántica.
Veáse también
¿Quiere saber más sobre el movimiento? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
