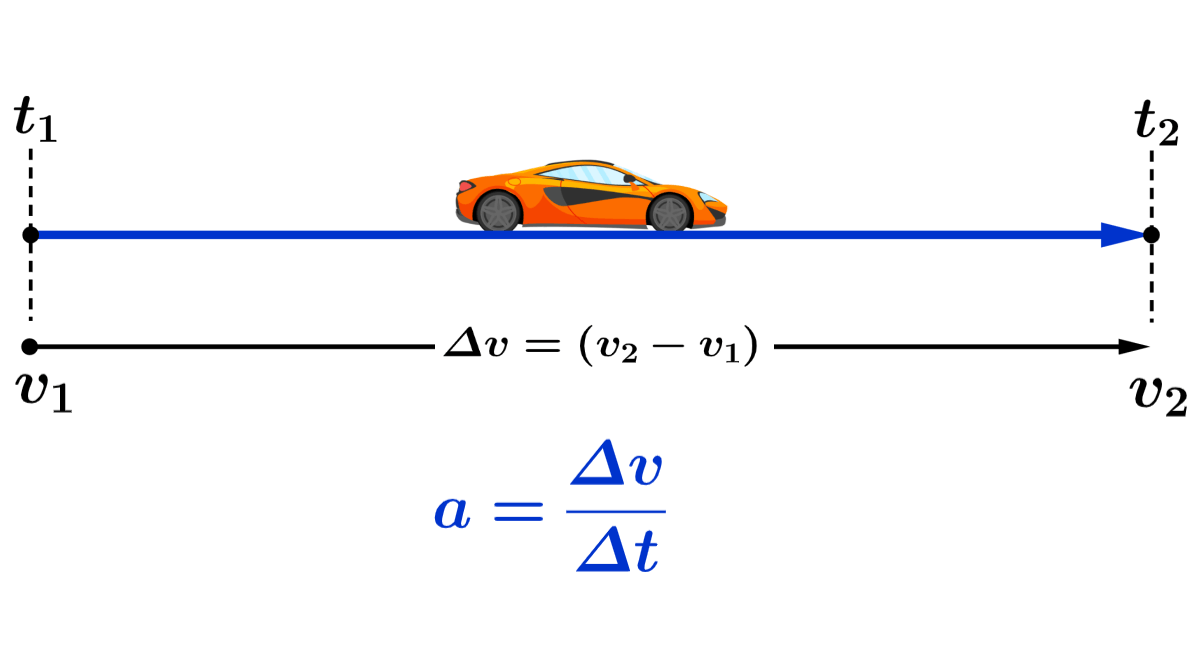En física, entender el movimiento es fundamental, por lo que es necesario entender el concepto de aceleración. La aceleración media es el ritmo al que un objeto cambia su velocidad en un periodo de tiempo determinado. Es una magnitud vectorial, lo que significa que tiene magnitud y dirección.
En este artículo exploraremos en detalle el concepto de aceleración media. Veremos su fórmula, ejemplos y conceptos erróneos comunes.
¿Qué es la aceleración media en física?
En física, la aceleración media se define como el cambio total de velocidad en un periodo de tiempo determinado. Es una medida de la rapidez con la que un objeto cambia su velocidad.
La aceleración es una magnitud vectorial, lo que significa que tiene magnitud y dirección. Por lo tanto, la aceleración media también es una magnitud vectorial.
La aceleración media se mide en unidades de distancia sobre tiempo al cuadrado, como metros por segundo al cuadrado ($latex \frac{\text{m}}{\text{s}^2}$), millas por hora al cuadrado ($latex \frac{\text{mi}}{\text{h}^2}$) o kilómetros por hora al cuadrado ($latex \frac{\text{km}}{\text{h}^2}$).
Matemáticamente, la aceleración media ($latex a_m$) se calcula dividiendo el cambio de velocidad ($latex \Delta v$) por el cambio de tiempo ($latex \Delta t$).
Aceleración media típica de objetos comunes
| Objeto | Aceleración media (m/s²) |
|---|---|
| Caída libre | 9.8 (gravedad) |
| Auto acelerando desde reposo | 1 a 3 |
| Space Shuttle durante el lanzamiento | 29.4 |
| Tren acelerando desde el reposo | 1.1 |
| Ascensor comenzando a ascender | 1 a 2 |
| Un velocista empezando 100 metros lisos | 8 a 10 |
| Avión comercial durante el despegue | 3 |
Estas magnitudes son aproximaciones y pueden variar significativamente en distintas situaciones. Las unidades están en metros por segundo al cuadrado (m/s²), que es la unidad estándar de aceleración.
Fórmula y cálculo de la aceleración media
La aceleración media es una medida del ritmo al que un objeto cambia su velocidad, que puede calcularse mediante la siguiente fórmula:
$$a_{m} = \frac{\Delta v}{\Delta t}$$
donde:
- $latex \Delta v$ representa el cambio en la velocidad, y
- $latex \Delta t$ representa el período de tiempo en el que se produce este cambio.
Recordemos que la aceleración es una magnitud vectorial, lo que significa que tiene magnitud y dirección. Generalmente, especificamos la aceleración media en un eje dado, como el eje $latex x$ o $latex y$.
Si la velocidad se expresa en metros por segundo y el tiempo se expresa en segundos, entonces la aceleración media es en metros por segundo al cuadrado ($latex \frac{\text{m}}{\text{s}^2}$).
Cálculo paso a paso
Veamos ahora paso a paso cómo calcular la aceleración media.
Paso 1: Identificar las velocidades inicial y final, $latex v_{i}$ y $latex v_{f}$, respectivamente.
Paso 2: Calcular $latex \Delta v=v_{f}-v_{i}$.
Paso 3: Identifique el tiempo durante el cual se ha producido el cambio de velocidad. Esto es igual a $latex \Delta t$.
Paso 4: Dividir a $latex \Delta v$ por $latex \Delta t$ para obtener aceleración promedio.
Recuerda que se trata de la aceleración media. Supone que la aceleración del auto ha sido constante durante este periodo de tiempo, lo que no siempre es el caso en el mundo real.
Aceleración media – Ejemplos con respuestas
EJEMPLO 1
Un auto parte del reposo y alcanza una velocidad de 60 m/s en 10 segundos. ¿Cuál es su aceleración media?
Solución
La fórmula de la aceleración media es
$$a_{m}=\frac{v_f-v_i}{\Delta t}$$
donde:
- $latex a_{m}$ es la aceleración media
- $latex v_f$ es la velocidad final
- $latex v_i$ es la velocidad inicial
- $latex \Delta t$ es el cambio en el tiempo
Aquí tenemos, $latex v_i = 0$ m/s (el auto empieza de reposo), $latex v_f = 60$ m/s, y $latex \Delta t = 10$ s. Usando estos valores en la fórmula:
$$a_{m}=\frac{60-0}{10}$$
$latex a_{m}=6~\frac{\text{m}}{\text{s}^2}$
Por lo tanto, la aceleración media del auto es de 6 m/s².
EJEMPLO 2
Un tren reduce su velocidad de 40 m/s a 20 m/s en 5 segundos. ¿Cuál es su aceleración media?
Solución
Utilizando la misma fórmula:
$$a_{m} = \frac{v_f – v_i}{\Delta t}$$
En este caso, $latex v_i = 40$ m/s, $latex v_f = 20$ m/s, y $latex \Delta t = 5$ s. Al usar la fórmula con estos valores se obtiene:
$$a_{m}=\frac{20-40}{5}$$
$latex a_{m}=-4~\frac{\text{m}}{\text{s}^2}$
El signo negativo indica que el tren está desacelerando. Entonces, la aceleración (o deceleración, en este caso) media del tren es de -4 m/s².
EJEMPLO 3
Una bicicleta se desplaza a una velocidad de 12 m/s y se detiene en un período de 4 segundos. ¿Cuál es la aceleración media?
Solución
Volvemos a utilizar la misma fórmula:
$$a_{m} = \frac{Δv }{Δt}$$
En este caso:
- $latex \Delta v =$ velocidad final – velocidad inicial = 0 m/s – 12 m/s = -12 m/s
- $latex \Delta t =$ tiempo final – tiempo inicial = 4 s – 0 s = 4 s
Sustituyendo estos valores:
$$a_{m} = \frac{-12}{ 4} = -3~\text{m/s}^2$$
En este caso, la aceleración es negativa, lo que indica una deceleración (la bicicleta está frenando). La deceleración media de la bicicleta es de 3 m/s².
EJEMPLO 4
Un cohete despega y alcanza una velocidad de 1000 m/s en 50 segundos. ¿Cuál es su aceleración media?
Solución
Utilizamos la siguiente fórmula:
$$a_{m} = \frac{v_f – v_i}{\Delta t}$$
Aquí tenemos, $latex v_i = 0$ m/s (suponiendo que el cohete parte del reposo), $latex v_f = 1000$ m/s, y $latex \Delta t = 50$ s:
$$a_{m}=\frac{1000-0}{50}$$
$latex a_{m}=20~\frac{\text{m}}{\text{s}^2}$
Por lo tanto, la aceleración media del cohete es de 20 m/s².
Conceptos erróneos sobre la aceleración media
Comprender los siguientes conceptos erróneos puede ayudar a profundizar en el conocimiento de la aceleración media y evitar errores al aplicar este concepto en problemas de física.
Concepto erróneo 1: La aceleración media es siempre en la dirección del movimiento
La dirección de la aceleración media está determinada por el cambio de velocidad, no sólo por la dirección del movimiento. Si un objeto se ralentiza (desacelera), la aceleración se produce en la dirección opuesta al movimiento. Por lo tanto, es perfectamente posible que un objeto se mueva en una dirección mientras su aceleración es en la dirección opuesta.
Concepto erróneo 2: Aceleración cero significa que el objeto está en reposo
En realidad, aceleración cero significa que la velocidad del objeto no cambia con el tiempo, no que el objeto esté en reposo. Un objeto en movimiento puede continuar moviéndose a una velocidad y dirección constantes (lo que significa que tiene aceleración cero) sin estar en reposo.
Concepto erróneo 3: La aceleración media y la aceleración instantánea son iguales.
La aceleración media se calcula a lo largo de un intervalo de tiempo y puede dar una idea general de cómo cambia la velocidad a lo largo de ese periodo. Por otro lado, la aceleración instantánea es la aceleración en un momento específico del tiempo y podría ser diferente de la aceleración media si la aceleración no es constante.
Concepto erróneo 4: Una aceleración negativa siempre significa ir más despacio
Si bien es cierto que una aceleración negativa puede representar una desaceleración, también es cierto que puede representar una aceleración hacia la izquierda o hacia abajo (en un sistema de coordenadas estándar), dependiendo del contexto. El signo de la aceleración se refiere a la dirección, no sólo a la aceleración o desaceleración.
Concepto erróneo 5: La aceleración media es siempre constante.
La aceleración media es la tasa media de cambio de la velocidad con respecto al tiempo durante un intervalo específico. No significa que la aceleración haya sido constante durante ese intervalo de tiempo. Una aceleración constante significaría que la velocidad del objeto está cambiando a un ritmo constante, pero esto es un caso específico y no siempre es la situación en escenarios del mundo real.
Veáse también
¿Quieres saber más sobre velocidad y aceleración? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
