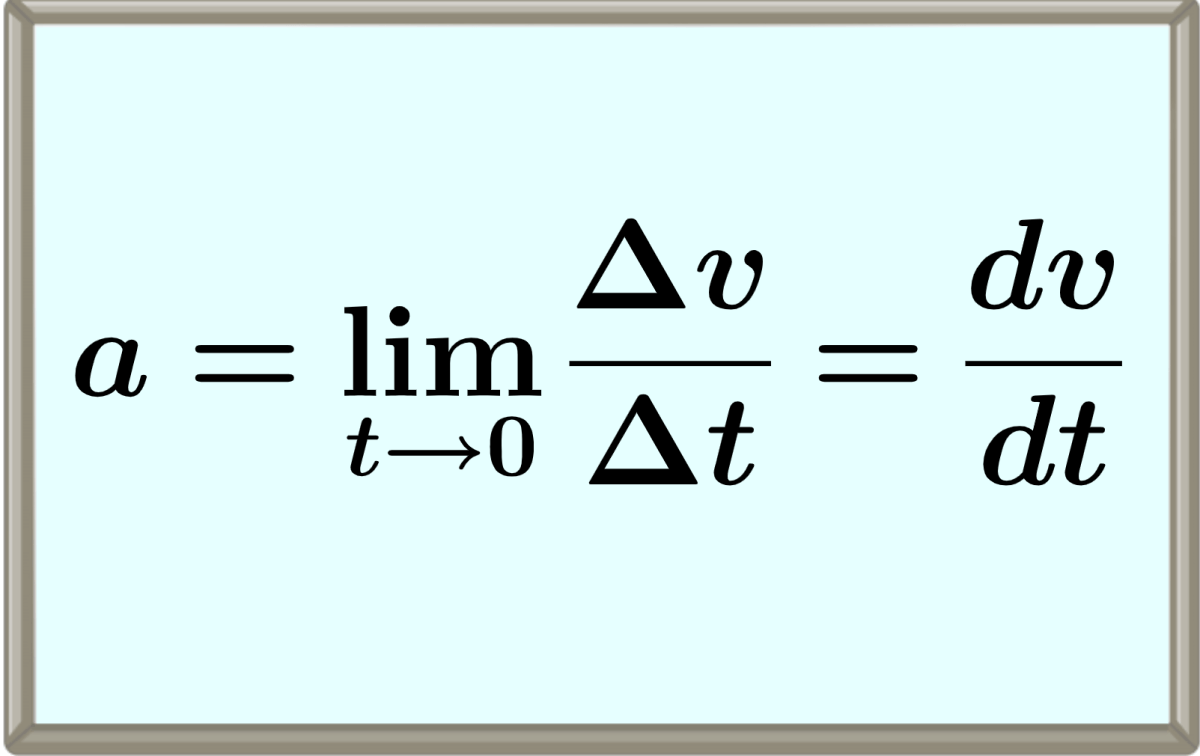La aceleración instantánea es una medida de cómo cambia la velocidad de un objeto en un instante de tiempo específico. Es el límite de la aceleración media en un intervalo infinitesimalmente pequeño a medida que ese intervalo se aproxima a cero.
Aunque a menudo hablamos de la aceleración como una tasa media, entender cómo puede cambiar en un instante dado nos da una visión más precisa y matizada del movimiento de un objeto. En este artículo analizaremos en detalle la aceleración instantánea. Exploraremos su fórmula y veremos algunos ejemplos.
¿Qué es la velocidad instantánea en física?
La aceleración instantánea describe la tasa de cambio de la velocidad de un objeto en un instante determinado. Es la aceleración que experimenta un objeto en un momento específico.
A diferencia de la aceleración media, que proporciona la tasa media de cambio de la velocidad en un intervalo de tiempo, la aceleración instantánea se centra en un punto concreto del tiempo para medir la rapidez con la que cambia la velocidad en ese preciso instante.
Es importante recordar que la aceleración, incluida la instantánea, es una magnitud vectorial. Esto significa que no sólo tiene magnitud, sino también dirección. La magnitud de la aceleración instantánea nos indica lo rápido que cambia la velocidad en un momento determinado, mientras que la dirección indica en qué sentido cambia la velocidad.
Matemáticamente, la aceleración instantánea se puede encontrar diferenciando la función de velocidad con respecto al tiempo. En el caso de una función de posición $latex s(t)$, primero encontramos la función de velocidad $latex v(t)$ diferenciando $latex s(t)$ con respecto al tiempo, y luego encontramos la función de aceleración $latex a(t)$ diferenciando $latex v(t)$ con respecto al tiempo.
Esto significa que la aceleración instantánea está estrechamente relacionada con los conceptos de velocidad y tasa de cambio, ideas básicas del cálculo. La aceleración instantánea consiste en comprender la tasa instantánea de cambio de la velocidad.
Fórmula y cálculo de la aceleración instantánea
La aceleración instantánea es el límite de la aceleración media a medida que el intervalo de tiempo se aproxima a cero. La fórmula de la aceleración instantánea se expresa como:
$$a(t)= \lim\limits_{\Delta t\to 0} \frac{ \Delta v}{ \Delta t}$$
$$a = \frac{dv}{dt}$$
donde:
- $latex a$ es la aceleración instantánea,
- $latex dv$ es el cambio en la velocidad, y
- $latex dt$ es el cambio en el tiempo.
Se trata esencialmente de la derivada de la velocidad con respecto al tiempo. El «$latex d$» en la fórmula denota un elemento diferencial, o un cambio infinitesimalmente pequeño. Así, $latex \frac{dv}{dt}$ se refiere al cambio en la velocidad ($latex dv$) por unidad de tiempo ($latex dt$).
Calcular la aceleración instantánea paso a paso
Veamos el proceso para hallar la aceleración instantánea.
Paso 1: Identifique la función de velocidad. Generalmente, suele ser una función en función del tiempo.
Paso 2: Diferencia la función velocidad. La función aceleración es igual a la derivada de la función velocidad con respecto al tiempo.
Paso 3: Sustituye el tiempo requerido. Por ejemplo, si quisiéramos hallar la aceleración instantánea en $latex t = 3$ segundos. Sustituimos $latex t = 3$ en nuestra función de aceleración.
El método descrito anteriormente nos permite determinar la aceleración instantánea en cualquier punto del tiempo, siempre que dispongamos de la función velocidad del objeto. Si, en cambio, tenemos la función de posición, necesitaríamos diferenciar dos veces para encontrar la función de aceleración.
Aceleración instantánea – Ejemplos con respuestas
Vamos a explorar algunos problemas relacionados con la aceleración instantánea. Estos ejemplos suponen que entiendes los fundamentos del cálculo.
EJEMPLO 1
Dada la función de velocidad de una partícula $latex v(t) = t^3 – 4t$ (en m/s), encuentra la aceleración instantánea en $latex t = 2$ segundos.
Solución
Empezamos por hallar la función de aceleración, $latex a(t)$. Para ello, tomamos la derivada de la función de velocidad:
$latex a(t) = \dfrac{dv}{dt} = 3t^2 – 4$
A continuación, sustituye $latex t = 2$ en la función de aceleración para encontrar la aceleración instantánea en ese momento:
$latex a(2) = 3(2)^2 – 4 = 8~ \text{m/s}^2$.
Por lo tanto, la aceleración instantánea en $latex t = 2$ s es 8 m/s².
EJEMPLO 2
Un objeto tiene la función de posición $latex s(t) = 3t^3 – 2t^2 + 4$ (en metros). ¿Cuál es su aceleración instantánea en $latex t=2$ segundos?
Solución
En primer lugar, tenemos que encontrar la función de velocidad, $latex v(t)$, tomando la derivada de la función de posición:
$latex v(t) = \dfrac{ds}{dt} = 9t^2 – 4t$
Luego, encontramos la función de aceleración, $latex a(t)$, tomando la derivada de la función de velocidad:
$latex a(t) = \dfrac{dv}{dt} = 18t – 4$
Por último, sustituye $latex t = 2$ en la función de aceleración para encontrar la aceleración instantánea en ese momento:
$latex a(2) = 18(2) – 4 = 32 ~\text{m/s}^2$
Por lo tanto, la aceleración instantánea en $latex t = 2$ s es 32 m/s².
EJEMPLO 3
Si un objeto tiene la función velocidad $latex v(t) = \sin(t) + t^2$ (en m/s), determina la aceleración instantánea en $latex t = \pi$ segundos.
Solución
Diferenciando la función velocidad, encontramos la función aceleración, $latex a(t)$:
$latex a(t) = \dfrac{dv}{dt} = \cos(t) + 2t$
A continuación, sustituye $latex t = \pi$ en la función de aceleración para hallar la aceleración instantánea en ese momento:
$latex a(\pi) = \cos(\pi) + 2\pi = -1 + 2\pi ~\text{m/s}^2$
Por lo tanto, la aceleración instantánea en $latex t = \pi$ s es $latex -1 + 2\pi$ m/s².
EJEMPLO 4
Encuentra la aceleración instantánea en $latex t=3$ segundos de un objeto que tiene la función de posición $latex s(t) = t^4 – 6t^2$ (en metros).
Solución
En primer lugar, encontramos la derivada de la función de posición para encontrar la función de velocidad, $latex v(t)$:
$latex v(t) = \dfrac{ds}{dt} = 4t^3 – 12t$
A continuación, derivamos la función de velocidad para encontrar la función de aceleración, $latex a(t)$:
$latex a(t) = \dfrac{dv}{dt} = 12t^2 – 12$
Por último, sustituye $latex t = 3$ en la función de aceleración para encontrar la aceleración instantánea en ese momento:
$latex a(3) = 12(3^2) – 12 = 96 ~\text{m/s}^2$
Así, la aceleración instantánea a $latex t = 3$ s es de 96 m/s².
Aplicaciones de la aceleración instantánea
La aceleración instantánea tiene una amplia gama de aplicaciones, especialmente en campos como la física y la ingeniería. He aquí algunos ejemplos:
Análisis del movimiento del vehículo: La aceleración instantánea de un auto o de cualquier vehículo puede utilizarse para estudiar y analizar su movimiento. Por ejemplo, comprender lo rápido que puede acelerar un vehículo es crucial para diseñar sistemas de frenado y predecir distancias de frenado.
Astronomía e ingeniería espacial: Cuando se lanzan naves espaciales o se estudian cuerpos celestes, el concepto de aceleración instantánea es clave. Se utiliza para calcular trayectorias de lanzamiento, maniobrar naves espaciales y comprender los movimientos de estrellas y planetas.
Deportes y biomecánica: Comprender la aceleración instantánea también es esencial en la ciencia del deporte. Ayuda a mejorar el rendimiento atlético, a diseñar programas de entrenamiento más eficaces, a prevenir lesiones e incluso a crear equipos más ergonómicos.
Robótica y automatización: en robótica, el concepto de aceleración instantánea se utiliza para controlar con precisión el movimiento de los robots. Es importante en aplicaciones que van desde la automatización industrial a los vehículos autónomos.
Veáse también
¿Quieres saber más sobre velocidad y aceleración? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
