Para resolver ecuaciones cuadráticas con el método de completar el cuadrado, tenemos que convertir a una ecuación de la forma ax2+bx+c a la forma a(x–h)2=k. Luego, podemos sacar la raíz cuadrada de ambos lados. Esto hará que podamos resolver para x fácilmente.
A continuación, aprenderemos a resolver ecuaciones cuadráticas completando el cuadrado. Veremos un proceso paso a paso y lo usaremos para resolver algunos ejercicios de práctica.
ÁLGEBRA
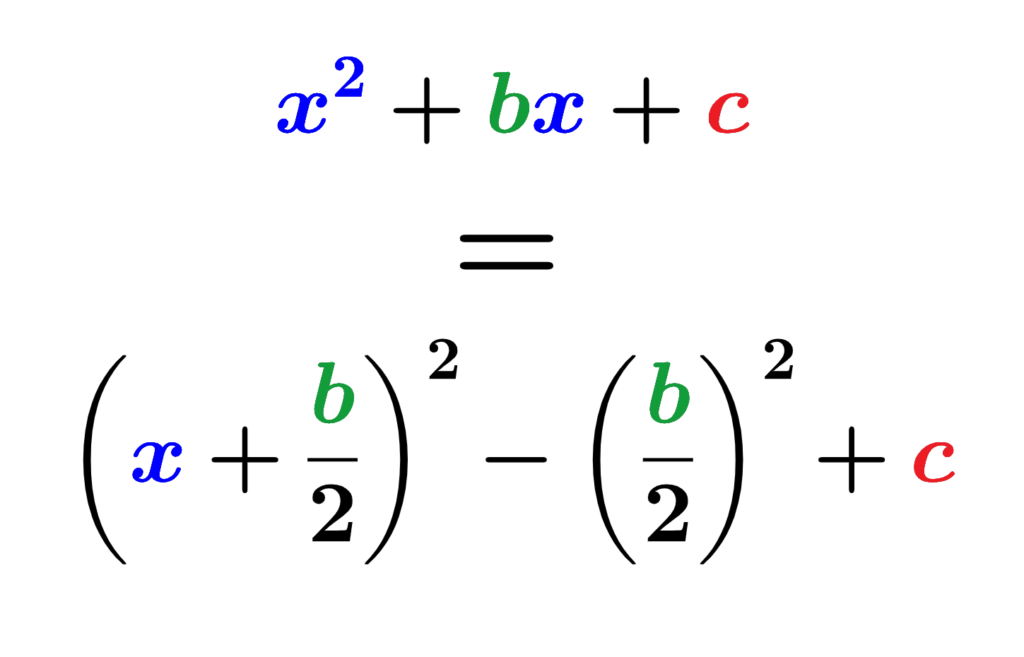
Relevante para…
Aprender a resolver ecuaciones cuadráticas completando el cuadrado.
ÁLGEBRA
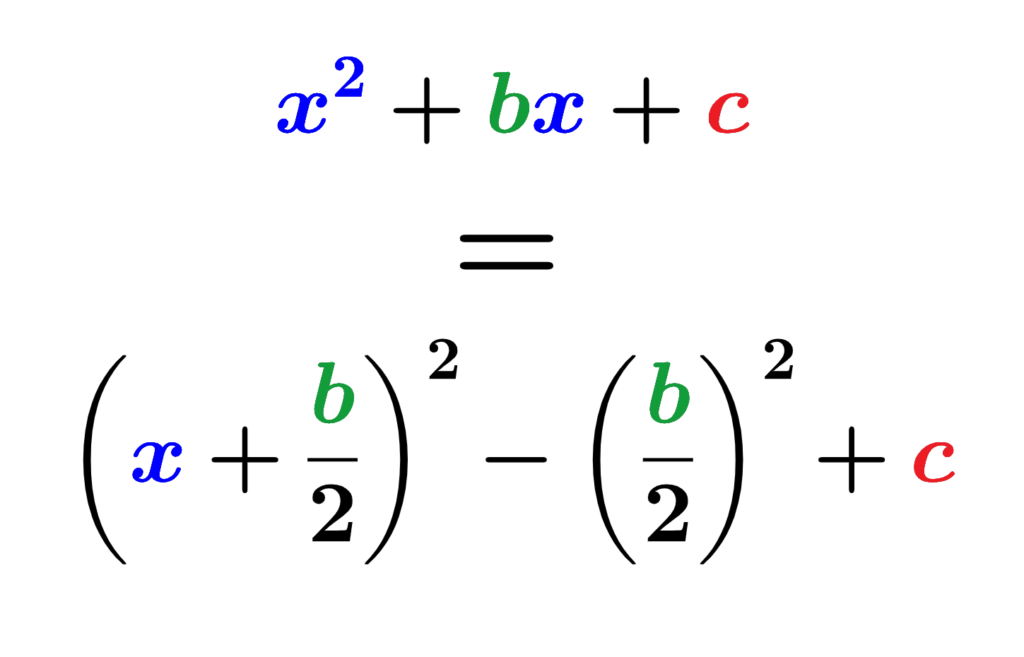
Relevante para…
Aprender a resolver ecuaciones cuadráticas completando el cuadrado.
Resolver ecuaciones cuadráticas completando el cuadrado – Método paso a paso
Para resolver ecuaciones cuadráticas a través del método de completar el cuadrado, podemos seguir los siguientes pasos asumiendo que empezamos con una ecuación escrita en la forma $latex ax^2+bx+c=0$.
Paso 1: Cuando el coeficiente del término cuadrático (a) es diferente de 1, dividimos a la ecuación cuadrática por a de modo que obtengamos una ecuación con un valor de a igual a 1:
$latex x^2+bx+c=0$
Paso 2: Tomamos al coeficiente b y lo dividimos por 2:
$$\left(\frac{b}{2}\right)$$
Paso 3: Tomamos la expresión del paso 2 y la elevamos al cuadrado:
$$\left(\frac{b}{2}\right)^2$$
Paso 4: Sumamos y restamos la expresión obtenida en el paso 3 a la ecuación obtenida en el paso 1:
$$x^2+bx+\left(\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Paso 5: Aplicamos la identidad $latex x^2+2xy+y^2=(x+y)^2$ para factorizar la ecuación cuadrática:
$$\left(x+\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c=0$$
Paso 6: Multiplicamos a la expresión resultante del paso 5 por el número por el que dividimos en el paso 1 y simplificamos para obtener una ecuación de la siguiente forma:
$latex (x-h)^2+k=0$
Paso 7: Escribimos a la ecuación de la siguiente forma:
$latex (x-h)^2=-k$
Paso 8: Sacamos la raíz cuadrada de ambos lados de la ecuación:
$latex x-h=\sqrt{-k}$
Paso 9: Las soluciones de la ecuación cuadrática son:
$latex x=h\pm \sqrt{-k}$
Resolver ecuaciones cuadráticas completando el cuadrado – Ejercicios resueltos
La técnica de completar el cuadrado es usada para resolver los siguientes ejercicios. Los pasos vistos arriba son aplicados pero en una forma más simplificada.
EJERCICIO 1
Completa el cuadrado de la expresión $latex x^2+2x-3=0$ y resuelve la ecuación.
Solución
Dado que el valor del coeficiente a es igual a 1, no tenemos que dividir a la ecuación por ningún número inicialmente.
El coeficiente b es igual a 2. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{2}{2}\right)^2=1$$
Al sumar y restar ese valor, tenemos:
$$x^2+2x-3=x^2+2x+1-1-3$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+1)^2-1-3$
$latex = (x+1)^2-4$
Ahora, podemos escribimos a la ecuación de la siguiente forma:
$latex (x+1)^2=4$
Y sacamos la raíz cuadrada de ambos lados:
⇒ $latex x+1=2~~$ o $latex ~~x+1=-2$
Resolviendo, tenemos:
⇒ $latex x=1~~$ o $latex ~~x=-3$
EJERCICIO 2
Resuelve la ecuación $latex x^2+4x-6=0$ usando el método de completar el cuadrado.
Solución
No tenemos que aplicar el primer paso, ya que el coeficiente del término es igual a 1.
Aquí, el coeficiente b es igual a 4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Al sumar y restar ese valor a la ecuación cuadrática, tenemos:
$$x^2+4x-6=x^2+4x+2^2-2^2-6$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+2)^2-4-6$
$latex = (x+2)^2-10$
Entonces, tenemos la ecuación:
$latex (x+2)^2=10$
Al sacar la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x+2=\sqrt{10}$
Resolviendo, tenemos:
⇒ $latex x=-2\pm \sqrt{10}$
EJERCICIO 3
Resuelve la ecuación cuadrática $latex x^2+6x-1=0$ al completar el cuadrado.
Solución
En esta ecuación, tenemos un coeficiente b igual a 3, entonces tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{6}{2}\right)^2$$
$$=3^2$$
Sumando y restando ese valor a la expresión cuadrática, tenemos:
$$x^2+6x-1=x^2+6x+3^2-3^2-1$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+3)^2-9-1$
$latex = (x+3)^2-10$
Para resolver la ecuación, la escribimos de la siguiente forma:
$latex (x+3)^2=10$
Sacando la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x+3=\sqrt{10}$
Resolviendo, tenemos:
⇒ $latex x=-3\pm \sqrt{10}$
EJERCICIO 4
Completa el cuadrado de la expresión $latex 2x^2+8x-10=0$ y resuelve la ecuación.
Solución
Empezamos dividiendo a la expresión por 2 para lograr que el coeficiente del término cuadrático sea igual a 1:
⇒ $latex x^2+4x-5=0$
Ahora, el coeficiente b es igual a 4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Sumando y restando a la expresión cuadrática, tenemos:
$$x^2+4x-5=x^2+4x+2^2-2^2-5$$
Completamos el cuadrado y simplificamos
$latex = (x+2)^2-4-5$
$latex = (x+2)^2-9$
Ahora, escribimos a la ecuación así:
⇒ $latex (x+2)^2=9$
Y sacamos la raíz cuadrada de ambos lados:
⇒ $latex x+2=3~~$ o $latex ~~x+2=-3$
Resolviendo, tenemos:
⇒ $latex x=1~~$ o $latex ~~x=-5$
EJERCICIO 5
Usa el método de completar el cuadrado para resolver la ecuación $latex x^2-3x+1=0$
Solución
El coeficiente b en esta ecuación es igual a -3. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{-3}{2}\right)^2$$
Sumado y restando esta expresión a la ecuación cuadrática, tenemos:
$$x^2-3x+1=x^2-2x+\left(\frac{-3}{2}\right)^2-\left(\frac{-3}{2}\right)^2+1$$
Al completar el cuadrado y simplificar, tenemos:
$latex = (x-\frac{3}{2})^2-\left(\frac{-3}{2}\right)^2+1$
$latex = (x-\frac{3}{2})^2-\frac{5}{4}$
Ahora, podemos escribimos a la ecuación de la siguiente forma:
$latex ⇒ (x-\frac{3}{2})^2=\frac{5}{4}$
Al sacar la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x-\frac{3}{2}=\sqrt{\frac{5}{4}}$
⇒ $latex x-\frac{3}{2}=\frac{\sqrt{5}}{2}$
Resolviendo, tenemos:
⇒ $latex x=\frac{3}{2}\pm \frac{\sqrt{5}}{2}$
EJERCICIO 6
Encuentra las soluciones a la ecuación $latex x^2+6x-7=0$ usando el método de completar el cuadrado.
Solución
En esta ecuación, el coeficiente b es igual a 6. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{6}{2}\right)^2$$
$$=3^2$$
Sumando esa expresión a la ecuación cuadrática, tenemos:
$$x^2+6x-7=x^2+6x+3^2-3^2-7$$
Al completar el cuadrado y simplificar, tenemos:
$latex = (x+3)^2-9-7$
$latex = (x+3)^2-16$
Ahora, podemos escribir a la ecuación de la siguiente forma:
$latex (x+3)^2=16$
Sacamos la raíz cuadrada de ambos lados para resolver:
$latex x+3=4~~$ o $latex ~~x+3=-4$
⇒ $latex x=1~~ $ o $latex ~~x=-7$
EJERCICIO 7
Resuelve la ecuación cuadrática $latex 3x^2+15x+15=0$ usando el método de completar el cuadrado.
Solución
Empezamos dividiendo a la ecuación por 3 para lograr que el coeficiente del término cuadrático sea igual a 1:
$latex x^2+3x+3=0$
Aquí, el coeficiente b es igual a 3. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{3}{2}\right)^2$$
Sumando y restando este valor a la expresión cuadrática, tenemos:
$$x^2+3x+3=x^2+3x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+3$$
Al completar el cuadrado y simplificar, tenemos:
$latex = (x+\frac{3}{2})^2-\frac{9}{4}+3$
$latex = (x+\frac{3}{2})^2+\frac{3}{4}$
Ahora, escribimos de la siguiente manera:
$latex = (x+\frac{3}{2})^2=-\frac{3}{4}$
Sacando la raíz cuadrada de ambos lados, tenemos:
$latex (x+\frac{3}{2})=\sqrt{-\frac{3}{4}}$
Dado que $latex \sqrt{-\frac{3}{4}}$ no es real, la ecuación no tiene raíces reales.
Resolver ecuaciones cuadráticas completando el cuadrado – Ejercicios para resolver
Usa la técnica de completar el cuadrado para resolver las siguientes ecuaciones cuadráticas. Haz clic en «Verificar» para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre completar el cuadrado? Puedes visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
