La técnica de completar el cuadrado es una técnica de factorización que nos permite convertir una expresión o ecuación cuadrática dada en la forma ax2+bx+c a la forma a(x–h)2+k. Podemos usar esta técnica para simplificar el proceso de resolución de ecuaciones cuando tenemos ecuaciones cuadráticas complejas.
A continuación, veremos un resumen sobre la técnica de completar el cuadrado. Usaremos esta técnica para resolver algunos ejercicios de práctica.
Fórmula para completar el cuadrado
El proceso de completar el cuadrado es usado para expresar una expresión cuadrática $latex ax^2+bx+c$ en la siguiente forma:
$latex a(x+p)^2+q$
en donde, p y q son constantes.
El caso más simple de completar el cuadrado sucede cuando tenemos que a=1, es decir, el término cuadrático tiene un coeficiente igual a 1. En estos casos, tenemos:
$$x^2+bx+c=\left(x+\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c$$
$$=\left(x+\frac{b}{2}\right)^2-\left(\frac{b^2}{4}\right)+c$$
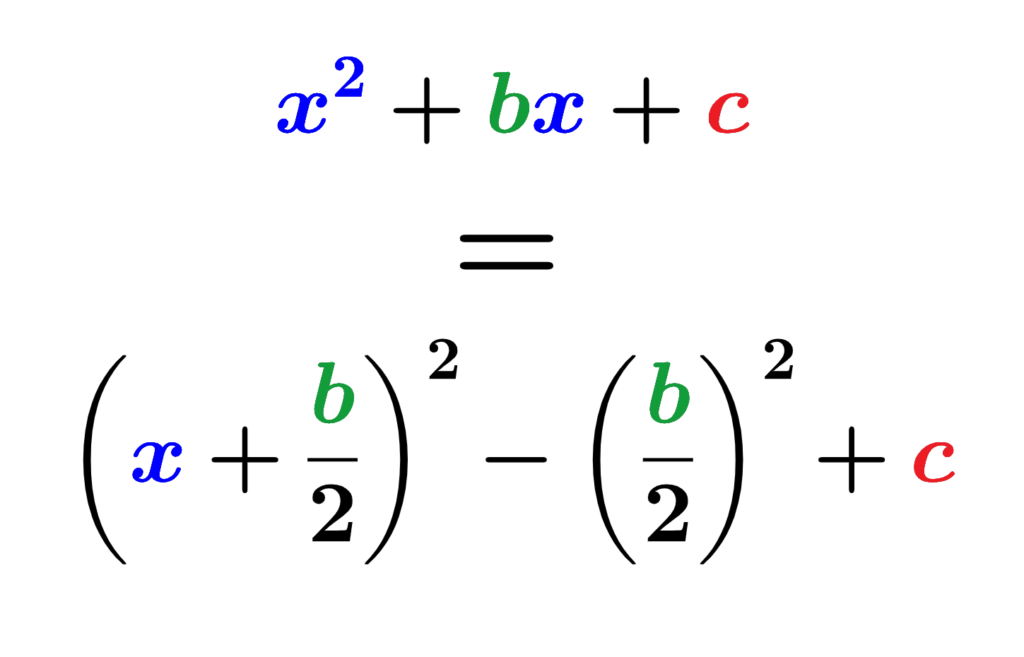
Completar el cuadrado – Método paso a paso
Podemos seguir los siguientes pasos para completar el cuadrado de una expresión cuadrática. Este método aplica incluso cuando el coeficiente a es diferente de 1.
Paso 1: Si es que el coeficiente a es diferente de 1, dividimos a toda la expresión cuadrática por a para obtener una expresión en donde el término cuadrático tiene un coeficiente igual a 1:
$latex x^2+bx+c$
Paso 2: Dividimos al coeficiente de x (el coeficiente b) por 2:
$$\left(\frac{b}{2}\right)$$
Paso 3: Elevamos al cuadrado a la expresión obtenida en el paso 2:
$$\left(\frac{b}{2}\right)^2$$
Paso 4: Sumamos y restamos la expresión obtenida en el paso 3 a la expresión obtenida en el paso 1:
$$x^2+bx+\left(\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c$$
Paso 5: Factorizamos la expresión cuadrática aplicando la identidad algebraica $latex x^2+2xy+y^2=(x+y)^2$:
$$\left(x+\frac{b}{2}\right)^2-\left(\frac{b}{2}\right)^2+c$$
Paso 6: Multiplicamos a la expresión resultante del paso 5 por el número por el que dividimos en el paso 1.
Resolver ecuaciones cuadráticas completando el cuadrado
El método de completar el cuadrado nos permite resolver ecuaciones cuadráticas fácilmente. Cuando tenemos una expresión cuadrática en la forma $latex (x-h)^2+k$, podemos escribirla de la siguiente forma:
$latex (x-h)^2=-k$
Aquí, podemos sacar la raíz cuadrada de ambos lados y fácilmente resolver para x.
Completar el cuadrado – Ejercicios resueltos
EJERCICIO 1
Completa el cuadrado de la expresión $latex x^2+2x-5$.
Solución
Dado que el coeficiente del término cuadrático es igual a 1, no tenemos que dividir a la expresión por ningún número inicialmente.
Vemos que el coeficiente b es igual a 2. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{2}{2}\right)^2=1$$
Al sumar y restar este valor, tenemos:
$$x^2+2x-5=x^2+2x+1-1-5$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+1)^2-1-5$
$latex = (x+1)^2-6$
EJERCICIO 2
Completa el cuadrado de la expresión $latex x^2+4x+10$.
Solución
No tenemos que aplicar el primer paso, ya que el coeficiente del término cuadrático es igual a 1.
Ahora, podemos ver que el coeficiente b es igual a 4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Cuando sumamos y restamos esta expresión, tenemos:
$$x^2+4x+10=x^2+4x+2^2-2^2+10$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+2)^2-4+10$
$latex = (x+2)^2+6$
EJERCICIO 3
Completa el cuadrado de la expresión $latex 2x^2+6x+6$.
Solución
Aquí, la expresión tiene un término cuadrático con un coeficiente diferente de 1. Entonces, podemos dividir a toda la expresión por 2 para obtener lo siguiente
⇒ $latex x^2+3x+3$.
Dado que el coeficiente b igual a 3, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{3}{2}\right)^2$$
Al sumar y restar este valor, tenemos:
$$x^2+3x+3=x^2+3x+\left(\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2+3$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+\frac{3}{2})^2-\frac{9}{4}+3$
$latex = (x+\frac{3}{2})^2+\frac{3}{4}$
Dado que dividimos a la expresión por 2 inicialmente, multiplicamos el resultado por 2:
⇒ $latex 2(x+\frac{3}{2})^2+\frac{3}{2}$
EJERCICIO 4
Resuelve la ecuación $latex x^2+4x-5=0$ usando el método de completar el cuadrado.
Solución
En esta ecuación, b es igual a 4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{4}{2}\right)^2$$
$$=2^2$$
Sumado y restando este valor a la ecuación cuadrática, tenemos:
$$x^2+4x-5=x^2+4x+2^2-2^2-5$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+2)^2-4-5$
$latex = (x+2)^2-9$
Ahora, podemos escribir a la ecuación de la siguiente manera:
⇒ $latex (x+2)^2=9$
Sacando la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x+2=\sqrt{9}$
⇒ $latex x+2=3$
⇒ $latex x=1$
EJERCICIO 5
Resuelve la ecuación $latex 2x^2-8x-8=0$ usando el método de completar el cuadrado.
Solución
Dividimos a la ecuación por 2 para obtener una ecuación en donde el coeficiente del término cuadrático es igual a 1:
$latex x^2-4x-4=0$
Ahora, vemos que el coeficiente b es igual a -4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{-4}{2}\right)^2$$
$$=(-2)^2$$
Sumando y restando ese valor a la ecuación, tenemos:
$$x^2-4x-4=x^2-4x+(-2)^2-(-2)^2-4$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x-2)^2-4-4$
$latex = (x-2)^2-8$
Ahora, escribimos a la ecuación de la siguiente forma:
⇒ $latex (x-2)^2=8$
Sacando la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x-2=\sqrt{8}$
⇒ $latex x=2\pm \sqrt{8}$
EJERCICIO 6
Encuentra las soluciones de la ecuación $latex 2x^2+12x-14=0$ usando el método de completar el cuadrado.
Solución
Dividiendo a la ecuación por 2, podemos lograr que el coeficiente del término cuadrático sea igual a 1:
⇒ $latex x^2+6x-7=0$
Ahora, tenemos que el coeficiente b es igual a 6. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{6}{2}\right)^2$$
$$=3^2$$
Si es que sumamos y restamos este valor a la ecuación, tenemos:
$$x^2+6x-7=x^2+6x+3^2-3^2-7$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x+3)^2-9-7$
$latex = (x+3)^2-16$
Podemos escribir a la ecuación de la siguiente forma:
$latex (x+3)^2=16$
Sacando la raíz cuadrada de ambos lados, tenemos:
⇒ $latex x+3=4$
⇒ $latex x=1$
EJERCICIO 7
Resuelve la ecuación cuadrática $latex 3x^2-12x-3=0$ usando el método de completar el cuadrado.
Solución
Empezamos dividiendo a la ecuación por 3 para lograr que el coeficiente del término cuadrático sea igual a 1:
⇒ $latex x^2-4x-1=0$
Vemos que el coeficiente b es igual a -4. Entonces, tenemos:
$$\left(\frac{b}{2}\right)^2=\left(\frac{-4}{2}\right)^2$$
$$=(-2)^2$$
Al sumar y restar este valor a la ecuación, tenemos:
$$x^2-4x-1=x^2-4x+(-2)^2-(-2)^2-1$$
Completando el cuadrado y simplificando, tenemos:
$latex = (x-2)^2-4-1$
$latex = (x-2)^2-5$
Podemos escribir a la ecuación de la siguiente forma:
$latex (x-2)^2=5$
Podemos resolver la ecuación al sacar la raíz cuadrada de ambos lados:
⇒ $latex (x-2)=\sqrt{5}$
⇒ $latex x=2\pm \sqrt{5}$
Completar el cuadrado – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre completar el cuadrado? Puedes visitar estas páginas:


