Los elementos más importantes de los sólidos platónicos son las caras, los vértices y las aristas. Además, también tenemos elementos adicionales secundarios como los ejes de simetría y las secciones transversales.
A continuación, haremos una revisión de los cinco sólidos platónicos y conoceremos a sus elementos principales y secundarios en detalle.
Caras de los sólidos platónicos
Las caras de los sólidos platónicos son las superficies planas formadas en los límites de los sólidos platónicos. Los sólidos platónicos tienen la característica principal de que todas sus caras son congruentes, es decir, tienen la misma forma y tamaño.
Además, las caras de los cinco sólidos platónicos son regulares. Dependiendo del sólido platónico, tenemos diferentes números de caras y diferentes formas. Entonces, tenemos:
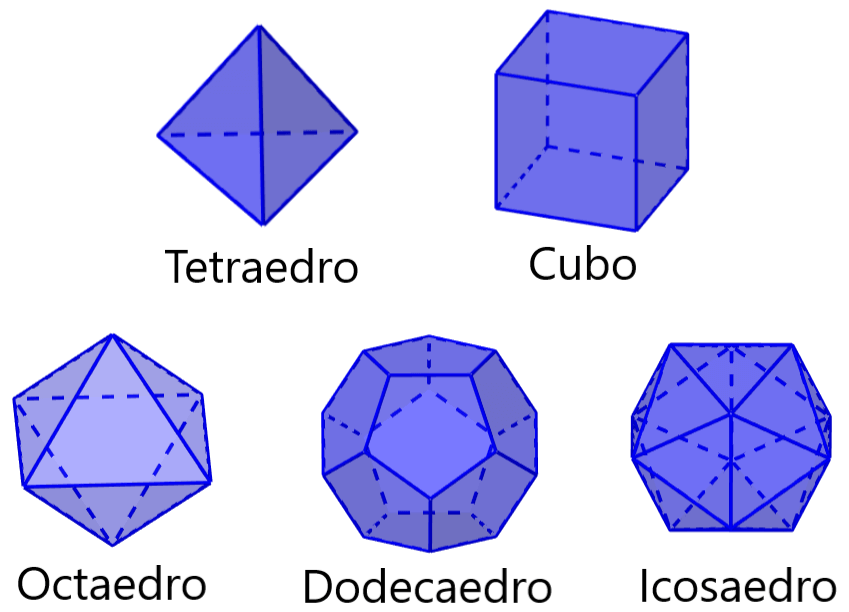
- Un tetraedro tiene 4 caras triangulares.
- Un cubo tiene 6 caras cuadradas.
- Un octaedro tiene 8 caras triangulares.
- Un dodecaedro tiene 12 caras pentagonales.
- Un icosaedro tiene 20 caras triangulares.
En el caso de los tetraedros, octaedros e icosaedros, las caras son triangulares, por lo que cada cara está formada por tres aristas. Además, cada cara está rodeada de otras tres caras.
En el caso de los cubos, cada cara está formada por cuatro aristas y está rodeada de otras cuatro caras. Y en el caso de los dodecaedros, cada cara está formada por cinco aristas y está rodeada de otras cinco caras.
El área superficial de los sólidos platónicos es encontrada al sumar las áreas de todas sus caras. Eso significa que si es que conocemos el área de una de las caras, simplemente tenemos que multiplicar por el número total de caras.
Vértices de los sólidos platónicos
Los vértices de los sólidos platónicos son los puntos en donde se encuentran las aristas. En general, los vértices son definidos como los puntos en donde se encuentran dos o más segmentos de líneas. Entonces, tenemos:
- Un tetraedro tiene 4 vértices.
- Un cubo tiene 8 vértices.
- Un octaedro tiene 6 vértices.
- Un dodecaedro tiene 20 vértices.
- Un icosaedro tiene 12 vértices.
El número de aristas que se encuentran en cada vértice no solo depende de la forma de las caras, sino también del tipo de sólido platónico. Por ejemplo, los tetraedros, los octaedros y los icosaedros tienen caras triangulares, pero un número diferente de aristas intersecan en cada vértice en las tres figuras.
- 3 aristas de un tetraedro intersecan en cada vértice.
- 3 aristas de un cubo intersecan en cada vértice.
- 4 aristas de un octaedro intersecan en cada vértice.
- 3 aristas de un dodecaedro intersecan en cada vértice.
- 5 aristas de un icosaedro intersecan en cada vértice.
Aristas de los sólidos platónicos
Las aristas de los sólidos platónicos son los segmentos de líneas que rodean a cada una de sus caras. En general, podemos definir a las aristas como los segmentos de líneas formados al unir a dos vértices.
Alternativamente, podemos considerar a las aristas como los segmentos de líneas en donde dos caras de los sólidos platónicos se encuentran. Cada sólido platónico tiene un número diferente de aristas. Entonces, tenemos:
- Un tetraedro tiene 6 aristas.
- Un cubo tiene 12 aristas.
- Un octaedro tiene 12 aristas.
- Un dodecaedro tiene 30 aristas.
- Un icosaedro tiene 30 aristas.
Ejes de simetría
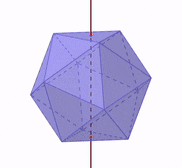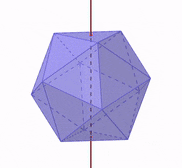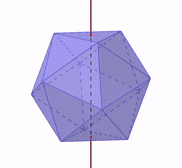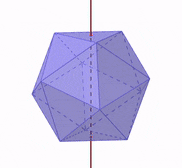
El eje de simetría es una línea vertical que divide a la figura en dos partes iguales. En el caso de los sólidos platónicos, el eje de simetría es una línea que pasa por el medio geométrico.
Si es que rotamos al sólido platónico con respecto a su eje de simetría, obtenemos una figura equivalente desde diferentes ángulos, como se muestra en la siguiente figura:
Secciones transversales
Las secciones transversales son las figuras bidimensionales formadas cuando una figura 3D es cortada por un plano. En el caso de los sólidos platónicos, podemos obtener diferentes secciones transversales dependiendo en cómo cortemos a la figura.
Por ejemplo, si es que cortamos a un cubo con un plano que es paralelo a las bases, podemos obtener una sección transversal cuadrada como se muestra en la figura.
En el caso de un tetraedro, podemos formar una sección transversal triangular si es que cortamos al sólido con un plano paralelo a su base.
En el caso de un octaedro, formaremos una sección transversal cuadrada al cortar al sólido con un plano que sea perpendicular a su eje de simetría.
Los dodecaedros y los icosaedros tienen secciones transversales más complejas, ya que están formados por un número mayor de caras. Entonces, la sección transversal variará dependiendo no solo del ángulo, sino de la altura en donde cortemos a las figuras.
Véase también
¿Interesado en aprender más sobre sólidos platónicos y figuras geométricas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
