La regla del trapecio es un método de aproximación a la integral definida de una función. Se basa en la idea de aproximar el área bajo una curva mediante una serie de trapecios en lugar de rectángulos, lo que proporciona una estimación más precisa.
A continuación, veremos un resumen de cómo usar la regla del trapecio para calcular integrales. Además, resolveremos varios ejercicios de práctica para aplicar este concepto.
Cómo usar la regla del trapecio para resolver integrales
Para utilizar la regla del trapecio para resolver integrales definidas, tienes que seguir estos pasos:
Paso 1: Divide el intervalo de integración [a, b] en $latex n$ subintervalos de igual anchura $latex h = \frac{b – a}{n}$.
Paso 2: Evalúa la función $latex f(x)$ en los puntos extremos de cada subintervalo, es decir, en $latex x = a,$ $latex a + h$, $latex a + 2h$, …, $latex a + (n-1)h$, y $latex b$.
Paso 3: Calcula la altura de cada trapecio tomando la media de los valores de la función en los extremos del subintervalo, es decir, $latex \frac{f(a) + f(a+h)}{2}$, $latex \frac{f(a+h) + f(a+2h)}{2}$, …, $latex \frac{f(a+(n-1)h) + f(b)}{2}$.
Paso 4: Calcula el área de cada trapecio multiplicando la altura por la anchura, es decir, $latex \frac{f(a) + f(a+h)}{2} \times h$, $latex \frac{f(a+h) + f(a+2h)}{2} \times h$, …, $latex \frac{f(a+(n-1)h) + f(b)}{2} \times h$.
Paso 5: Suma las áreas de todos los trapecios para obtener la aproximación de la integral definida de la función $latex f(x)$ sobre el intervalo [a, b].
Alternativamente, podemos usar la siguiente fórmula:
$$I_a = \frac{\Delta x}{2} ( f(x_0)+2[ f(x_1)+f(x_2)+f(x_3)+f(x_4) ]+f(x_5)$$
Cuanto menor sea el valor de $latex n$, menos precisa será la aproximación, pero utilizar un valor mayor de $latex n$ requerirá un proceso más largo.
Por lo tanto, es importante encontrar un equilibrio entre precisión y eficiencia cuando se utiliza la regla trapezoidal para la integración.
Ejercicios resueltos de regla del trapecio para aproximar integrales
EJERCICIO 1
Hallar el valor aproximado, mediante la regla del trapecio, de la siguiente integral definida:
$$ I= \int_{-2}^{2} \exp (-x^{2}) dx $$
Solución
Se sabe que una integral definida representa el área bajo la curva de la función matemática entre los límites de integración. Cuando es posible, esta área puede obtenerse calculando la integral indefinida y evaluándola entre los límites de integración.
Hay casos en que este procedimiento no es posible, como es el caso del presente ejemplo. Entonces se recurre a métodos numéricos aproximados.
El método de los trapecios consiste en dividir el intervalo de integración en n subintervalos y aproximar el área de cada uno por la del trapecio entre los puntos de las abscisas y las coordenadas de la función evaluada en esos valores.
De este modo se obtiene la integral aproximada $latex I_a$ mediante la siguiente fórmula, para el caso de $latex n$ intervalos regulares de ancho $latex h=\Delta x $.
$$ I_{a}=\frac{1}{2}\Delta x (f(x_{0})+2(f(x_{1})+f(x_{2})+…..+f(x_{n-2})+f(x_{n-1}))+f(x_{n})) $$
Ilustraremos el método eligiendo 5 subintervalos y mostrando detalladamente los cálculos. Es claro que si se quiere un resultado más preciso es necesario un número mayor de subintervalos.
- $latex f(x)=exp(-x^2)$
- $latex n=5$
- $latex a=-2$
- $latex b=+2$
- $latex h= \Delta x=\frac{b-a}{n} : 0.8$
Entonces, tenemos los siguientes valores de x:
- $latex x_{0}=a= -2.0$
- $latex x_{1}=a+\frac{1(b-a)}{n}= -1. 2$
- $latex x_{2}=a+\frac{2(b-a)}{n}= -0.4$
- $latex x_{3}=a+\frac{3(b-a)}{n}= 0.4$
- $latex x_{4}=a+\frac{4(b-a)}{n}= 1. 2$
- $latex x_{5}=a+\frac{5(b-a)}{n}= 2.0$
Usando estos valores encontramos los valores de la función o la altura:
- $latex f(x_{0})= 1. 8316×10^{-2}$
- $latex f(x_1)= 0.23693$
- $latex f(x_2)= 0.85214$
- $latex f(x_3)= 0.85214$
- $latex f(x_4)= 0.23693$
- $latex f(x_5)= 1. 8316×10^{-2}$
Por último, usamos la siguiente fórmula:
$$I_a=\frac{h}{2} (f(x_{0})+2(f(x_{1})+f(x_2)+f(x_3)+f(x_4))+f(x_5))= 1. 7572$$
Tomando un valor más preciso de la integral como lo es: I=1.7642, que se obtuvo mediante el uso de muchos más intervalos podemos estimar el error de nuestra aproximación de 5 subintervalos.
Error porcentual: $latex \left( \frac{I-I_a}{I}\right) ×100 =0.40%$
EJERCICIO 2
Usar la regla del trapecio para hallar un valor aproximado de la siguiente integral definida:
$$I=\int_{0}^{2} \sqrt{x} dx $$
(nota: usar 5 subintervalos)
Solución
Tenemos la siguiente información:
- $latex f(x)=\sqrt{x}$
- $latex n=5$
- $latex a=0$
- $latex b=2$
- $latex \Delta x=\frac{b-a}{n} = 0.4$
Entonces, podemos obtener los siguientes valores de x:
- $latex x_0=a= 0.0$
- $latex x_1=a+1\times \Delta x= 0.4$
- $latex x_2=a+2\times \Delta x= 0.8$
- $latex x_3=a+3\times \Delta x= 1. 2$
- $latex x_4=a+4\times \Delta x= 1. 6$
- $latex x_5=a+5\times \Delta x= 2.0$
Usando estos valores, encontramos las siguientes alturas:
- $latex f(x_0)= 0.0$
- $latex f(x_1)= 0.63246$
- $latex f(x_2)= 0.89443$
- $latex f(x_3)= 1. 0954$
- $latex f(x_4)= 1. 2649$
- $latex f(x_5)= 1. 4142$
El valor aproximado de la integral ($latex I_a$) se obtiene mediante la fórmula de la regla del trapecio:
$$I_a = \frac{\Delta x}{2} ( f(x_0)+2[ f(x_1)+f(x_2)+f(x_3)+f(x_4) ]+f(x_5)$$
$$I_a = 1. 84$$
La integral exacta es:
$$I=\int_{0}^{2} \sqrt{x} dx = \frac{4}{3} \sqrt{2} = 1.8856 $$
Error porcentual: $latex \frac{I-I_a}{I} \times 100 = 2.4% $
EJERCICIO 3
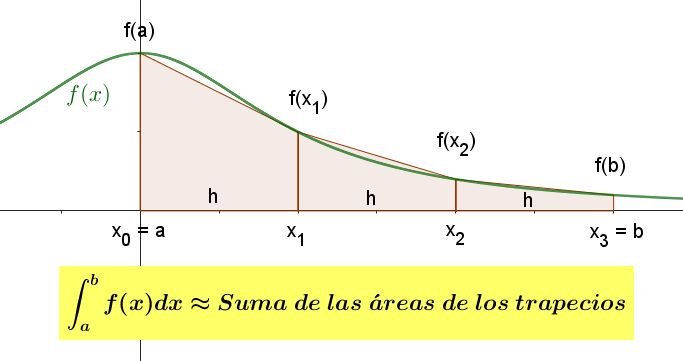
Sea la función f(x) mostrada en la figura. Encuentre una fórmula que dé, en forma aproximada, la integral definida de dicha función en el intervalo [a, b], tomando en cuenta que la suma del área de los trapecios allí representados, es numéricamente cercana al valor del área bajo la curva de la función.
Solución
Comenzaremos por recordar que un trapecio es un cuadrilátero con dos lados paralelos, a los cuales se les llama base. La separación o distancia entre las dos bases de un trapecio se les llama altura.
Por otra parte, se sabe que el área de un trapecio se calcula multiplicando la semisuma (suma divida entre 2) de la longitud de sus bases por su altura.
En el primer trapecio de la figura, la longitud de la base mayor es $latex f(a)$ y la longitud de la base menor es $latex f(x_1)$. La altura es la separación entre las bases, es decir $latex h$. Entonces el área del trapecio 1 es:
$$A_1 = \frac{f(a) + f(x_1)}{2} \cdot h $$
Similarmente, el área del trapecio 2 está dada por:
$$A_2 = \frac{f(x_1) + f(x_2)}{2} \cdot h $$
y la del trapecio 3 es:
$$A_3 = \frac{f(x_2) + f(b)}{2} \cdot h $$
El área total, es la suma del área de los tres trapecios que llamaremos $latex Sum $.
$$ Sum = \frac{f(a) + f(x_1)}{2} \cdot h + \frac{f(x_1) + f(x_2)}{2} \cdot h + \frac{f(x_2) + f(b)}{2} \cdot h $$
Nos damos cuenta que, en esta suma $latex \frac{h}{2} $ es factor común:
$$ Sum = \frac{h}{2} [f(a) + f(x_1) + f(x_1) + f(x_2) + f(x_2) + f(b)] $$
$$ Sum = \frac{h}{2} [f(a) + 2 \cdot f(x_1) + 2 \cdot f(x_2)] + f(b) $$
$$ Sum = \frac{h}{2} [f(a) + 2 [f(x_1) + f(x_2)] + f(b)] $$
Es decir que el valor de la integral definida puede aproximarse, en el caso n=3, por:
$$ \int_a^b f(x) dx \approx \frac{h}{2} [f(x_0) + 2 [f(x_1) + f(x_2)] + f(x_3)] $$
EJERCICIO 4
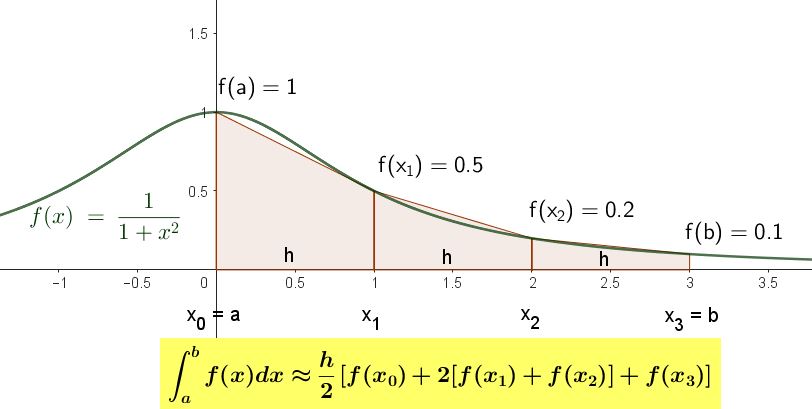
En la figura siguiente se muestra el gráfico de la función $latex f(x)= \frac{1}{1+x^2}$. Encontrar, con los datos de la figura, el valor aproximado de la integral definida:
$$ \int_0^3 \frac{1}{1+x^2} dx $$
Compare el resultado obtenido con el del valor exacto y estime el error porcentual de la aproximación.
Solución
Se hallará una aproximación a la integral definida dada mediante el uso de la fórmula para la regla de los trapecios para el caso de tres subintervalos, es decir n=3.
$$ \int_a^b f(x) dx \approx \frac{h}{2} [f(x_0) + 2 [f(x_1) + f(x_2)] + f(x_3)] $$
Sustituimos los valores que corresponden a este ejercicio:
$$ \int_0^3 \frac{1}{1+x^2} dx \approx \frac{1}{2} [1 + 2 [0.5 + 0.2] + 0.1] = 1.25 $$
Esta integral puede calcularse en forma analítica exacta:
$$ \int_0^3 \frac{1}{1+x^2} dx = \left |Arctan(x) \right |_0^3 = Arctan(3)-Arctan(0) = 1.24905 $$
El error porcentual de nuestra aproximación es:
$$ \frac{1.25-1.24905}{1.24905} \times 100 = 0.08 \% $$
Lo que demuestra que si la función tiene variación suave en el intervalo de integración, se puede conseguir resultados precisos con el método del trapecio, incluso tomando pocas subdivisiones.
EJERCICIO 5
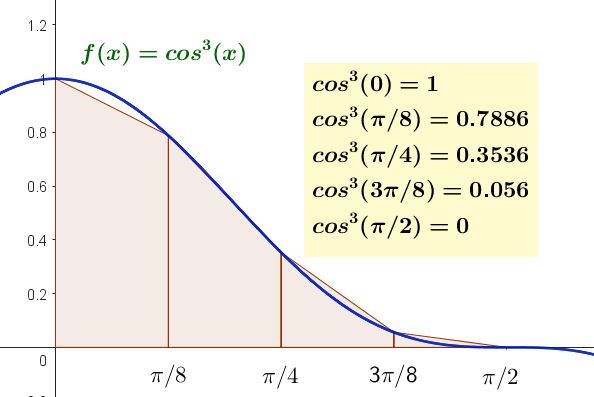
Encontrar una solución aproximada a la integral:
$$ \int_0^{\pi /2} cos^3(x) dx $$
aplicando la regla de los trapecios y tomando cuatro subdivisiones, es decir n=4.
Solución
La fórmula para la regla de los trapecios para el caso de cuatro subintervalos (n=4) es:
$$ \int_0^{\pi /4} f(x) dx \approx \frac{h}{2} [f(x_0) + 2 [f(x_1) + f(x_2)+f(x_3)] + f(x_4)] $$
Los valores de la función $latex f(x)=cos^3(x)$ en los extremos de los subintervalos se muestran en la figura del enunciado:
$$ \int_0^{\pi /4} f(x) dx \approx \frac{\pi /8}{2} [1 + 2 [0.7886 + 0.3536 + 0.056] + 0.0] = 0.6669 $$
El resultado exacto de esta integral es: 2/3= 0.66667
El error porcentual de la aproximación es:
$$ \frac{0.6669-0.66667}{0.66667} \times 100 = 0.03 \% $$
EJERCICIO 6
Hallar el valor de la integral indicada
$$ \int_0^{\pi /4} sec(x) dx $$
mediante la regla de los trapecios y tomando tres subdivisiones, es decir n=3.
Solución
Realizando una gráfica de la función y dividiendo en tres trapecios, obtenemos lo siguiente:
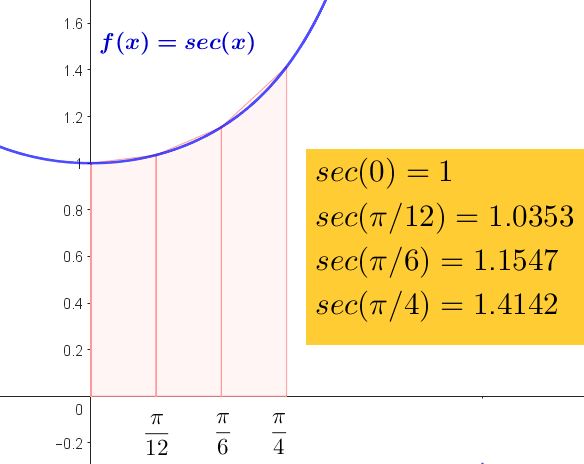
Entonces, usamos la fórmula de la regla del trapecio para encontrar el valor de la integral:
$$ I_a = \frac{\pi /12}{2} [sec(0) + 2 [sec( \pi /12) + sec( \pi /6))] + sec( \pi /4)]=0.889 $$
EJERCICIO 7
Mediante la suma de las areas de trapecios encuentre un valor aproximado de la integral indicada
$$ \int_{-4}^{+4} \frac{4}{2+x^4} dx $$
Usar nueve subdivisiones (n=9). Presentar las operaciones en forma de tabla y resaltando en color verde el resultado final.
Solución
Se usará la fórmula de la sumatoria de trapecios:
$$ I_a=\frac{h}{2} (f(x_{0})+2(f(x_{1})+f(x_{2})+…..+f(x_{n-2})+f(x_{n-1}))+f(x_{n})) $$
con n=9 y siendo la función $latex \frac{4}{2+x^4} $.
Los cálculos intermedios y el resultado final (resaltado en verde) se muestra en la siguiente tabla:
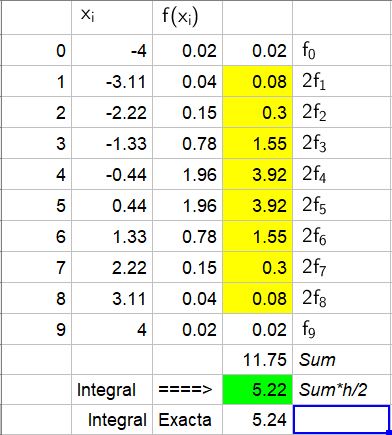
El valor obtenido mediante la aproximación de trapecios es 5.22, mientras que el valor exacto es 5.24
EJERCICIO 8
Aplique la regla de la suma de trapecios para encontrar una cuadratura (integral definida) de la siguiente función, en el intervalo [-4, 4]:
$$ f(x) = \frac{2}{\sqrt{1+x^2}} $$.
Nota: Usar n=8 y mostrar los resultados de las operaciones en una tabla. Resaltar en verde el resultado de la cuadratura.
Solución
El paso h se calcula mediante: $latex h= \frac{b-a}{n}= \frac{4-(-4)}{8}=1$.
Entonces, obtenemos los 8 valores de x y sus correspondientes valores de la función. Luego, usamos la fórmula de la regla de los trapecios:
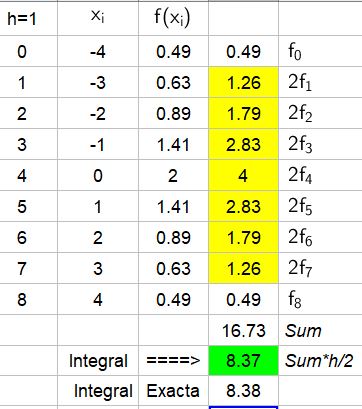
El valor de la integral es 8.37.
EJERCICIO 9
Mediante la regla de la suma de trapecios encuentre una aproximación a la integral definida de la siguiente función, en el intervalo [-4, 4]:
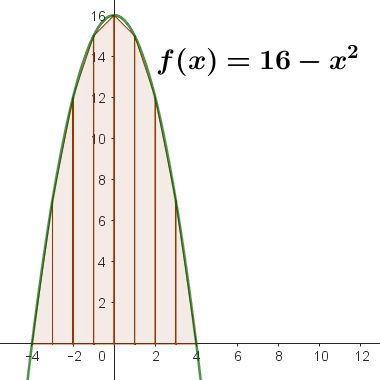
Nota: Usar n=8 y mostrar los resultados de las operaciones en una tabla. Resaltar en verde el resultado de la cuadratura.
Solución
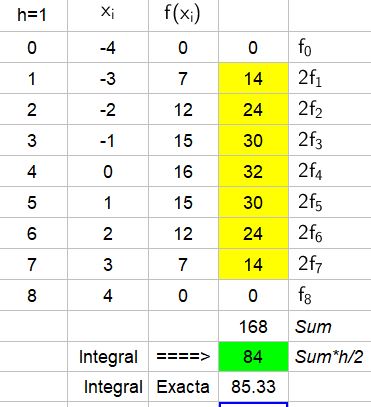
La distancia entre el límite inferior $latex x=-4$ y el límite superior $latex x=4$ es 8, por lo que al dividir por los 8 intervalos, tenemos $latex h=1$.
Entonces, determinamos los valores de x y sus «alturas» correspondientes, para luego usar la regla de los trapecios:
EJERCICIO 10
Halle la integral definida entre -4 y 4, mediante aproximación de suma de trapecios para la función mostrada. Por cierto, esta es la función que describe una cuerda o cadena colgando entre dos puntos fijos, razón por la cual se le conoce como catenaria.
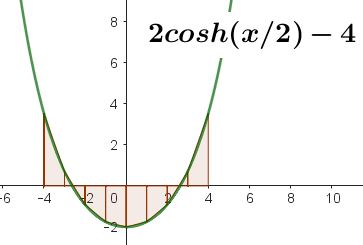
Nota: Usar n=8 y mostrar los resultados de las operaciones en una tabla. Resaltar en verde el resultado de la cuadratura.
Solución
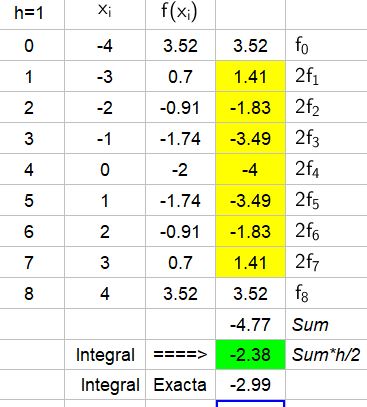
Similar al ejercicio anterior, el valor de $latex h$ es 1, ya que la distancia entres los límites de integración es 8 y tenemos 8 intervalos.
La siguiente tabla muestra los valores de x, sus valores de f correspondientes y el resultado de aplicar la regla del trapecio:
Ejercicios de regla del trapecio para resolver


Usa la regla del trapecio con 4 subintervalos o trapecios para encontrar un valor aproximado para:$$\int_{1}^{9}\sqrt{\ln(x)}dx$$
Escribe la respuesta a dos lugares decimales.
Véase también
¿Interesado en aprender más sobre métodos numéricos? Puedes mirar estas páginas:


