Los determinantes son un concepto fundamental del álgebra lineal. Para calcular el determinante de una matriz de 3×3, multiplicamos a cada elemento de la fila superior por el determinante de la matriz de 2×2 formada al eliminar su fila y columna, luego alterna los signos y suma los resultados.
A continuación, conoceremos cómo encontrar el determinante de una matriz 3×3 paso a paso. Veremos varios ejercicios de práctica para aplicar lo aprendido.
ÁLGEBRA
Relevante para…
Aprender sobre el determinante de matrices 3×3 con ejercicios.
ÁLGEBRA
Relevante para…
Aprender sobre el determinante de matrices 3×3 con ejercicios.
¿Cómo encontrar el determinante de una matriz 3×3?
El método general para encontrar el determinante de una matriz de 3×3 consiste en utilizar el método de expansión cofactorial, también conocido como expansión de Laplace.
Los siguientes son los pasos que podemos seguir para aplicar este método:
Paso 1: Elegir una fila o columna (normalmente se elige la primera fila para simplificar) de la matriz 3×3.
Paso 2: Para cada elemento de la fila o columna elegida, hallar el menor correspondiente. El menor es el determinante de la matriz 2×2 que queda después de eliminar la fila y la columna que contienen al elemento actual.
Por ejemplo, si tomamos la primera fila, tendríamos
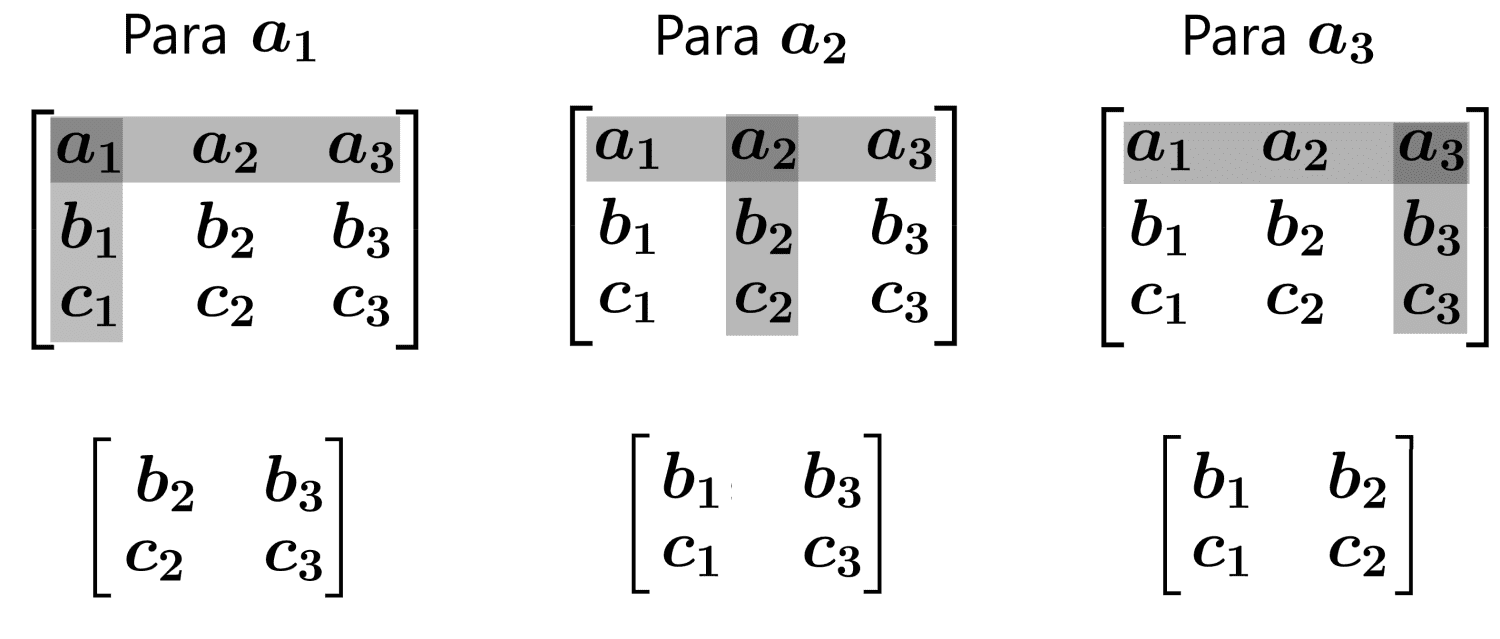
Paso 3: Multiplica cada elemento de la fila o columna elegida por su menor correspondiente.
Paso 4: Alternar los signos de los productos resultantes usando el siguiente diagrama.
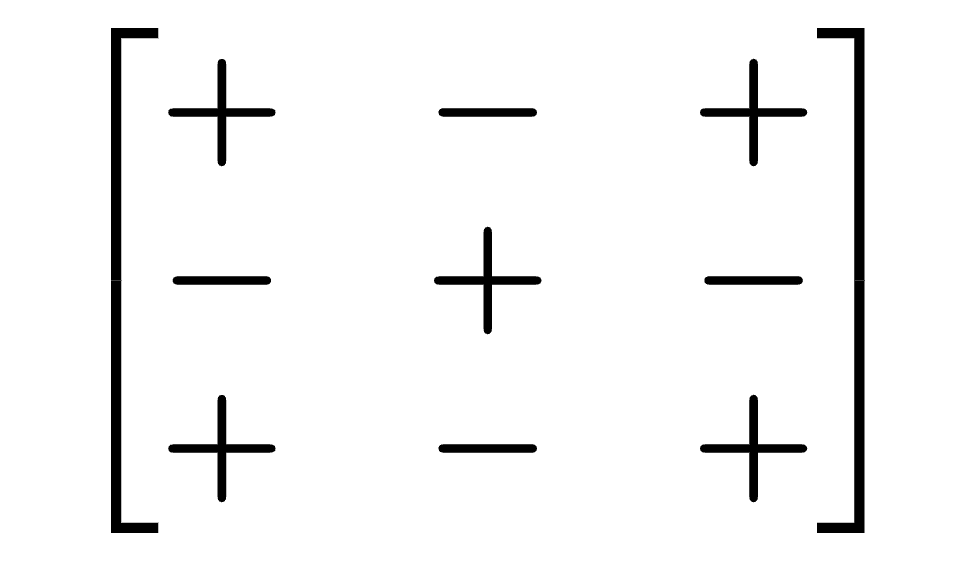
Por ejemplo, si tomamos la primera fila, los signos serán +, -, +. Si tomamos la segunda fila, los signos serán -, +, -.
Paso 5: Suma los productos para obtener el determinante de la matriz 3×3.
Ahora, apliquemos estos pasos en la matriz general A:
$$A=\begin{bmatrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{bmatrix}$$
Vamos a usar la primera fila de la matriz. Entonces, multiplicamos a cada elemento por su menor y usamos los signos +, -, +.
$$\det(A) = a_{1} \cdot \det(\text{Menor}_{a_{1}}) – a_{2} \cdot \det(\text{Menor}_{a_{2}}) + a_{3} \cdot \det(\text{Menor}_{a_{3}})$$
en donde, el menor es el determinante de la matriz 2×2 que queda al eliminar a las filas y columnas de los elementos $latex a_{1}$, $latex a_{2}$ y $latex a_{3}$:
$$\det(\text{Menor}_{a_{1}}) = b_{2}c_{3} – b_{3}c_{2}$$
$$ \det(\text{Menor}_{a_{2}}) = b_{1}c_{3} – b_{3}c_{1}$$
$$\det(\text{Menor}_{a_{3}}) = b_{1}c_{2} – b_{2}c_{1}$$
Si es que usaramos la segunda fila, tendríamos los signos -, +, -:
$$\det(A) = – b_{1} \cdot \det(\text{Menor}_{b_{1}}) + b_{2} \cdot \det(\text{Menor}_{b_{2}}) – b_{3} \cdot \det(\text{Menor}_{b_{3}})$$
10 Ejercicios resueltos de determinante de matrices 3×3
EJERCICIO 1
Halla el determinante de la siguiente matriz de 3×3:
$$ B = \begin{bmatrix} 2 & 5 & 3 \\ 1 & 4 & 6 \\ 7 & 8 & 9 \ \end{bmatrix} $$
Solución
Para hallar el determinante de la matriz $latex B$, podemos utilizar el método de expansión cofactorial a lo largo de la primera fila.
Entonces, si es que denotamos al determinante por $latex |B|$ o $latex \det(B)$.
$latex |B| = 2 \cdot C_{11} – 5 \cdot C_{12} + 3 \cdot C_{13} $
En donde $latex C_{11}$, $latex C_{12}$, y $latex C_{13}$ son los cofactores de los elementos de la primera fila.
Para encontrar los cofactores, necesitamos calcular los determinantes de las matrices 2×2 obtenidas eliminando la fila y la columna de cada elemento de la primera fila:
$$ C_{11} = \begin{vmatrix} 4 & 6 \\ 8 & 9 \end{vmatrix} $$
$$= (4 \cdot 9) – (6 \cdot 8)$$
$$= 36 – 48 = -12$$
$$ C_{12} = \begin{vmatrix} 1 & 6 \\ 7 & 9 \end{vmatrix}$$
$$ = (1 \cdot 9) – (6 \cdot 7) $$
$$= 9 – 42 = -33 $$
$$ C_{13} = \begin{vmatrix} 1 & 4 \\ 7 & 8 \end{vmatrix} $$
$$= (1 \cdot 8) – (4 \cdot 7) $$
$$= 8 – 28 = -20$$
Ahora, sustituimos los valores de los cofactores en la fórmula del determinante:
$$ |B| = 2 \cdot (-12) – 5 \cdot (-33) + 3 \cdot (-20) $$
$$= -24 + 165 – 60 = 81 $$
Entonces, el determinante de la matriz 3×3 es 81.
EJERCICIO 2
Encuentra el determinante de la siguiente matriz:
$$B =\begin{bmatrix}1 & 4 & 7 \\2 & 5 & 8 \\3 & 6 & 9\end{bmatrix}$$
Solución
Podemos tomar la primera fila y formar la siguiente fórmula. Recuerda que multiplicamos a cada elemento por el determinante del menor correspondiente.
$$ |B| = b_{11}(b_{22}b_{33} – b_{23}b_{32}) – b_{12}(b_{21}b_{33} – b_{23}b_{31}) + b_{13}(b_{21}b_{32} – b_{22}b_{31}) $$
Sustituyendo los valores de la matriz B, tenemos:
$$ |B| = 1(5 \cdot 9 – 8 \cdot 6) – 4(2 \cdot 9 – 8 \cdot 3) + 7(2 \cdot 6 – 5 \cdot 3) $$
Simplificando, tenemos:
$$ |B| = 1(-3) – 4(-6) + 7(-3) $$
$$ |B| = -3 + 24 – 21 $$
$latex |B| = 0 $
EJERCICIO 3
Encuentra el determinante de la siguiente matriz:
$$ C = \begin{bmatrix} 3 & 0 & 2 \\ 4 & 1 & 5 \\ 7 & 8 & 9 \end{bmatrix} $$
Solución
Similar al ejercicio anterior, vamos a obtener una fórmula usando el método de expansión cofactorial en la primera fila:
$$|C| = c_{11}(c_{22}c_{33} – c_{23}c_{32}) – c_{12}(c_{21}c_{33} – c_{23}c_{31}) + c_{13}(c_{21}c_{32} – c_{22}c_{31})$$
Usando los valores de los elementos de la matriz C, tenemos:
$$|C| = 3(1 \cdot 9 – 5 \cdot 8) – 0(4 \cdot 9 – 5 \cdot 7) + 2(4 \cdot 8 – 1 \cdot 7)$$
Realizando las operaciones, tenemos:
$latex |C| = 3(-31) – 0(-1) + 2(25)$
$latex |C| = -93 + 0 + 50$
$latex |C| = -43$
EJERCICIO 4
¿Cuál es el determinante de la matriz D?
$$ D = \begin{bmatrix} -1 & 2 & -3 \\ 4 & -5 & 6 \\ -7 & 8 & -9 \end{bmatrix} $$
Solución
Usando la primera fila de la matriz, formamos la siguiente fórmula:
$$|D| = d_{11}(d_{22}d_{33} – d_{23}d_{32}) – d_{12}(d_{21}d_{33} – d_{23}d_{31}) + d_{13}(d_{21}d_{32} – d_{22}d_{31})$$
Sustituyendo los valores de los elementos de la matriz D en esta fórmula, tenemos:
$$|D| = -1(-5 \cdot -9 – 6 \cdot 8) – 2(4 \cdot -9 – 6 \cdot -7) + (-3)(4 \cdot 8 – (-5) \cdot -7)$$
Resolviendo las operaciones y simplificando, tenemos:
$$|D| = -1(45 – 48) – 2(-36 + 42) + (-3)(32 + 35)$$
$$|D| = -1(-3) – 2(-6) + (-3)(67)$$
$latex |D| = 3 + 12 – 201$
$latex |D| = -186$
EJERCICIO 5
Encuentra el determinante de la siguiente matriz:
$$ E = \begin{bmatrix} 2 & -4 & 6 \\ -1 & 3 & -7 \\ 4 & 5 & -6 \end{bmatrix} $$
Solución
Similar a los ejercicios anteriores, vamos a seleccionar la fila 1 para aplicar el método de cofactores:
$$|E| = e_{11}(e_{22}e_{33} – e_{23}e_{32}) – e_{12}(e_{21}e_{33} – e_{23}e_{31}) + e_{13}(e_{21}e_{32} – e_{22}e_{31})$$
Usando los valores de los elementos de la matriz E en la fórmula, tenemos:
$$|E| = 2(3 \cdot -6 – (-7) \cdot 5) – (-4)(-1 \cdot -6 – (-7) \cdot 4) + 6(-1 \cdot 5 – 3 \cdot 4)$$
Resolviendo las operaciones, tenemos:
$$|E| = 2(-18 + 35) – (-4)(6 + 28) + 6(-5 – 12)$$
$$|E| = 2(17) – (-4)(34) + 6(-17)$$
$$|E| = 34 + 136 – 102$$
$latex |E| = 68$
EJERCICIO 6
¿Cuál es el determinante de la matriz F?
$$ F = \begin{bmatrix} 3 & -2 & 1 \\ -1 & 4 & -5 \\ 2 & 6 & -3 \end{bmatrix} $$
Solución
Usando el método de expansión cofactorial, podemos formar la siguiente fórmula usando la primera fila de la matriz:
$$|F| = f_{11}(f_{22}f_{33} – f_{23}f_{32}) – f_{12}(f_{21}f_{33} – f_{23}f_{31}) + f_{13}(f_{21}f_{32} – f_{22}f_{31})$$
Usando los valores de los elementos de la matriz F, tenemos:
$$|F| = 3(4 \cdot -3 – (-5) \cdot 6) – (-2)(-1 \cdot -3 – (-5) \cdot 2) + 1(-1 \cdot 6 – 4 \cdot 2)$$
Resolviendo las operaciones, tenemos:
$$|F| = 3(-12 + 30) – (-2)(3 + 10) + 1(-6 – 8)$$
$$|F| = 3(18) – (-2)(13) + 1(-14)$$
$latex |F| = 54 + 26 – 14$
$latex |F| = 66$
EJERCICIO 7
Encuentra el determinante de la siguiente matriz:
$$ G = \begin{bmatrix} -4 & 7 & -1 \\ 5 & -2 & 6 \\ -3 & 1 & 8 \end{bmatrix} $$
Solución
Si es que tomamos la primera fila de la matriz, podemos formar la siguiente fórmula:
$$|G| = g_{11}(g_{22}g_{33} – g_{23}g_{32}) – g_{12}(g_{21}g_{33} – g_{23}g_{31}) + g_{13}(g_{21}g_{32} – g_{22}g_{31})$$
Usando esta fórmula con los valores de los elementos de la matriz G, tenemos:
$$|G| = -4(-2 \cdot 8 – 6 \cdot 1) – 7(5 \cdot 8 – 6 \cdot -3) + (-1)(5 \cdot 1 – (-2) \cdot -3)$$
Simplificando esta expresión, tenemos:
$$|G| = -4(-16 – 6) – 7(40 + 18) + (-1)(5 – 6)$$
$$|G| = -4(-22) – 7(58) + (-1)(-1)$$
$latex |G| = 88 – 406 + 1$
$latex |G| = -317$
EJERCICIO 8
¿Cuál es el determinante de la matriz H?
$$ H = \begin{bmatrix} 1 & 2 & 3 \\ -2 & 1 & -4 \\ 3 & -1 & 1 \end{bmatrix} $$
Solución
Al tomar la primera fila de la matriz, podemos multiplicar a cada elemento por el determinante del menor para formar la siguiente fórmula:
$$|H| = h_{11}(h_{22}h_{33} – h_{23}h_{32}) – h_{12}(h_{21}h_{33} – h_{23}h_{31}) + h_{13}(h_{21}h_{32} – h_{22}h_{31})$$
Sustituyendo los valores de los elementos de la matriz H, tenemos:
$$|H| = 1(1 \cdot 1 – (-4) \cdot (-1)) – 2(-2 \cdot 1 – (-4) \cdot 3) + 3(-2 \cdot (-1) – 1 \cdot 3)$$
Ahora, resolvemos las operaciones y simplificamos:
$$|H| = 1(1 – 4) – 2(-2 + 12) + 3(2 – 3)$$
$latex |H| = 1(-3) – 2(10) + 3(-1)$
$latex |H| = -3 – 20 – 3$
$latex |H| = -26$
EJERCICIO 9
Encuentra el determinante de la matriz I:
$$ I = \begin{bmatrix} 2 & 3 & -1 \\ -1 & 4 & 2 \\ 3 & -2 & 1 \end{bmatrix} $$
Solución
Formamos la siguiente fórmula al tomar la primera fila de la matriz I:
$$|I| = i_{11}(i_{22}i_{33} – i_{23}i_{32}) – i_{12}(i_{21}i_{33} – i_{23}i_{31}) + i_{13}(i_{21}i_{32} – i_{22}i_{31})$$
Sustituyendo los valores de la matriz I, tenemos:
$$|I| = 2(4 \cdot 1 – 2 \cdot -2) – 3(-1 \cdot 1 – 2 \cdot 3) + (-1)(-1 \cdot -2 – 4 \cdot 3)$$
Resolviendo las operaciones y simplificando:
$$|I| = 2(4 + 4) – 3(-1 – 6) + (-1)(2 – 12)$$
$latex |I| = 2(8) – 3(-7) + (-1)(-10)$
$latex |I| = 16 + 21 + 10$
$latex |I| = 47$
EJERCICIO 10
Encuentra el determinante de la matriz J:
$$ J = \begin{bmatrix} -1 & 3 & 5 \\ 3 & 2 & -1 \\ 1 & 1 & -2 \end{bmatrix} $$
Solución
Usando la primera fila de la matriz, formamos la siguiente fórmula:
$$|J| = j_{11}(j_{22}j_{33} – j_{23}j_{32}) – j_{12}(j_{21}j_{33} – j_{23}j_{31}) + j_{13}(j_{21}j_{32} – j_{22}j_{31})$$
Ahora, usamos los valores de los elementos de la matriz:
$$|J| = -1(2 \cdot -2 – (-1) \cdot 1) – 3(3 \cdot -2 – (-1) \cdot 1) + 5(3 \cdot 1 – 2 \cdot 1)$$
Resolviendo las operaciones, tenemos
$$|J| = -1(-4 – 1) – 3(-6 + 1) + 5(3 – 2)$$
$latex |J| = -1(-5) – 3(-5) + 5(1)$
$latex |J| = 5 + 15 + 5$
$latex |J| = 25$
Ejercicios de determinante de matrices 3×3 para resolver


Encuentra el determinante de $latex A=\begin{bmatrix} -8& 3& 5\\6& 7& -6\\-4& -5& 7\end{bmatrix}$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre matrices? Puedes mirar estas páginas:
–


