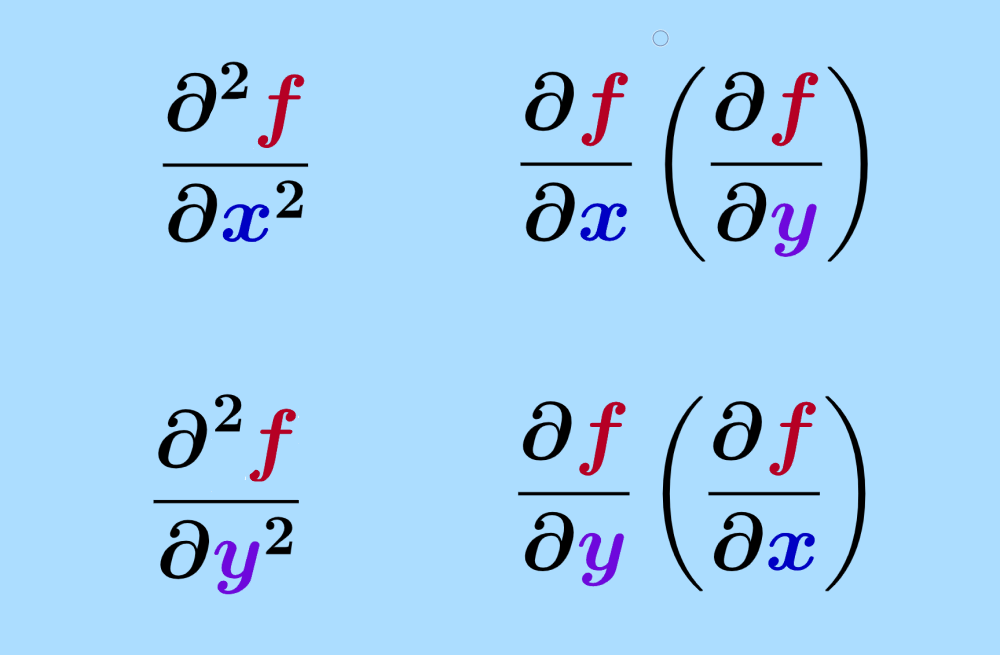Las derivadas parciales de segundo orden describen la razón a la que cambia la propia derivada parcial con respecto a sus variables. Esta información es fundamental para comprender sistemas complejos, desde el flujo de calor a través de una superficie hasta el comportamiento de los mercados económicos.
En este artículo exploraremos el concepto de derivadas parciales de segundo orden. Conoceremos cómo se calculan y veremos algunos ejercicios de práctica.
¿Cómo calcular derivadas parciales de segundo orden?
Las derivadas parciales de segundo orden son encontradas al calcular la derivada parcial de una función dos veces con respecto a las variables dadas.
Por ejemplo, si tenemos la función $latex z=f(x, y)$, entonces:
$latex \dfrac{\partial^2{f}}{\partial{x^2}}=\dfrac{\partial }{\partial{x}}\left(\dfrac{\partial f}{\partial x}\right)~$ y $latex \dfrac{\partial^2{f} }{\partial x^2}=\dfrac{\partial }{\partial{x}}\left(\dfrac{\partial f}{\partial x}\right)~$
Estas derivadas también pueden ser escritas como $latex f_{xx}$ y $latex f_{yy}$, que es la notación de subíndice.
Las derivadas parciales de segundo orden no tienen que ser necesariamente siempre con respecto a una misma variable. También podemos calcular derivadas parciales mixtas:
$latex \dfrac{\partial^2{f}}{\partial x\partial y}=\dfrac{\partial }{\partial{x}}\left(\dfrac{\partial f}{\partial y}\right)~$ y $latex \dfrac{\partial^2{f}}{\partial y \partial x}=\dfrac{\partial }{\partial{y}}\left(\dfrac{\partial f}{\partial x}\right)~$
Estas derivadas son denotadas como $latex f_{xy}$ y $latex f_{yx}$ respectivamente.
Nota: Como veremos en los ejercicios a continuación, resulta que $latex f_{xy}=f_{yx}$ siempre es verdadero.
Si necesitas hacer una revisión sobre las derivadas parciales de primer orden, puedes visitar este artículo.
Ejercicios resueltos de derivadas parciales de segundo orden
EJERCICIO 1
Encuentra la derivada $latex \dfrac{\partial^2{f} }{\partial x^2}$ de la siguiente función:
$$f(x, y) = 3x^2 + 4xy + y^2$$
Solución
Para calcular esta derivada, tenemos que derivar a la función dada dos veces con respecto a $latex x$, mientras la variable $latex y$ se mantiene constante.
Entonces, la derivada parcial de primer orden con respecto a $latex x$ es:
$$\dfrac{\partial{d}f}{\partial x}=6x+4y$$
Al derivar al término $latex 3x^2$ con respecto a $latex x$, tenemos $latex 6x$. Al derivar al término $latex 4xy$ con respecto a $latex x$, tenemos $latex 4y$.
La derivada de $latex y^2$ con respecto a $latex x$ es cero, ya que la variable $latex y$ se mantiene constante.
Ahora, derivamos a $latex \dfrac{\partial f}{\partial x}$ con respecto a $latex x$:
$$\dfrac{\partial^2{f}}{\partial x^2}=6$$
EJERCICIO 2
¿Cuál es la derivada $latex \dfrac{\partial^2{f}}{\partial y^2}$ de la siguiente función?
$$f(x, y) = 3x^2 + 4xy + y^2$$
Solución
En este caso, vamos que derivar a la función dada dos veces con respecto a $latex y$, mientras la variable $latex x$ se mantiene constante.
Entonces, derivando a la función con respecto a $latex y$, tenemos:
$$\dfrac{\partial f}{\partial y}=4x+2y$$
El término $latex 3x^2$ es constante, por lo que su derivada es cero.
Ahora, podemos calcular la $latex \dfrac{\partial f}{\partial y}$ con respecto a $latex y$:
$$\dfrac{\partial^2{f} }{\partial y^2}=2$$
EJERCICIO 3
Encuentra las derivadas $latex f_{xy}$ y $latex f_{yx}$ de la siguiente función:
$$f(x, y) = 3x^2 + 4xy + y^2$$
Solución
Para resolver este ejercicio, tenemos que calcular las derivadas parciales de la función tanto con respecto a $latex x$, como con respecto a $latex y$:
$latex f_{x}=6x+4y$
$latex f_{y}=4x+2y$
Ahora, encontramos la derivada de segundo orden de $latex f_{x}$ y $latex f_{y}$ con respecto a la otra variable:
$latex f_{xy}=4$
$latex f_{yx}=4$
Vemos que la derivada obtenida es la misma. La igualdad $latex f_{xy}=f_{yx}$ siempre es verdadera.
EJERCICIO 4
Halla las derivadas parciales de segundo orden de
$latex f(x, y) = x^3y + x^2y^2$
Solución
Para empezar, hallamos las derivadas parciales de primer orden:
$$f_{x} = 3x^2y + 2xy^2$$
$$f_{y} = x^3 + 2xy$$
A continuación, diferenciamos cada una de estas derivadas parciales de primer orden con respecto a la misma variable y a la otra variable:
$latex f_{xx} = 6xy + 6x^2$
$latex f_{xy} = 3x^2 + 4xy$
$latex f_{yx} = 3x^2 + 4xy$
$latex f_{yy} = 2x$
EJERCICIO 5
Encuentra las cuatro derivadas parciales de segundo orden de
$latex f(x, y)=x^2+xy^3-y^2$
Solución
Para encontrar las cuatro derivadas parciales de segundo orden, tenemos que empezar calculando las dos derivadas parciales de primer orden:
$latex f_{x}=2x+y^3$
$latex f_{y}=3xy^2-2y$
Ahora, podemos derivar cada una de estas expresiones con respecto a $latex x$ y a $latex y$:
$latex f_{xx}=2$
$latex f_{xy}=3y^2$
$latex f_{yx}=3y^2$
$latex f_{yy}=6xy-2$
EJERCICIO 6
Encuentra las derivadas parciales de segundo orden de la siguiente función:
$latex f(x, y) = x^3y^2 – 2x^2y + 5xy^3$
Solución
Primero, hallamos las derivadas parciales de primer orden con respecto a $latex x$ y con respecto a $latex y$:
$latex f_{x} = 3x^2y^2 – 4xy + 5y^3$
$latex f_{y} = 2x^3y – 2x^2 + 15xy^2$
A continuación, diferenciamos cada una de estas derivadas parciales de primer orden con respecto a ambas variables:
$latex f_{xx} = 6xy^2 – 4$
$latex f_{xy} = 6x^2y-4x + 15y^2$
$latex f_{yx} = 6x^2y-4x+15y^2$
$latex f_{yy} = 2x^3 + 30xy$
EJERCICIO 7
Tenemos la función $latex f(x, y)= ax^2+by^2$, en donde $latex a $ y $latex b$ son constantes.
Encuentra la relación entre $latex a$ y $latex b$ de modo que $latex f_{xx}+f_{yy}=0$.
Solución
Para resolver este problema, empezamos encontrando las derivadas parciales de primer orden:
$latex f_{x}=2ax$
$latex f_{y}=2by$
Ahora, podemos calcular las derivadas parciales $latex f_{xx}$ y $latex f_{yy}$:
$latex f_{xx}=2a$
$latex f_{yy}=2b$
Esto significa que tenemos:
$latex f_{xx}+f_{yy}=2a+2b$
Queremos que esto sea igual a 0, por lo que tenemos $latex b=-a$. Por lo tanto, la función original puede escribirse como:
$latex f(x,y)=a(x^2-y^2)$
EJERCICIO 8
Encuentra las cuatro derivadas parciales de segundo orden de la siguiente función:
$latex f(x, y) = \sin(x)\cos(y)$
Solución
Las derivadas parciales de primer orden son:
$latex f_{x} = \cos(x)\cos(y)$
$latex f_{y} = -\sin(x)\sin(y)$
Luego, derivamos a cada una de esas derivadas parciales de primer orden con respecto a ambas variables:
$latex f_{xx} = -\sin(x)\cos(y)$
$latex f_{xy} = -\cos(x)\sin(y)$
$latex f_{yx} = -\cos(x)\sin(y)$
$latex f_{yy} = -\sin(x)\cos(y)$
Ejercicios de derivadas parciales de segundo grado para resolver
Encuentra la derivada parcial $latex f_{xy}$ de $latex f(x, y) = x^2\sin(y)+\cos(2x)y$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre derivadas parciales? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
