Las ecuaciones del movimiento o cinemáticas ilustran la relación entre desplazamiento, velocidad, aceleración y tiempo en condiciones de aceleración constante. Sirven de base para comprender el movimiento de los objetos en diversas situaciones, desde una manzana que cae de un árbol hasta un cohete que viaja al espacio.
En este artículo exploraremos en detalle las ecuaciones del movimiento rectilíneo uniformemente acelerado. Comprenderlas es una poderosa herramienta para entender la dinámica del mundo que nos rodea.
FÍSICA
Relevante para…
Aprender sobre las ecuaciones cinemáticas para una aceleración constante.
FÍSICA
Relevante para…
Aprender sobre las ecuaciones cinemáticas para una aceleración constante.
Las cinco ecuaciones fundamentales del movimiento rectilíneo uniformemente acelerado
Las ecuaciones cinemáticas son un conjunto de ecuaciones que nos permiten calcular las distintas magnitudes que intervienen cuando un objeto se mueve con una aceleración constante. Las magnitudes que nos interesan son
- $latex s=$ desplazamiento
- $latex u=$ velocidad inicial
- $latex v=$ velocidad final
- $latex a=$ aceleración
- $latex t=$ tiempo
Estas son las cinco ecuaciones fundamentales del movimiento rectilíneo uniformemente acelerado:
Ecuación 1: $latex v=u+at$
Ecuación 2: $latex s=\dfrac{u+v}{2}\times t$
Ecuación 3: $latex s=ut+\frac{1}{2}at^2$
Ecuación 4: $latex s=vt-\frac{1}{2}at^2$
Ecuación 5: $latex v^2=u^2+2as$
Las siguientes son las explicaciones de las ecuaciones y sus componentes.
- $latex v = u + at$: Esta ecuación expresa que el cambio de velocidad es igual a la aceleración multiplicada por el intervalo de tiempo.
- $latex s=\frac{u+v}{2}\times t$: Esta ecuación presenta el desplazamiento como el producto de la velocidad media (la suma de las velocidades inicial y final dividida por 2) y el tiempo.
- $latex s=ut+\frac{1}{2}at^2$: Esto significa que el desplazamiento de un objeto es el producto de la velocidad inicial y el tiempo más la mitad de la aceleración por el cuadrado del tiempo.
- $latex s=vt-\frac{1}{2}at^2$: Esta es una versión reordenada de la tercera ecuación, que es útil cuando la velocidad inicial no se da o no se considera.
- $latex v^2=u^2+2as$: Esto significa que el cuadrado de la velocidad final es igual al cuadrado de la velocidad inicial más el doble de la aceleración por el desplazamiento.
Nota: Cada ecuación se utiliza en circunstancias específicas y contiene información particular sobre el movimiento del objeto. Saber qué ecuación usar en diferentes escenarios es crucial para resolver problemas de movimiento rectilíneo uniforme con precisión.
¿CómoeElegir la ecuación de MRUV correcta?
La elección de la ecuación adecuada depende en gran medida de las variables indicadas en cada problema. Por lo tanto, hay que empezar escribiendo las cantidades que conocemos y la cantidad que queremos hallar.
La siguiente tabla puede servir de guía para determinar la ecuación correcta que debe utilizar.
| Problema | Ecuación | Empieza de reposo |
|---|---|---|
| Se pide velocidad y se dan $latex a$, $latex t$ | $latex v=u+at$ | $latex v=at$ |
| Se pide desplazamiento y se dan $latex u$, $latex v$, $latex t$ | $latex s=\dfrac{u+v}{2}\times t$ | – |
| Se pide desplazamiento y se dan $latex u,~ a$, $latex t$ | $latex s=ut+\frac{1}{2}at^2$ | $latex s=\frac{1}{2}at^2$ |
| Se pide desplazamiento y se dan $latex v,~a$, $latex t$ | $latex s=vt-\frac{1}{2}at^2$ | $latex s=vt-\frac{1}{2}at^2$ |
| El tiempo no se da ni se pide | $latex v^2=u^2+2as$ | $latex v=\sqrt{2as}$ |
| La velocidad es constante ($latex a=0$) | $latex v=\dfrac{s}{t}~$ o $latex ~s=vt$ | – |
Nota: Esta tabla muestra las formas simplificadas de estas ecuaciones aplicables cuando se trata de objetos que parten del reposo, velocidad inicial igual a 0 o $latex u=0$.
Proceso de resolución de problemas con las ecuaciones en MRUV
La mayoría de los problemas relacionados con las ecuaciones cinemáticas pueden resolverse mediante el siguiente procedimiento:
Paso 1: Crear una lista con las cantidades que conocemos y las que queremos encontrar.
Paso 2: Elige la ecuación que relaciona estas cantidades. La tabla anterior puede servirte de guía.
Paso 3: Sustituye los valores conocidos y resuelve las incógnitas.
Demostraciones de las ecuaciones de movimiento rectilíneo uniformemente acelerado
Las ecuaciones del movimiento rectilíneo uniformemente acelerado se derivan de las definiciones de velocidad y aceleración.
Podemos usar la siguiente gráfica de velocidad vs tiempo para ayudarnos a encontrar las ecuaciones. La gráfica representa el movimiento de un objeto con velocidad inicial $latex u$. Después de un tiempo $latex t$, su velocidad final es $latex v$.
Ecuación 1
La gráfica mostrada anteriormente muestra una línea recta, lo que significa que la aceleración $latex a$ es constante. La pendiente de la recta de un gráfico de velocidad vs tiempo es igual a la aceleración.
La aceleración o pendiente de la recta se define como:
$$ a=\frac{v-u}{t}$$
Resolviendo para $latex v$ nos da la primera ecuación de movimiento:
$latex v=u+at$
Ecuación 2
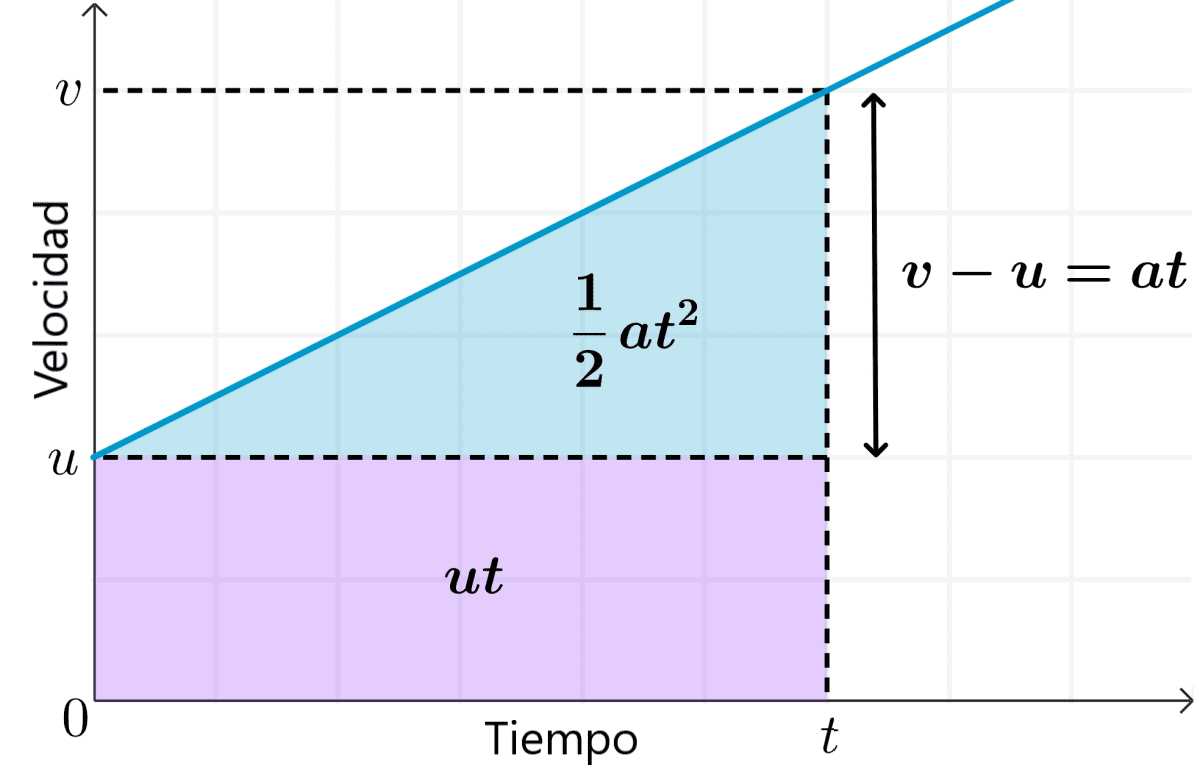
En un gráfico velocidad vs tiempo, el área bajo el gráfico representa el desplazamiento. Entonces, el desplazamiento del objeto es el área sombreada en la siguiente figura:
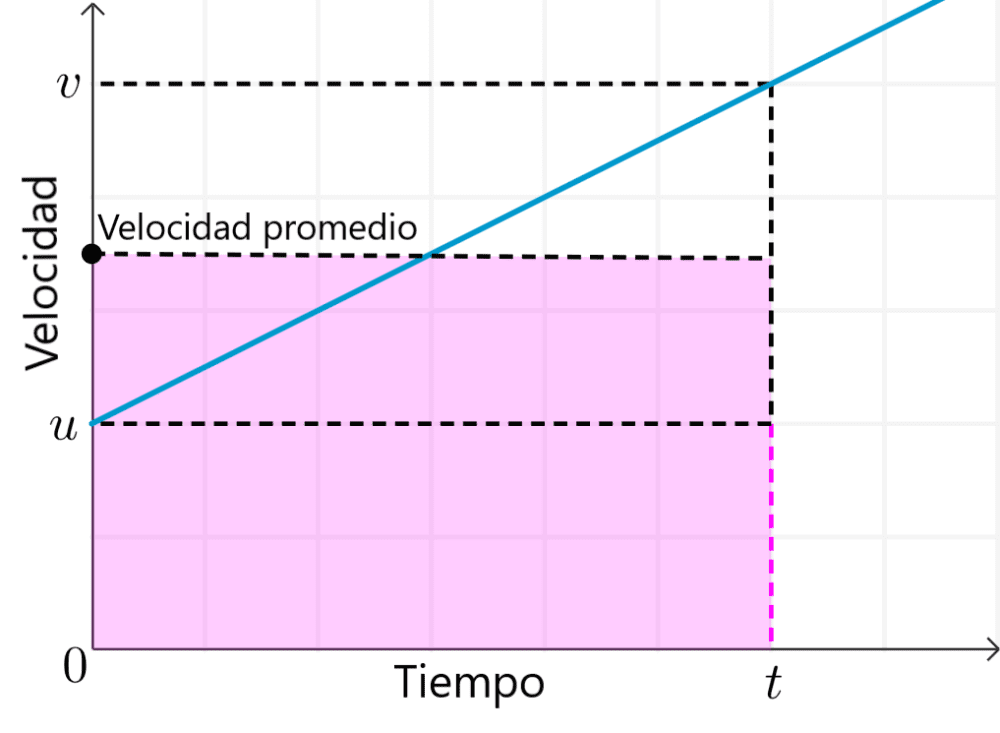
Dado que las velocidades inicial y final son diferentes, calculamos el desplazamiento utilizando la velocidad promedio, que viene dada por:
$$\frac{u+v}{2}$$
Como la zona sombreada de la figura anterior es un rectángulo, solo tenemos que multiplicar la velocidad promedio por el tiempo empleado:
$$s=\frac{(u+v)}{2}\times t$$
Ecuación 3
Podemos derivar la ecuación 3 utilizando las ecuaciones 1 y 2.
$latex \text{(1)}~~v=u+at$
$latex \text{(2)}~~s=\dfrac{(u+v)}{2}\times t$
Sustituyendo $latex v$ de la ecuación 1 en la ecuación 2, obtenemos:
$$s=\frac{(u+u+at)}{2}\times t$$
$$s=\frac{(2u+at)}{2}\times t$$
$$s=\frac{2ut}{2}+\frac{at^2}{2}$$
$$s=ut+\frac{at^2}{2}$$
Esto también puede verse en la figura anterior, donde los términos $latex ut$ y $latex at^2$ son las áreas bajo la gráfica que representan el desplazamiento.
Ecuación 4
Similar a la ecuación 3, solo usamos las ecuaciones 1 y 2.
$latex \text{(1)}~~v=u+at$
$latex \text{(2)}~~s=\dfrac{(u+v)}{2}\times t$
Sin embargo, aquí sustituimos $latex u=v-at$ de la ecuación 1 en la ecuación 2 para obtener:
$$s=\frac{(v+v-at)}{2}\times t$$
$$s=\frac{(2v-at)}{2}\times t$$
$$s=\frac{2vt}{2}-\frac{at^2}{2}$$
$$s=vt-\frac{at^2}{2}$$
Ecuación 5
De nuevo, utilizamos las ecuaciones 1 y 2:
$latex \text{(1)}~~v=u+at$
$latex \text{(2)}~~s=\dfrac{(u+v)}{2}\times t$
Sustituimos $latex t=\frac{v-u}{a}$ de la ecuación 1 en la ecuación 2 para obtener:
$$s=\frac{(u+v)}{2}\times \frac{(v-u)}{a}$$
$$2as=(u+v)(v-u)$$
$$2as=v^2-u^2$$
$$v^2=u^2+2as$$
Aplicaciones prácticas de las ecuaciones cinemáticas
Ejemplos de la vida cotidiana
Los principios en los que se basan las ecuaciones cinemáticas están presentes en nuestra vida cotidiana. Por ejemplo, cuando conduces, la distancia que recorres en el tiempo y la velocidad que alcanzas pueden calcularse mediante ecuaciones cinemáticas.
Del mismo modo, si lanzas una pelota hacia arriba, puedes calcular la altura máxima que alcanzará y cuánto tardará en llegar de nuevo al suelo, suponiendo una aceleración constante debida a la gravedad.
Ingeniería y aplicaciones tecnológicas
En ingeniería y tecnología, las ecuaciones cinemáticas se utilizan en todas partes. Por ejemplo, los ingenieros mecánicos utilizan estas ecuaciones para diseñar vehículos y maquinaria. En el campo de la robótica, las ecuaciones se utilizan para programar robots que se muevan con precisión.
Estas ecuaciones se utilizan incluso en informática y desempeñan un papel crucial en el desarrollo de videojuegos, sobre todo para crear movimientos y físicas más realistas en el mundo virtual.
Experimentos científicos
Las ecuaciones cinemáticas son indispensables en diversos experimentos científicos. Los físicos utilizan a menudo estas ecuaciones para diseñar e interpretar experimentos que implican movimiento. Por ejemplo, en física de partículas, los investigadores que estudian el comportamiento de partículas sometidas a diversas fuerzas suelen utilizar ecuaciones cinemáticas para comprender el movimiento de las partículas.
Viajes espaciales y ciencia espacial
Quizá una de las aplicaciones más fascinantes de las ecuaciones cinemáticas sea la de los viajes espaciales y los cohetes. Al lanzar un cohete o un satélite, los científicos e ingenieros deben calcular la trayectoria y la velocidad necesarias para escapar de la atracción gravitatoria de la Tierra y llegar a un destino concreto.
Al aterrizar una nave espacial, deben calcular la deceleración necesaria para garantizar un aterrizaje seguro. En todos estos cálculos intervienen las ecuaciones cinemáticas, lo que demuestra perfectamente su importancia.
A partir de estos ejemplos, queda claro que las ecuaciones cinemáticas no son solo conceptos teóricos, sino que tienen aplicaciones en el mundo real.
Veáse también
¿Quieres saber más sobre velocidad y aceleración? Puede visitar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
