Una integral doble es un concepto matemático que permite hallar el volumen o el área de un objeto o región tridimensional en el plano. Las integrales dobles pueden expresarse en coordenadas rectangulares o polares y pueden evaluarse utilizando diversas técnicas.
En este artículo, daremos una visión general de las integrales dobles y demostraremos cómo evaluarlas utilizando ejercicios. Además, veremos algunos ejercicios de práctica.
¿Cómo resolver integrales dobles?
Para hallar una integral doble, primero hay que identificar una región en el plano sobre la que se quiere integrar. Esta región puede definirse mediante inecuaciones o dibujando una curva límite.
Recordemos que la integral de una función representa el área bajo la curva. En el caso de integrales dobles, la integral es el volumen bajo una superficie:
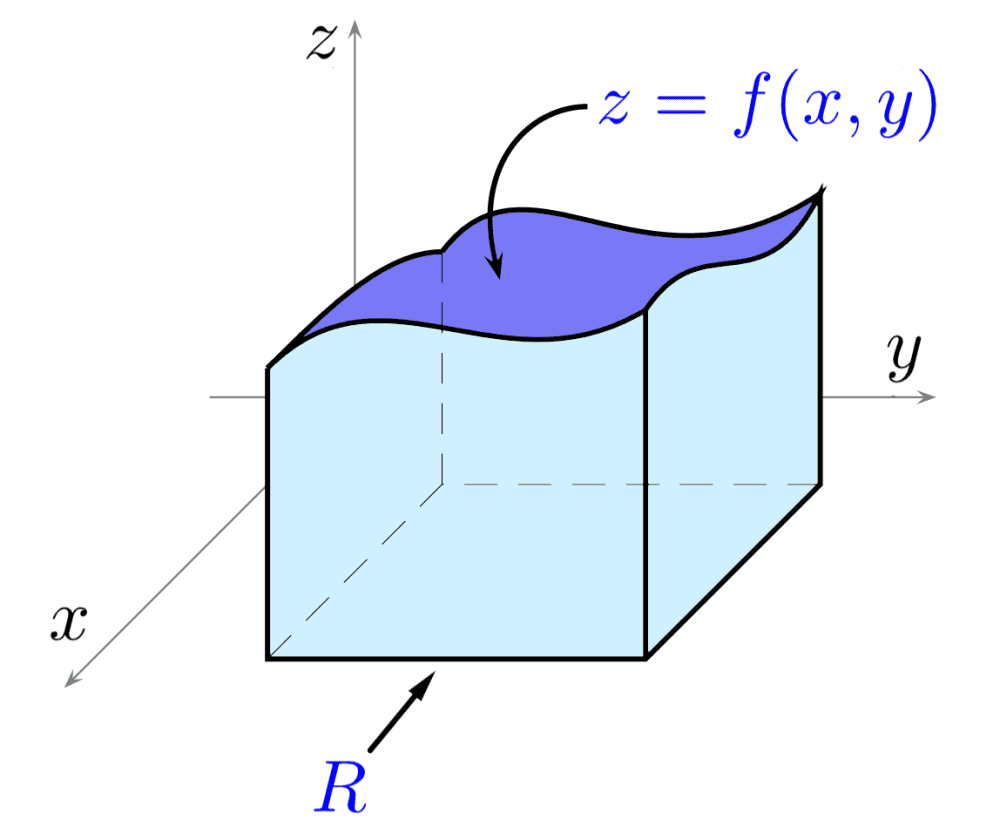
$$\int \int_{R} f(x, y)dA$$
Aquí, R es la región sobre la cual integramos y $latex dA $ es el elemento de área, una versión infinitesimal de $latex \delta A$.
$latex dA$ depende de las coordenadas. En coordenadas cartesinas, tenemos:
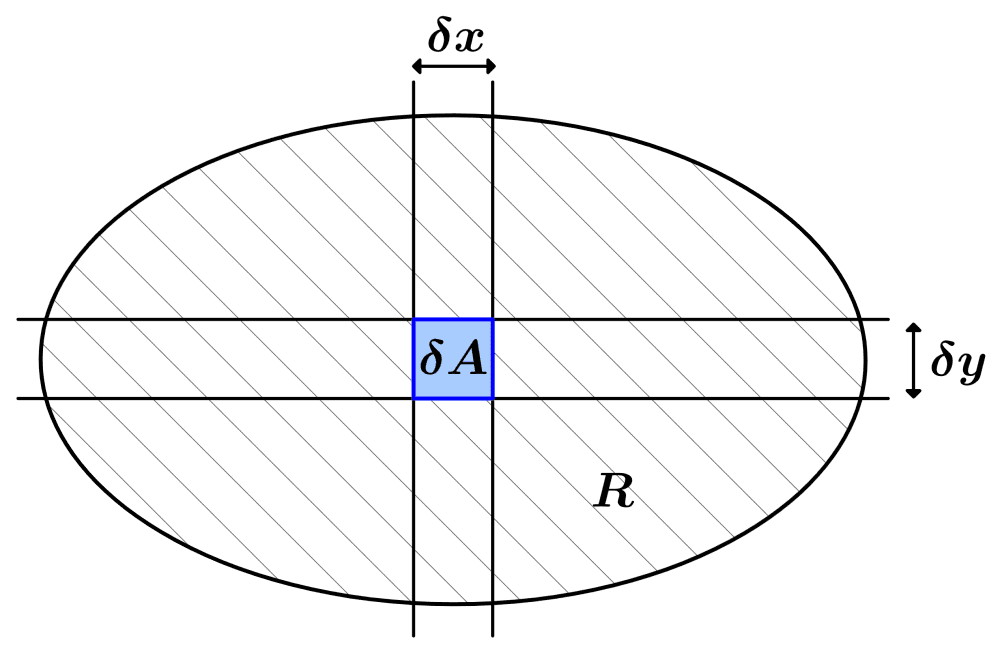
Claramente, vemos que $latex \delta A=\delta x \delta y$, por lo que tenemos $latex dA=dxdy$.
Entonces, esta integral se evalúa como:
$$\int \int_{R} f(x, y)dA= \int \int_{R} f(x, y)dxdy$$
Ahora, supongamos que la región de integración R es un rectángulo definido por $latex a\leq x \leq b$ y $latex c\leq y \leq d$. Entonces, la integral es:
$$\int \int_{R} f(x, y)dxdy= \int_{y=c}^{d} \left(\int_{x=a}^{b} f(x, y)dx \right)dy$$
Primero, evaluamos la integral interna y luego la externa. En este caso, la integral interna es con respecto a $latex x$.
Sin embargo, el orden no importa, ya que podríamos evaluar la integral con respecto a $latex y$ primero.
Ejercicios resueltos de integrales dobles
EJERCICIO 1
En la siguiente integral doble, indicar la región $latex R$ de integración y hallar su valor:
$$\int_{0}^{2} \int_{0}^{1}(1+2x+2y)dy dx$$
Solución
La región de integración es un rectángulo de vértices: $latex (0,0)$, $latex (2,0)$, $latex (0,1)$ y $latex (2,1)$.
Ahora bien, para resolver la integral, se comienza por la más interna, que en este caso, es la que corresponde a la variable $latex y$:
$$\int_{0}^{2} \int_{0}^{1}(1+2x+2y)dy dx=\int_{0}^{2}\left[ \int_{0}^{1}(1+2x+2y)dy \right]dx$$
Por lo tanto, se calcula la siguiente integral simple respecto a $latex y$, tratando a la variable $latex x$ como si fuera constante:
$$\int_{0}^{1}(1+2x+2y)dy=\int_{0}^{1}dy+2x\int_{0}^{1}dy+2\int_{0}^{1}ydy$$
$$=y\Big|_{0}^{1}+2xy\Big|_{0}^{1}+y^2\Big|_{0}^{1}$$
$$=(1-0)+2x(1-0)+(1^2-0^2)$$
$$=1+2x+1=2+2x$$
El resultado obtenido se sustituye entre los corchetes de la integral planteada al comienzo:
$$\int_{0}^{2}\left[ \int_{0}^{1}(1+2x+2y)dy \right]dx=\int_{0}^{2}(2+2x)dx$$
Y se resuelve la integral resultante respecto a la variable $latex x$:
$$\int_{0}^{2}(2+2x)dx=2\int_{0}^{2}dx+2\int_{0}^{2}xdx$$
$$2x\Big|_{0}^{2}+x^2\Big|_{0}^{2}=2(2-0)+(2^2-0^2)$$
$$=4+4=8$$
EJERCICIO 2
Calcular la integral doble:
$$\iint(1+6xy^2)dxdy$$
Sobre la región plana que consiste en el rectángulo dado por: $latex R=[0,2] \times [-1,1]$
Solución
Se debe calcular la integral sobre los límites dados por $latex R$, eligiendo un determinado orden (teorema de Fubini), ya que la función es continua en la región de integración.
Puesto que la región dada es un rectángulo, la variable $latex x$ va desde $latex 0$ hasta $latex 2$, mientras que la variable $latex y$ lo hace desde $latex -1$ hasta $latex 1$.
Comenzando a integrar la variable $latex y$, se tiene:
$$\int_{0}^{2}\left [ \int_{-1}^{1}(1+6xy^{2})dy \right ]dx$$
En primer lugar, se resuelve la integral entre corchetes, donde la variable de integración es $latex y$, mientras que $latex x$ se mantiene constante:
$$\int_{-1}^{1}(1+6xy^{2})dy =\int_{-1}^{1}dy+6x\int_{-1}^{1} y^{2}dy $$
$$=y\Big|_{-1}^{1}+6x\left(\dfrac{y^3}{3}\right)\Big|_{-1}^{1}$$
$$=[1-(-1)]+6x\left[\dfrac{1^3}{3}-\dfrac{(-1)^3}{3}\right]$$
$$=2+4x$$
Ahora se sustituye este resultado en lugar de los corchetes de la integral dada al comienzo, y se integra respecto a la variable $latex x$:
$$\int_{0}^{2}\left [ \int_{-1}^{1}(1+6xy^{2})dy \right ]dx=\int_{0}^{2}(2+4x)dx$$
$$=\int_{0}^{2}2dx+\int_{0}^{2}4xdx$$
$$=2x\Big|_{0}^{2}+4\left(\dfrac{x^2}{2}\right)\Big|_{0}^{2}$$
$$=2(2-0)+4\left(\dfrac{2^2}{2}-\dfrac{0^2}{2}\right)$$
$$=4+8=12$$
EJERCICIO 3
Calcular la siguiente integral doble:
$$\int_0^3\int_{4x/3}^{\sqrt{25-x^2}}xdydx$$
Solución
El recinto de integración es la región comprendida entre la recta $latex y=\dfrac{4x}{3}$ y la circunferencia $latex x^2+y^2=25$, como se muestra en la figura:
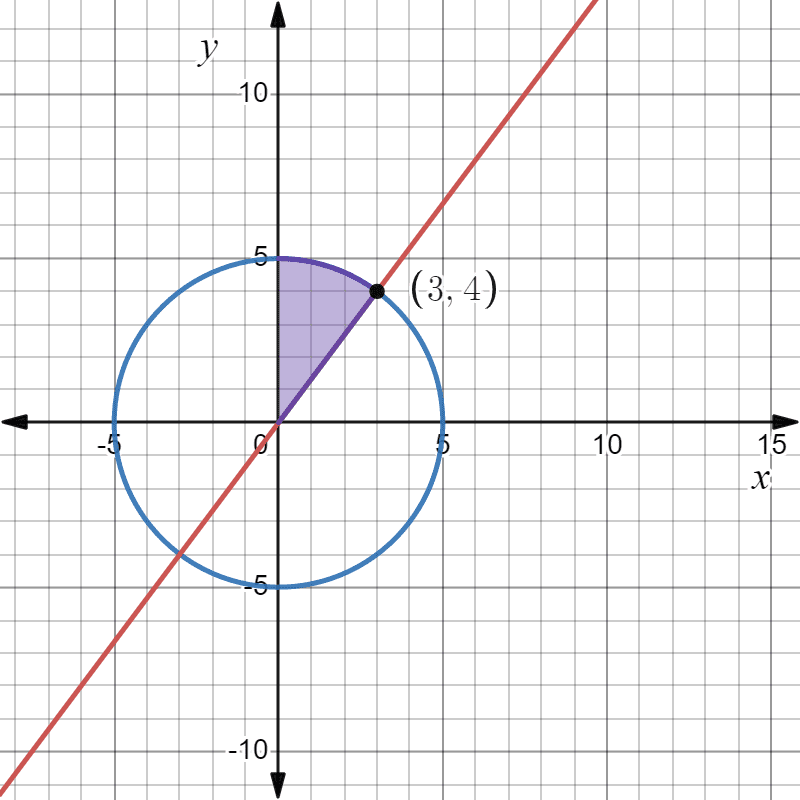
En dicha región, la intersección entre ambas curvas es el punto $latex P(3,4)$ y tal como está planteada la integral, primero se integra respecto a la variable $latex y$, que va desde la recta $latex y =\dfrac{4x}{3}$ hasta la circunferencia $latex +\sqrt{25-x^2}$, permaneciendo constante la variable $latex x$:
$$\int_0^3\int_{4x/3}^{\sqrt{25-x^2}}xdydx=\int_0^3x\left[\int_{4x/3}^{\sqrt{25-x^2}}dy\right]dx$$
La integral entre corchetes es:
$$\int_{4x/3}^{\sqrt{25-x^2}}dy=\int_{4x/3}^{\sqrt{25-x^2}}dy=$$
$$=y\Big|_{4x/3}^{\sqrt{25-x^2}}=\sqrt{25-x^2}-\dfrac{4x}{3}$$
Enseguida se sustituye este resultado en la integral original:
$$\int_0^3x\left[\int_{4x/3}^{\sqrt{25-x^2}}dy\right]dx=\int_0^3x\left[\sqrt{25-x^2}-\dfrac{4x}{3}\right]dx$$
$$=\int_0^3x\sqrt{25-x^2}dx-\int_0^3\dfrac{4x^2}{3}dx= I_1-I_2$$
Cálculo de $latex I_1$
La integral $latex I_1$ se resuelve mediante un cambio de variable:
- $latex u = 25-x^2$
- $latex du =-2xdx$
$$I_1 =\displaystyle\int_0^3x\sqrt{25-x^2}dx$$
$$=-\dfrac{1}{2}\displaystyle\int_{25}^{16} \sqrt{u}du$$
$$=\left(-\dfrac{1}{2}\right)\dfrac{u^\frac{3}{2}}{\frac{3}{2}}\Big|_{25}^{16}$$
$$=-\left(\dfrac{1}{3}\right){u^\frac{3}{2}}\Big|_{25}^{16}$$
$$=-\left(\dfrac{1}{3}\right)\left(\sqrt{16^3}-\sqrt{25^3}\right)=\dfrac{61}{3}$$
Cálculo de $latex I_2$
$$\displaystyle \int_0^3\dfrac{4x^2}{3}dx= \left(\dfrac{4}{3}\right)\dfrac {x^3}{3}\Big|_0^3=12$$
Por lo tanto:
$$\int_0^3\int_{4x/3}^{\sqrt{25-x^2}}xdydx=\dfrac{61}{3}-12=\dfrac{25}{3}$$
EJERCICIO 4
En la integral del ejercicio 3, intercambiar el orden de integración y plantear la integral resultante.
Solución
En este caso, la región de integración quedaría dividida en dos partes, la primera es un triángulo cuyos vértices son $latex (0,0)$, $latex (0,4)$ y $latex (3,4)$, mientras que la segunda es el sector por encima del segmento negro, el eje y y la circunferencia, según se advierte en la gráfica:
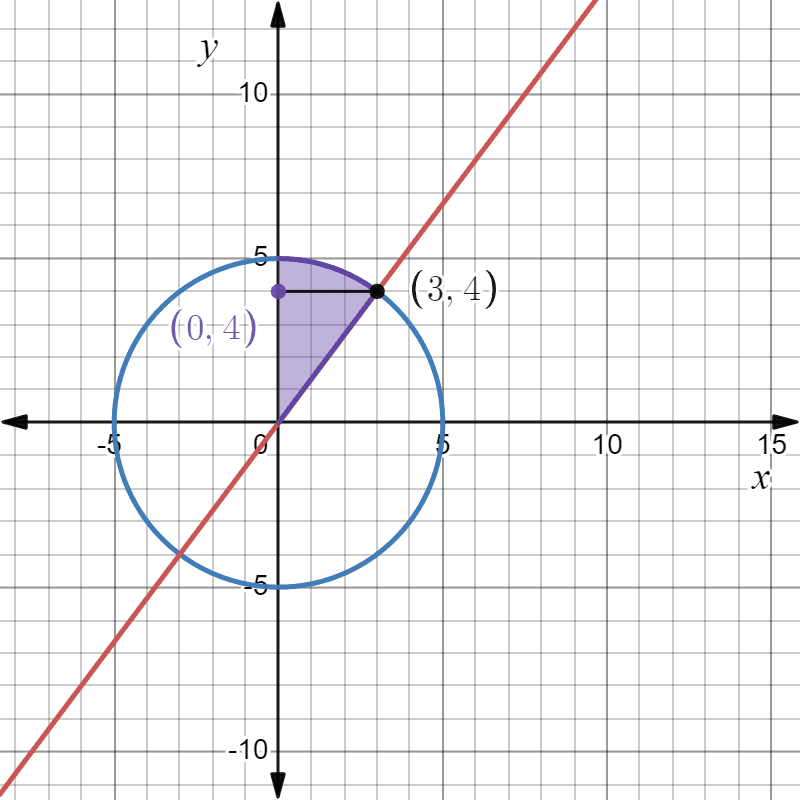
Por lo tanto, es preciso plantear una integral para cada región y luego sumar los respectivos resultados.
Primero se integraría sobre la variable $latex x$, la cual va desde $latex x=0$ hasta la recta $latex x =\dfrac{3y}{4}$, mientras que la variable $latex y$ iría desde $latex y=0$ hasta $latex y=4$.
Luego hay que añadir la región que va desde $latex x = 0$ hasta la circunferencia $latex x=\sqrt {25-y^2}$, en la cual $latex y$ varía desde $latex y=4$ hasta $latex y=5$:
$$\int_0^3\int_{4x/3}^{\sqrt{25-x^2}}xdydx=\int_0^4\left[\int_{0}^{\frac{3y}{4}}xdx\right]dy+\int_4^5\left[\int_{0}^{\sqrt {25-y^2}}xdx\right]dy$$
EJERCICIO 5
Resolver las integrales planteadas en el ejercicio 4 y comparar con el resultado obtenido en el ejercicio 3.
Solución
$$\int_0^3\int_{4x/3}^{\sqrt{25-x^2}}xdydx=\int_0^4\left[\int_{0}^{\frac{3y}{4}}xdx\right]dy+\int_4^5\left[\int_{0}^{\sqrt {25-y^2}}xdx\right]dy=$$
$$=I_1+I_2$$
Cálculo de $latex I_1$
$$\displaystyle \int_0^4\left[\int_{0}^{\frac{3y}{4}}xdx\right]dy=\int_0^4\left[\dfrac{x^2}{2}\right]_0^{\frac{3y}{4}}dy$$
$$=\displaystyle\int_0^4\dfrac{9y^2}{32}dy=\left(\dfrac{3}{32}\right)y^3\Big|_0^4=6$$
Cálculo de $latex I_2$
$$\displaystyle\int_4^5\left[\int_{0}^{\sqrt {25-y^2}}xdx\right]dy=\int_4^5\dfrac{x^2}{2}\Big|_0^{\sqrt {25-y^2}}dy$$
$$=\dfrac{1}{2}\int_4^5 (25-y^2)dy=$$
$$=\dfrac{1}{2}\left[25y\Big|_4^5-\dfrac{y^3}{3}\Big|_4^5\right]$$
$$=\dfrac{1}{2}\left(25-\dfrac{61}{3}\right)=\dfrac{7}{3}$$
Por lo tanto:
$$\int_0^3\int_{4x/3}^{\sqrt{25-x^2}}xdydx=6+\dfrac{7}{3}=\dfrac{25}{3}$$
Este resultado es el mismo que el obtenido en el ejercicio 3, como era de esperar.
EJERCICIO 6
Calcular:
$$\int\int_R xdA$$
Donde $latex R$ es la región comprendida entre $latex y=2x$ y $latex y=x^2$
Solución
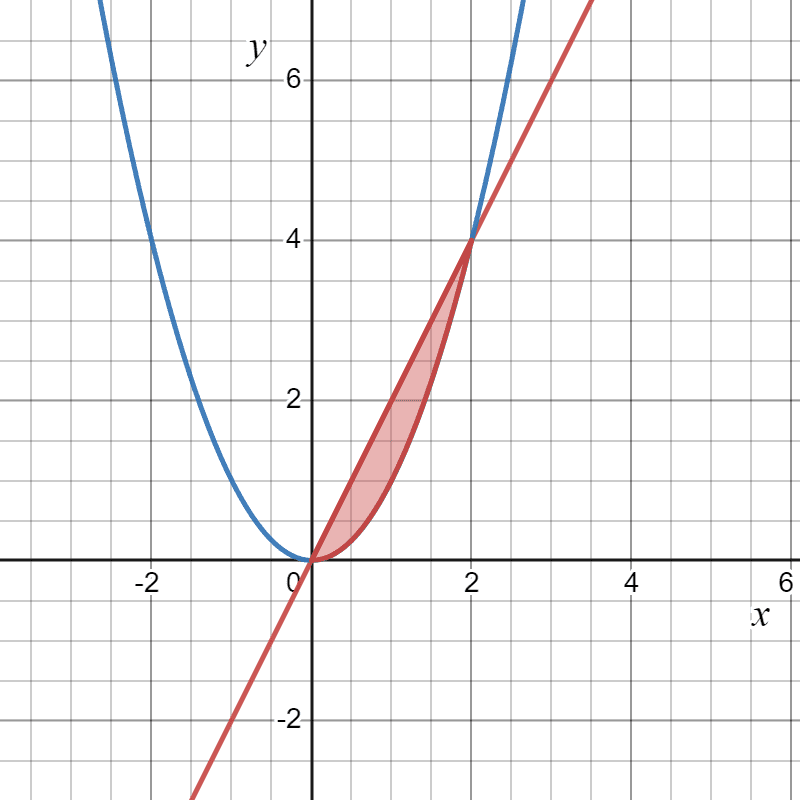
Para resolver la integral propuesta es necesario identificar $latex R$, la cual se muestra en la figura de la izquierda.
Se trata de la región sombreada, comprendida entre la recta $latex y=2x$ y la parábola $latex y=x^2$.
Una forma de calcular la integral es llevando a cabo un barrido vertical. De esta forma, la función varía desde la parábola $latex y=x^2$ hasta la recta $latex y=2x$, mientras que la variable $latex x$ lo hace desde $latex x=0$ hasta $latex x=2$.
En tal caso:
$$\int\int_R xdA=\int_0^2 x\left[\int_{x^2}^{2x}dy\right]dx$$
Enseguida se procede a resolver la integral entre corchetes:
$$\int_{x^2}^{2x}dy=y\Big|_{x^2}^{2x}=2x-x^2$$
Luego se sustituye el resultado y se integra respecto a $latex x$:
$$\int_0^2 x(2x-x^2)dx=\int_0^2 (2x^2-x^3)dx$$
$$=\int_0^2 2x^2dx-\int_0^2x^3dx$$
$$=\dfrac{2x^3}{3}\Big|_0^2-\dfrac{x^4}{4}\Big|_0^2$$
$$\left(\dfrac{2\cdot 2^3}{3}-\dfrac{2\cdot 0^3}{3}\right)-\left(\dfrac{2^4}{4}-\dfrac{0^4}{4}\right)$$
$$=\dfrac{16}{3}-4=\dfrac{4}{3}$$
La integral también se puede calcular haciendo un barrido horizontal, en cuyo caso se integra primero sobre la variable $latex y$, la cual varía entre $latex \dfrac{y}{2}$ y $latex \sqrt {y}$, mientras que $latex y$ varía entre $latex y=0$ y $latex y=4$.
Se deja como ejercicio para el lector comprobar que el resultado es el mismo.
EJERCICIO 7
Hallar:
$$ \iint \limits_{R} x^{2}dx dy $$
Donde R es la región comprendida entre el $latex eje\,X$ y la parábola $latex 4-x^{2}$ en el intervalo $latex x\in [-2,2]$.
Solución
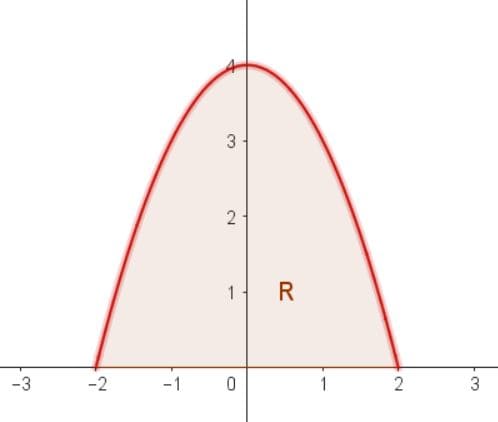
La región de integración se muestra en la figura de arriba.
Para resolver la integral planteada se lleva a cabo un barrido sobre la variable $latex y$, la cual va desde el $latex x$ hasta la parábola.
$$ \displaystyle\iint \limits_{R} x^{2}dx dy=\int_{-2}^{2}x^{2}\left[ \int_{0}^{-x^{2}+4}dy\right] dx$$
La integral entre corchetes resulta:
$$\displaystyle\int_{0}^{-x^{2}+4}dy = 4-x^{2}$$
Enseguida se sustituye en la integral original:
$$\displaystyle \int_{-2}^{2}x^{2}\left( 4-x^{2}\right) dx=\int_{-2}^{2}4x^{2}dx-\int_{-2}^{2}x^{4} dx$$
$$= \frac{4}{3} x^{3}\Big|_{-2}^{+2}-\frac{1}{5}x^{5} \Big|_{-2}^{+2}=\frac{128}{15}$$
EJERCICIO 8
Hallar el volumen del sólido en el primer octante, sobre base rectangular, limitado por:
i) Los planos coordenados
ii) El plano x = 3
iii) El cilindro parabólico $latex z = 4 -y^2$
Solución
El volumen del sólido es la integral bajo $latex z=f(x,y)$, con las paredes dadas por los planos $latex y=0$, $latex z=0$ y $latex x=3$.
El primer paso es determinar las intersecciones de $latex f(x,y)=4-y^2$ con los ejes coordenados, con el fin de encontrar los límites de integración.
Intersección de $latex f(x,y)$ con el eje z
Haciendo $latex y = 0$, se obtiene: $latex z =4-0^2=4$
Por lo tanto, la intersección del cilindro parabólico con el eje $latex z$ es el punto $latex (0,0,4)$
Intersección de $latex f(x,y)$ con el eje y
Haciendo $latex z= 0$, resulta:
$latex 4-y^2=0\Rightarrow y =2$
Se toma la raíz positiva, ya que se busca la intersección con el eje $latex y$ positivo, que es el punto $latex (0,2,0)$.
El plano $latex y=0$ limita al sólido, ya que este se encuentra en el primer octante, según el enunciado, por lo tanto, la base del sólido es un rectángulo de dimensiones $latex x=3$ y $latex y =2$, mientras que las dos paredes restantes están dadas por los planos $latex x=0$ y $latex x=3$.
El sólido resultante se muestra en la siguiente figura:
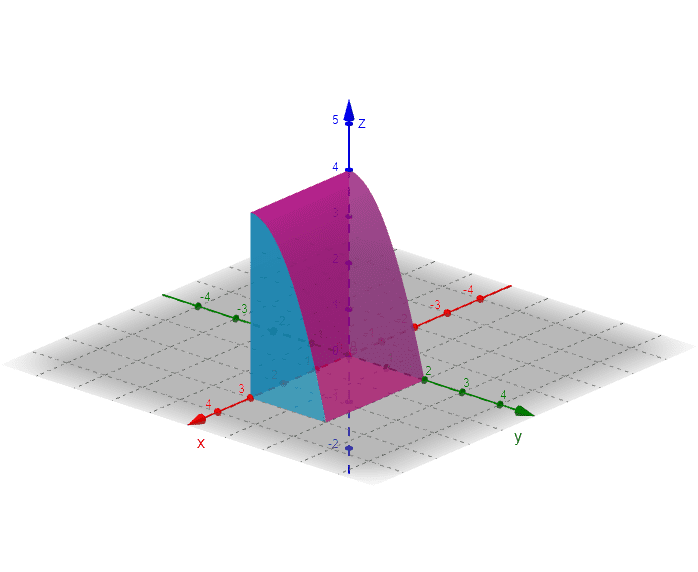
El volumen del sólido corresponde a la integral:
$$V=\int_a^b\int_c^d f(x,y)dydx$$
Donde $latex y$ varía entre $latex 0$ y $latex 2$, mientras que $latex x$ lo hace entre $latex 0$ y $latex 3$, por lo tanto:
$$V=\int_0^3\left[\int_0^2 (4 -y^2)dy\right]dx$$
En primer lugar se calcula la integral interior:
$$\int_0^2 (4 -y^2)dy=\int_0^2 4dy-\int_0^2 y^2dy$$
$$4y\Big|_0^2-\dfrac{y^3}{3}\Big|_0^2$$
$$=8-\dfrac{8}{3}=\dfrac{16}{3}$$
El resultado se sustituye en el corchete de la integral de volumen:
$$V=\int_0^3\left(\dfrac{16}{3}\right) dx$$
$$=\dfrac{16}{3}\int_0^3dx=\left(\dfrac{16}{3}\right)x\Big|_0^3=16$$
EJERCICIO 9
Hallar la integral:
$$ \displaystyle \iint \limits_{R} x \; y \; dx dy $$
Siendo:
$latex R = \{ (x,y) \in \mathbb{R}^{2} / \; 4-2x \leq y \leq 4-x^{2} \} $
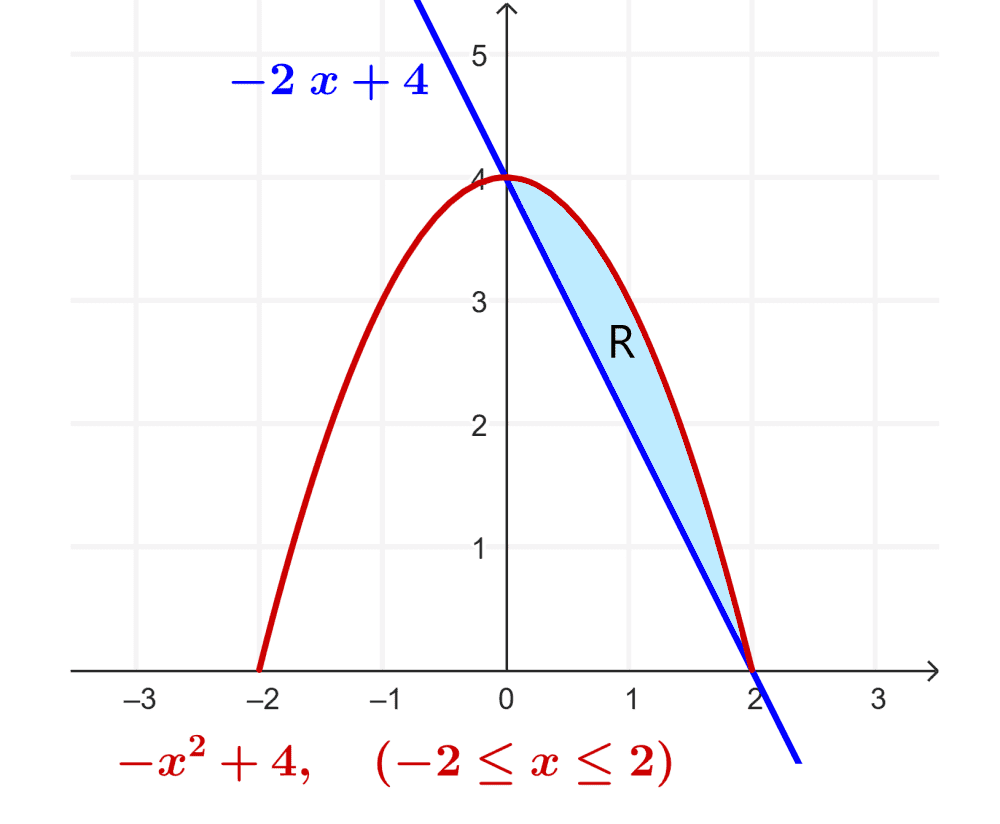
Solución
La integral se puede resolver realizando un barrido vertical en primer lugar, lo cual significa que la integral más interna se lleva a cabo sobre la variable $latex y$.
De la gráfica mostrada, la variable $latex y$ va desde la recta $latex y =4-2x$ hasta la parábola $latex 4-x^{2}$. Las intersecciones de ambas curvas se aprecian en la gráfica, son los puntos $latex (0,4)$ y $latex (2,0)$, por lo tanto, la variable $latex x$ va desde $latex x= 0$, hasta $latex x = 4$:
$$ \displaystyle \iint \limits_{R} x \; y \; dx dy=$$
$$=\displaystyle\int_{0}^{2} \left[\int_{4-2x}^{4-x^{2}} x \; y \; dy \right]dx$$
$$=\int_{0}^{2} \left[ \; x \int_{4-2x}^{4-x^{2}} y dy \;\right] dx $$
La integral entre corchetes es:
$$\left[ \; x \displaystyle\int_{4-2x}^{4-x^{2}} ydy \; \right]= \dfrac{1}{2}x^{2} ( x-2 ) ^{2} ( x+4 ) $$
Y sustituyendo este resultado en la integral correspondiente a la variable $latex x$ se obtiene:
$$\displaystyle\int_{0}^{2}\left[\;\dfrac{1}{2}x^{2}( x-2) ^{2} ( x+4) \;\right]dx=\int_{0}^{2} \left( \dfrac{1}{2}x^{5}-6x^{3}+8x^{2} \right) dx$$
$$=\left[\dfrac{x^6}{12}-\dfrac{6x^4}{4}+\dfrac{8x^3}{3}\right]_0^2=\frac{8}{3}$$
EJERCICIO 10
Calcular el volumen del sólido limitado por las superficies $latex z=4-x^2-2y^2$ y el plano $latex z=2$.
Solución
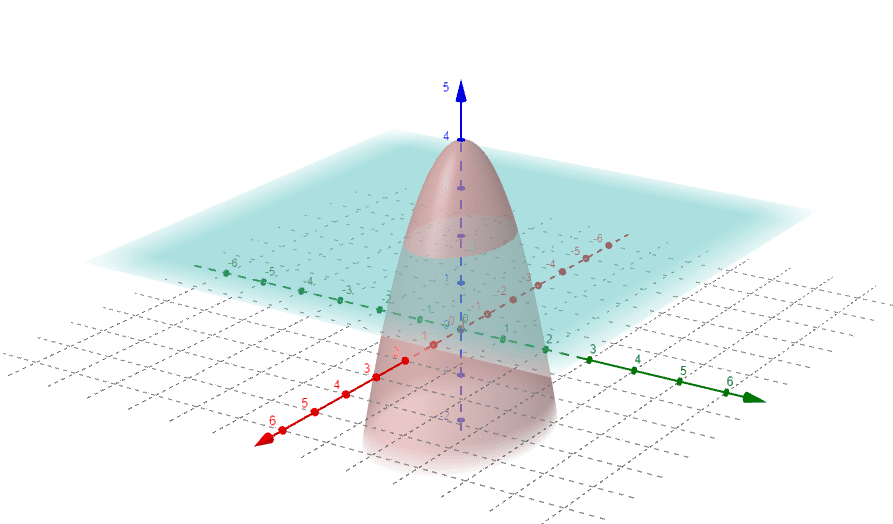
El volumen a calcular está por debajo del paraboloide y por encima del plano $latex z=2$, como se muestra en la figura de arriba. Viene dado por la integral doble:
$$V=\displaystyle\iint_R \left[f(x,y)-g(x,y)\right ]dxdy$$
Donde R es la superficie proyectada sobre el plano $latex xy$. En el ejemplo:
- $latex f(x,y) =4-x^2-2y^2$
- $latex g(x,y) =2$
Por lo tanto:
$$V=\displaystyle\iint_R \left[(4-x^2-2y^2)-2\right]dxdy$$
Ahora hay que encontrar la región de integración $latex R$, limitada por la curva que resulta de la intersección de las superficies. Esta se obtiene igualando $latex f(x,y)=g(x,y)$:
$$4-x^2-2y^2=2$$
$$\Rightarrow -x^2-2y^2=-2= x^2+2y^2=2$$
Dividiendo entre $latex 2$:
$$\dfrac{x^2}{2}+\dfrac{y^2}{1}=1$$
La curva de intersección es una elipse.
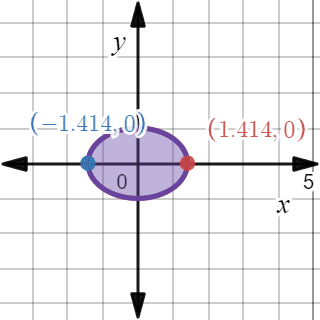
Las intersecciones de dicha elipse con el eje $latex x$ son $latex (-\sqrt{2},0)$ y $latex (\sqrt{2},0)$.
Se puede hacer un barrido sobre la variable $latex y$ sobre el primer cuadrante, de manera que el volumen queda así:
$$V=\displaystyle 4\int_ {0}^{\sqrt{2}}\int_ {0}^{\sqrt{1-\frac{x^2}{2}}}\left[(4-x^2-2y^2)-2\right]dxdy=$$
$$=\displaystyle 4\int_ {0}^{\sqrt{2}}\left[\int_ {0}^{\sqrt{1-\frac{x^2}{2}}}(2-x^2-2y^2) dy\right]dx$$
La integral entre corchetes es:
$$\displaystyle \int_ {0}^{\sqrt{1-\frac{x^2}{2}}}(2-x^2-2y^2) dy=$$
$$= (2-x^2)\int_ {0}^{\sqrt{1-\frac{x^2}{2}}}dy-2\int_ {0}^{\sqrt{1-\frac{x^2}{2}}}y^2dy$$
$$=(2-x^2)\left(\sqrt{1-\frac{x^2}{2}}\right)-\dfrac{2}{3}\sqrt{\left(1-\frac{x^2}{2}\right)^3}$$
$$=\dfrac{(2-x^2)}{\sqrt 2}\sqrt{2-x^2}-\dfrac{2}{6\sqrt2}\sqrt{\left(2-x^2\right)^3}$$
$$=\dfrac{1}{\sqrt2}\sqrt{\left(2-x^2\right)^3}-\dfrac{2}{6\sqrt2}\sqrt{\left(2-x^2\right)^3}$$
$$=\left(\dfrac{1}{\sqrt2}-\dfrac{1}{3\sqrt2}\right)\sqrt{\left(2-x^2\right)^3}$$
$$=\dfrac{2}{3\sqrt2}\sqrt{\left(2-x^2\right)^3}$$
El resultado se sustituye en la integral de volumen:
$$V=\displaystyle 4\int_ {0}^{\sqrt{2}}\dfrac{2}{3\sqrt2}\sqrt{\left(2-x^2\right)^3}dx$$
Esta integral se resuelve mediante la sustitución trigonométrica:
- $latex x=\sqrt{2}\sin u$
- $latex dx=\sqrt{2}\cos u du$
Los nuevos límites de integración se calculan así:
Para $latex {x =0}$
$latex \sqrt{2}\sin u=0\Rightarrow \sin u=0\Rightarrow u = 0$
Para $latex {x =\sqrt{2}}$
$latex \sqrt{2}\sin u=\sqrt{2}\Rightarrow \sin u=1\Rightarrow u = \dfrac{\pi}{2}$
$$V=\displaystyle\dfrac{8}{3\sqrt2} \int_ {0}^{\frac{\pi}{2}}\sqrt{\left(2-2\sin^2u\right)^3}\sqrt{2}\cos u du=$$
$$=\displaystyle\dfrac{16\sqrt2}{3} \int_ {0}^{\frac{\pi}{2}}\sqrt{\left(1-\sin^2u\right)^3}\cos u du=\dfrac{16\sqrt2}{3} \int_ {0}^{\frac{\pi}{2}}\cos^4 u du$$
Utilizando:
$$\displaystyle\int \cos^n x dx=\dfrac{\cos^{n-1}x\sin x}{n}+\dfrac{n-1}{n}\int\cos^{n-2}dx$$
Queda:
$$\displaystyle\int \cos^4 x dx=\dfrac{\cos^{3}x\sin x}{4}+\dfrac{3}{4}\int\cos^{2}xdx$$
$$=\dfrac{\cos^{3}x\sin x}{4}+\dfrac{3}{8}(x+\cos x \sin x)+C$$
Entonces:
$$V=\dfrac{16\sqrt2}{3} \left[\dfrac{\cos^{3}u\sin u}{4}+\dfrac{3}{8}(u+\cos u \sin u)\right]_0^{\frac{\pi}{2}}$$
$$=\sqrt 2\pi$$
Ejercicios de integrales dobles para resolver


Encuentra la integral de $latex f(x,y)=x^2-y^2$ sobre el rectángulo con los límites $latex 1\leq x\leq 3$ y $latex 0\leq y\leq 2$.
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre integrales? Puedes mirar estas páginas:
–


