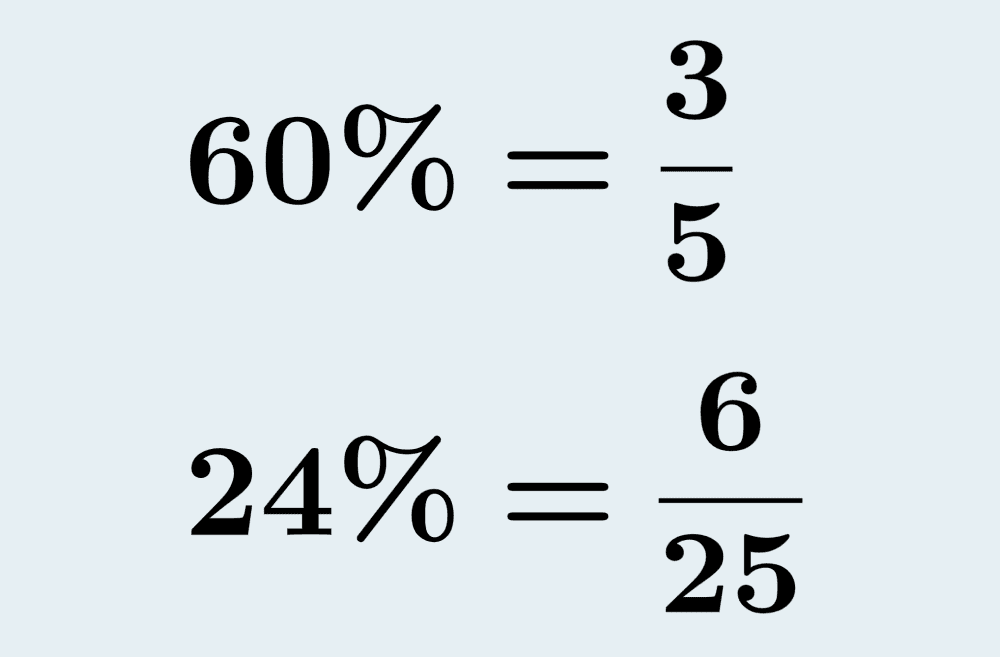Los porcentajes pueden ser convertidos a fracciones al escribir al porcentaje como el numerador y escribir a 100 como el denominador. Luego, simplificamos para obtener la fracción final.
A continuación, conoceremos cómo convertir porcentajes a fracciones paso a paso. Luego, aplicaremos todo lo aprendido al resolver algunos ejercicios y problemas de práctica.
¿Cómo convertir porcentajes a fracciones?
Para convertir porcentajes a fracciones, escribimos al porcentaje como el numerador y a 100 como el denominador y luego, simplificamos.
Supongamos que queremos escribir a 45% como fracción. Podemos seguir los siguientes pasos:
Paso 1: Escribe el valor porcentual como el numerador (número superior) de la fracción.
En este caso, el numerador es 45.
Paso 2: Escribe 100 como el denominador (número inferior) de la fracción, ya que un porcentaje representa una parte sobre 100:
$$45\%=\frac{45}{100}$$
Paso 3: Simplifica la fracción hallando el máximo común divisor (MCD) del numerador y el denominador y dividiendo ambos números por el MCD.
El MCD de 45 y 100 es 5, así que dividimos al numerador y al denominador por 5:
$$\frac{45}{100}=\frac{9}{20}$$
Entonces, 45% es igual a $latex \frac{9}{20}$.
10 Ejercicios resueltos de convertir porcentajes a fracciones
EJERCICIO 1
Escribe a 60% como una fracción.
Solución
Paso 1: Escribe el valor porcentual como numerador: 60
Paso 2: Escribe 100 como denominador:
$$60\%=\frac{60}{100}$$
Paso 3: El MCD de 60 y 100 es 20, así que dividimos al numerador y al denominador por 20:
$$\frac{60}{100}=\frac{3}{5}$$
Solución: 60% en fracción es $latex \frac{3}{5}$.
EJERCICIO 2
Convierte a 75% a una fracción.
Solución
Paso 1: El numerador es 75.
Paso 2: El denominador es 100:
$$75\%=\frac{75}{100}$$
Paso 3: El MCD de 75 y 100 es 25, así que divide el numerador y el denominador por 25:
$$\frac{75}{100}=\frac{3}{4}$$
Solución: 75% en fracción es $latex \frac{3}{4}$.
EJERCICIO 3
¿Cuál fracción es igual a 12%?
Solución
Paso 1: El numerador es 12.
Paso 2: El denominador es 100:
$$12\%=\frac{12}{100}$$
Paso 3: El MCD de 12 y 100 es 4. Entonces, dividimos al numerador y al denominador por 4:
$$\frac{12}{100}=\frac{3}{25}$$
Solución: 12% en fracción es $latex \frac{3}{25}$.
EJERCICIO 4
Encuentra una fracción equivalente a 20%.
Solución
Paso 1: Escribe el valor porcentual como numerador: 20
Paso 2: Escribe 100 como denominador:
$$20\%=\frac{20}{100}$$
Paso 3: El MCD de 20 y 100 es 20, así que simplificamos de la siguiente forma:
$$\frac{1}{5}$$
Solución: 20% en fracción es $latex \frac{1}{5}$.
EJERCICIO 5
Escribe a 35% como una fracción.
Solución
Paso 1: El numerador es 35.
Paso 2: El denominador es 100:
$$35\%=\frac{35}{100}$$
Paso 3: El MCD de 35 y 100 es 5. Al simplificar, tenemos:
$$\frac{35}{100}=\frac{7}{20}$$
Solución: 35% en fracción es $latex \frac{7}{20}$.
EJERCICIO 6
Convierte a 7% como una fracción.
Solución
Paso 1: El numerador de la fracción es 7.
Paso 2: Escribe al 100 como denominador:
$$7\%=\frac{7}{100}$$
Paso 3: 7 es un número primo, por lo que la fracción ya está en su forma más simple.
Solución: 7% en fracción es $latex \frac{7}{100}$.
EJERCICIO 7
¿Cuál fracción es igual a 37.5%?
Solución
Paso 1: El valor porcentual es el numerador: 37.5
Paso 2: 100 es el denominador:
$$37.5\%=\frac{37.5}{100}$$
Paso 3: En primer lugar, eliminamos el decimal multiplicando por 10 al numerador y al denominador:
$$\frac{37.5}{100}=\frac{375}{1000}$$
El MCD de 375 y 1000 es 125, así que dividimos al numerador y al denominador por 125:
$$\frac{375}{1000}=\frac{3}{8}$$
Solución: 37.5% en fracción es $latex \frac{3}{8}$.
EJERCICIO 8
Escribe a 2.5% como una fracción.
Solución
Paso 1: El numerador es 2.5
Paso 2: El denominador es 100:
$$2.5\%=\frac{2.5}{100}$$
Paso 3: Podemos eliminar el decimal multiplicando por 10 al numerador y al denominador:
$$\frac{2.5}{100}=\frac{25}{1000}$$
El MCD de 25 y 1000 es 25, así que dividimos al numerador y al denominador por 25:
$$\frac{25}{1000}=\frac{1}{40}$$
Solución: 2.5% en fracción es $latex \frac{1}{40}$.
EJERCICIO 9
Encuentra una fracción equivalente a 66.67%.
Solución
Paso 1: El numerador de la fracción es 66.67.
Paso 2: El denominador es 100:
$$66.67\%=\frac{66.67}{100}$$
Paso 3: Para eliminar el decimal multiplicamos tanto al numerador como al denominador por 100:
$$\frac{66.67}{100}=\frac{6667}{10000}$$
6667 es un número primo, por lo que la fracción ya está en su forma más simple.
Solución: 66.67% en fracción es $latex \frac{6667}{10000}$.
EJERCICIO 10
Convierte a 12.5% a una fracción.
Solución
Paso 1: El numerador es 12.5.
Paso 2: El denominador es 100:
$$12.5\%=\frac{12.5}{100}$$
Paso 3: Empezamos eliminando el decimal al multiplicar por 10 tanto al numerador y al denominador:
$$\frac{12.5}{100}=\frac{125}{1000}$$
El MCD de 125 y 1000 es 125, así que dividimos al numerador y al denominador por 125:
$$\frac{125}{1000}=\frac{1}{8}$$
Solución: 12.5% en fracción es $latex \frac{1}{8}$.
Ejercicios de convertir porcentajes a fracciones para resolver
Al convertir a 62.5% a fracción., ¿cuál es el numerador de la forma más simplificada?
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre convertir fracciones, decimales y porcentajes? Puedes mirar estas páginas:
–
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
