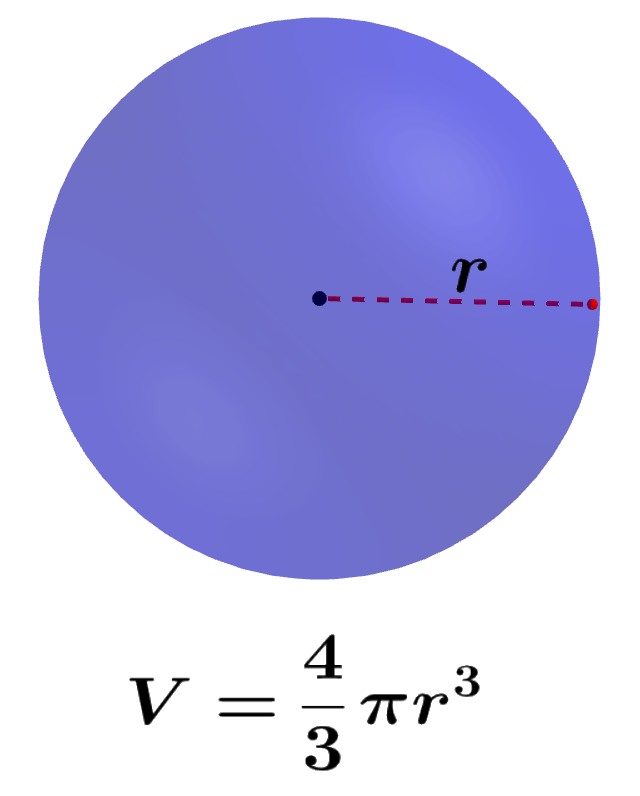
El volumen de una esfera es igual al espacio ocupado por la esfera en las tres dimensiones. El volumen de una esfera depende de su radio ya que, si es que tomamos la sección transversal de la esfera, tenemos un círculo. Entonces, tenemos que usar la longitud del radio para calcular su volumen. Alternativamente, también podemos calcular su volumen usando el diámetro ya que simplemente es el doble del radio.
A continuación, conoceremos las fórmulas que podemos usar para calcular el volumen de esferas usando tanto su radio, como su diámetro. Además, también aprenderemos a calcular el volumen de esferas huecas. Finalmente, aplicaremos todas las fórmulas aprendidas para resolver algunos ejercicios.
Fórmula del volumen de una esfera
La esfera está definida como una figura sólida tridimensional, en la que cada punto en su superficie es equidistante del centro. La distancia fija es llamada el radio de la esfera y el punto fijo es llamado el centro de la esfera.
El volumen de una esfera es determinado usando la longitud del radio y la siguiente fórmula:
| $latex V=\frac{4}{3}\pi {{r}^3}$ |
en donde, r es la longitud del radio de la esfera.
Esta fórmula es derivada usando métodos de integración.
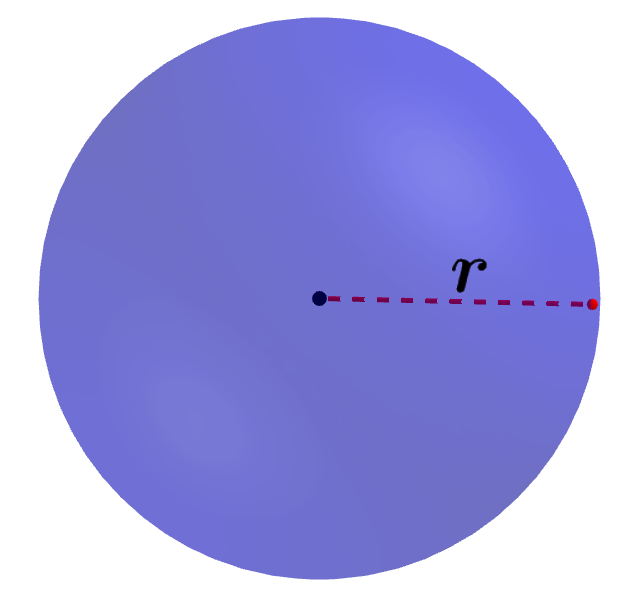
Volumen de una esfera usando el diámetro
Alternativamente, podemos usar el diámetro de una esfera para calcular su volumen. Podemos realizar esto usando dos métodos diferentes.
El primer método consiste en recordar que el diámetro de una esfera es igual a 2r, en donde r es la longitud del radio de la esfera. Entonces, si es que tenemos la longitud del diámetro, podemos dividir por dos para obtener la longitud del radio y usar la fórmula del volumen dada arriba.
El segundo método consiste en escribir a la fórmula del volumen en términos del diámetro de la esfera. Si es que hacemos esto, tenemos:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(\frac{d}{2})}^3}$
$latex V=\frac{4}{3}\pi (\frac{{{d}^3}}{8})$
$latex V=\frac{4}{24}\pi {{d}^3}$
| $latex V=\frac{1}{6}\pi {{d}^3}$ |
en donde, d es la longitud del diámetro.
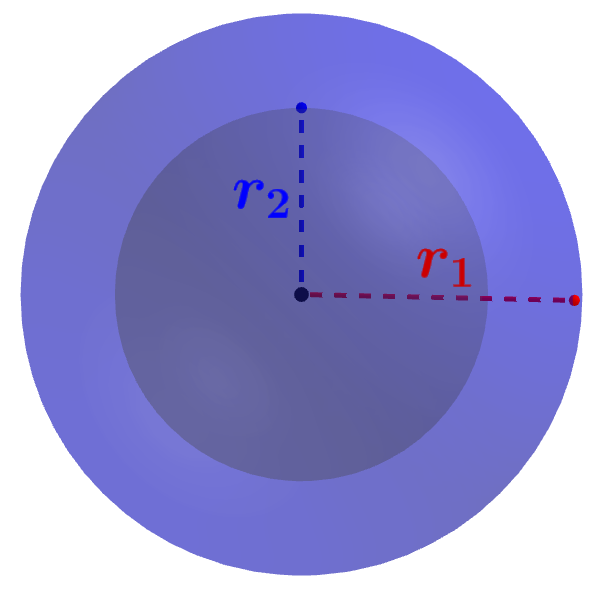
Volumen de una esfera hueca
El volumen de esferas huecas es calculado al sustraer el volumen de la parte hueca del volumen de la esfera completa. Entonces, si es que usamos a $latex r_{1}$ para representar al radio de la esfera completa y a $latex r_{2}$ para representar al radio interno, es decir, el radio de la parte hueca, tenemos:
$latex V=\frac{4}{3}\pi {{r_{1}}^3}-\frac{4}{3}\pi {{r_{2}}^3}$
Podemos simplificar esto para obtener la siguiente fórmula:
| $latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$ |
Ejercicios de volumen de una esfera resueltos
Los siguientes ejercicios son resueltos usando las fórmulas del volumen de esferas vistas arriba. Cada ejercicio tiene su respectiva solución, en donde se detalla el proceso y razonamiento usados.
EJERCICIO 1
¿Cuál es el volumen de una esfera que tiene un radio de 3 m?
Solución
Usamos la primera fórmula del volumen con $latex r=3$:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(3)}^3}$
$latex V=\frac{4}{3}\pi (27)$
$latex V=113.1$
El volumen es igual a 113.1 m³.
EJERCICIO 2
Una esfera tiene un radio de 4 m. ¿Cuál es su volumen?
Solución
Tenemos que usar la primera fórmula del volumen con la longitud $latex r=4$:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(4)}^3}$
$latex V=\frac{4}{3}\pi (64)$
$latex V=268.1$
El volumen es igual a 268.1 m³.
EJERCICIO 3
¿Cuál es el volumen de una esfera que tiene un diámetro de 5 m?
Solución
En este caso, tenemos el diámetro de la esfera, por lo que tenemos que dividir por 2 y usar la fórmula del volumen. Esto significa que el radio es $latex r=2.5$:
$latex V=\frac{4}{3}\pi {{r}^3}$
$latex V=\frac{4}{3}\pi {{(2.5)}^3}$
$latex V=\frac{4}{3}\pi (6.25)$
$latex V=26.2$
El volumen es igual a 26.2 m³.
EJERCICIO 4
¿Cuál es el volumen de una esfera hueca que tiene un radio externo de 6 m y un radio interno de 4 m?
Solución
Tenemos una esfera hueca con los radios $latex r_{1}=6$ y $latex r_{2}=4$. Entonces, usamos la tercera fórmula del volumen con estos radios:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(6)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (216-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=636.7$
El volumen es igual a 636.7 m³.
EJERCICIO 5
Una esfera hueca tiene un radio externo de longitud 5 m y un radio interno de longitud 4 m. ¿Cuál es su volumen?
Solución
Los radios de la esfera hueca son $latex r_{1}=5$ y $latex r_{2}=4$. Entonces, usamos estos valores en la fórmula del volumen de una esfera hueca:
$latex V=\frac{4}{3}\pi ({{r_{1}}^3}-{{r_{2}}^3})$
$latex V=\frac{4}{3}\pi ({{(5)}^3}-{{(4)}^3})$
$latex V=\frac{4}{3}\pi (125-64)$
$latex V=\frac{4}{3}\pi (152)$
$latex V=255.5$
El volumen es igual a 255.5 m³.
Ejercicios de volumen de esferas para resolver
Pon en práctica el uso de las fórmulas del volumen vistas arriba para resolver los siguientes ejercicios. Selecciona tu respuesta y verifícala para comprobar que obtuviste la respuesta correcta.
Véase también
¿Interesado en aprender más sobre esferas? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
