Un triángulo escaleno obtusángulo es un triángulo escaleno que tiene un ángulo interno obtuso. Estos triángulos son escalenos y obtusángulos al mismo tiempo. Recordemos que un ángulo obtuso es un ángulo que es mayor que 90 grados y un triángulo escaleno es un triángulo que tiene todos sus lados con longitudes diferentes y todos sus ángulos con medidas diferentes.
A continuación, aprenderemos más sobre los triángulos escalenos obtusángulos. Conoceremos algunas de sus características y de sus fórmulas más importantes. Además, usaremos esas fórmulas para resolver algunos ejercicios.
¿Qué son los triángulos escalenos obtusángulos?
Un triángulo escaleno obtusángulo es un triángulo que es escaleno y obtusángulo al mismo tiempo. Los triángulos escalenos se caracterizan por tener lados de longitudes diferentes, es decir, ningún lado de un triángulo escaleno es igual a otro.
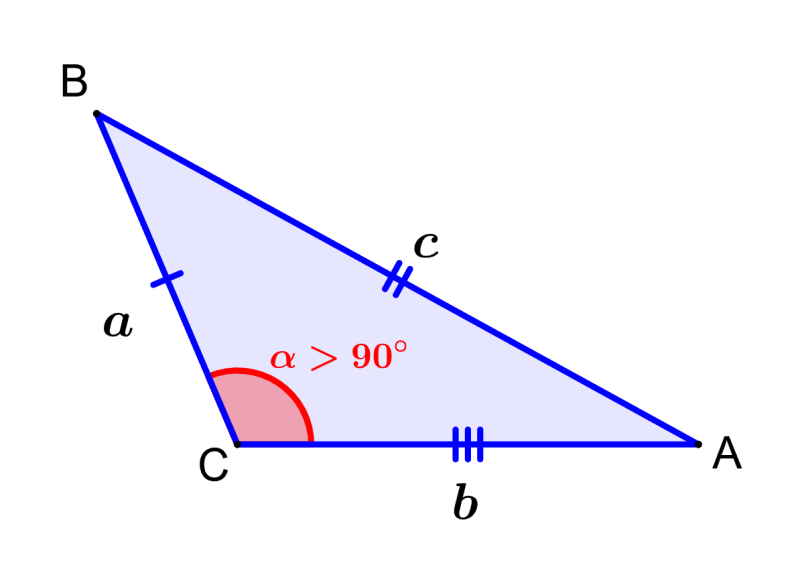
Además, los ángulos escalenos también tienen ángulos que son diferentes el uno del otro. Un triángulo obtusángulo se caracteriza por tener un ángulo interno mayor que 90 grados. El siguiente es un ejemplo de un triángulo escaleno obtusángulo:
Fórmulas de importantes de triángulos escalenos
Los triángulos escalenos obtusángulos tienen las mismas fórmulas importantes que los triángulos escalenos “normales”.
Área de triángulos escalenos
Podemos calcular el área de triángulos escalenos al multiplicar al producto de la base y la altura por un medio:
| $latex A=\frac{1}{2}\times b \times h$ |
en donde, b representa a la longitud de la base y h representa a la longitud de la altura.
Perímetro de triángulos escalenos
El perímetro de triángulos escalenos es igual a la suma de las longitudes de todos sus lados:
| $latex p=a+b+c$ |
en donde, $latex a,~b,~c$ representan a las longitudes de los lados del triángulo escaleno obtusángulo.
Ejemplos de problemas con triángulos escalenos
EJEMPLO 1
- Tenemos un triángulo escaleno con una base de 16 m y una altura de 18 m. ¿Cuál es su área?
Solución: Podemos usar la fórmula del área con la información dada:
$latex A=\frac{1}{2}\times b \times h$
$latex A=\frac{1}{2}\times 16 \times 18$
$latex A=144$
El área es 144 m².
EJEMPLO 2
- ¿Cuál es el perímetro de un triángulo escaleno que tiene lados de longitudes 21 m, 23 m, 26 m?
Solución: Reemplazamos las longitudes de los lados en la fórmula del perímetro:
$latex p=a+b+c$
$latex p=21+23+26$
$latex p=70$
El perímetro es 70 m.
EJEMPLO 3
- ¿Cuál es la longitud de la altura de un triángulo si es que su área es 50 m² y su base mide 10?
Solución: Usamos la fórmula del área y resolvemos para h que es la altura:
$latex A=\frac{1}{2}\times b\times h$
$latex 50=\frac{1}{2}\times 10\times h$
$latex 50=5h$
$latex h=10$
La altura mide 10 m.
Ejercicios de triángulos escalenos para resolver
Véase también
¿Interesado en aprender más sobre triángulos escalenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
