Los triángulos escalenos acutángulos son triángulos escalenos en los que todos sus ángulos internos son agudos. Estos triángulos satisfacen la definición de un triángulo escaleno y un triángulo obtuso al mismo tiempo. Recordemos que un ángulo agudo es un ángulo que es menor que 90 grados y los triángulos escalenos son triángulos que tienen lados de diferentes longitudes y ángulos de diferentes longitudes.
A continuación, conoceremos más detalles sobre los triángulos escalenos acutángulos. Aprenderemos sobre sus características importantes y veremos sus fórmulas. Además, resolveremos algunos ejercicios usando estas fórmulas.
¿Qué son los triángulos escalenos acutángulos?
Los triángulos escalenos acutángulos son triángulos que son escalenos y acutángulos al mismo tiempo. Esto significa que estos triángulos cumplen con las condiciones de un triángulo escaleno y de un triángulo acutángulo.
Los triángulos escalenos tienen la condición de tener todos los lados de longitudes diferentes y todos los ángulos de medidas diferentes. En un triángulo escaleno, ningún lado es igual a otro y ningún ángulo es igual a otro.
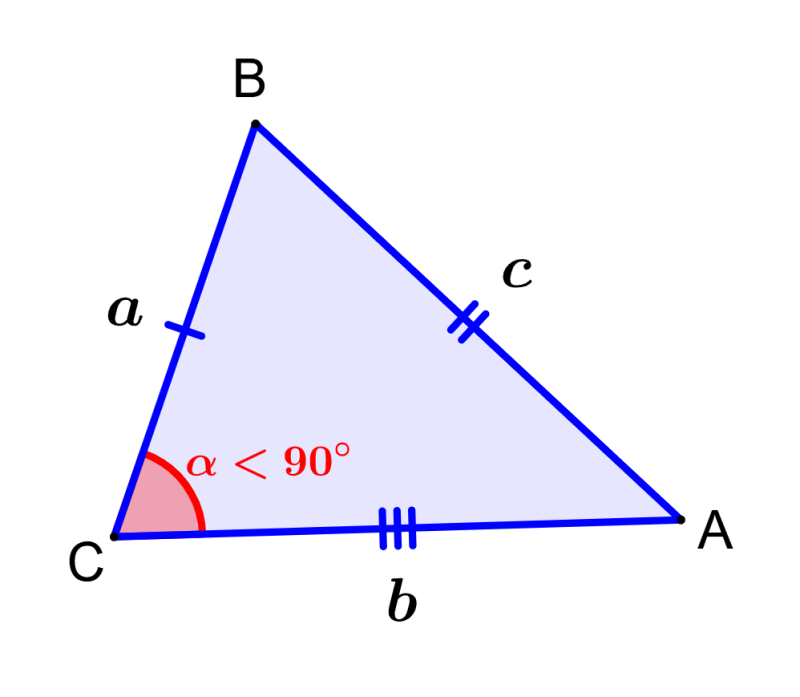
Un triángulo acutángulo tiene la condición de que todos sus ángulos internos son agudos, es decir, menores que 90 grados. El siguiente es un ejemplo de un triángulo escaleno acutángulo:
Fórmulas más usadas de triángulos escalenos
Podemos usar las mismas fórmulas que usamos con los triángulos escalenos “normales” para resolver problemas de triángulos escalenos acutángulos.
Área de triángulos escalenos
El área de un triángulo escaleno es calculada usando las longitudes de la base y de la altura:
| $latex A=\frac{1}{2}\times b \times h$ |
Aquí, b es la longitud de la base y h representa a la longitud de la altura.
Perímetro de triángulos escalenos
Si es que conocemos la longitud de los lados del triángulo escaleno, su perímero simplemente es la suma de las longitudes:
| $latex p=a+b+c$ |
Aquí, $latex a,~b,~c$ son las longitudes de los lados del triángulo escaleno acutángulo.
Ejemplos resueltos de triángulos escalenos
EJEMPLO 1
- Si es que un triángulo escaleno tiene una base de 20 m y una altura de 22 m, ¿cuál es su área?
Solución: Usamos la información dada en la fórmula del área:
$latex A=\frac{1}{2}\times b \times h$
$latex A=\frac{1}{2}\times 20 \times 22$
$latex A=220$
El área es 220 m².
EJEMPLO 2
- Un triángulo escaleno tiene lados de longitudes 31 m, 33 m y 34 m. ¿Cuál es su perímetro?
Solución: Usamos la fórmula del perímetro con estas longitudes:
$latex p=a+b+c$
$latex p=31+33+34$
$latex p=98$
El perímetro es 98 m.
EJEMPLO 3
- Un triángulo escaleno tiene un área de 64 m² y su base mide 20. ¿Cuál es la longitud de su altura?
Solución: Usamos esta información para sustituir en la fórmula del área y resolver para h:
$latex A=\frac{1}{2}\times b\times h$
$latex 64=\frac{1}{2}\times 20\times h$
$latex 64=10h$
$latex h=6.4$
La altura mide 6.4 m.
Ejercicios de triángulos escalenos para resolver
Véase también
¿Interesado en aprender más sobre triángulos escalenos? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
