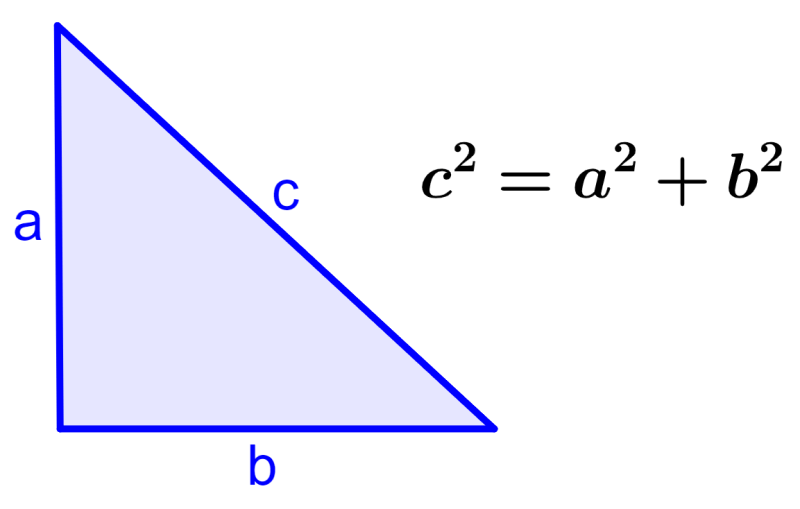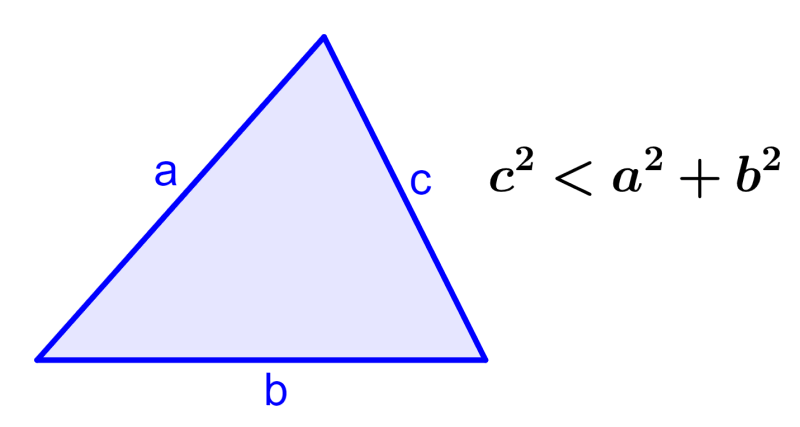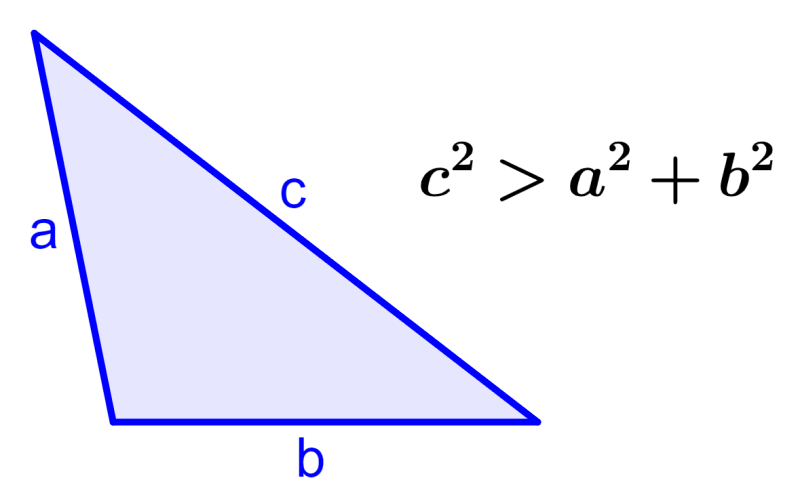El teorema de Pitágoras es el más usado en trigonometría y nos permite calcular la longitud de uno de los lados si es que conocemos la longitud de los otros dos lados. Por otra parte, el teorema inverso al teorema de Pitágoras nos permite determinar si un triángulo es rectángulo, agudo u obtuso al comparar la suma de los cuadrados de los catetos con el cuadrado de la hipotenusa.
En este artículo, miraremos una definición detallada del teorema inverso al teorema de Pitágoras. Luego, aprenderemos cómo demostrar este teorema inverso y lo aplicaremos para resolver algunos ejercicios de práctica.
¿Qué es el teorema inverso al de Pitágoras?
El teorema inverso al teorema de Pitágoras indica que, «Si es que tenemos a²+b²=c² en un triángulo con lados a, b, y c, el ángulo entre a y b mide 90° y el triángulo es un triángulo rectángulo.»
También podemos usar el teorema inverso al de Pitágoras para determinar si es que un triángulo es obtuso o agudo. Entonces, para un triángulo que tiene los lados a, b, y c, en donde c es la hipotenusa, tenemos:
1. Si es que tenemos c²<a²+b², el ángulo opuesto al lado c es agudo y el triángulo es un triángulo agudo.
2. Si es que tenemos c²=a²+b², el ángulo opuesto al lado c es recto y el triángulo es un triángulo rectángulo.
3. Si es que tenemos c²>a²+b², el ángulo opuesto al lado c es obtuso y el triángulo es un triángulo obtuso.
Demostración del teorema inverso al teorema de Pitágoras
Para demostrar el teorema inverso al de Pitágoras, vamos a usar dos triángulos.
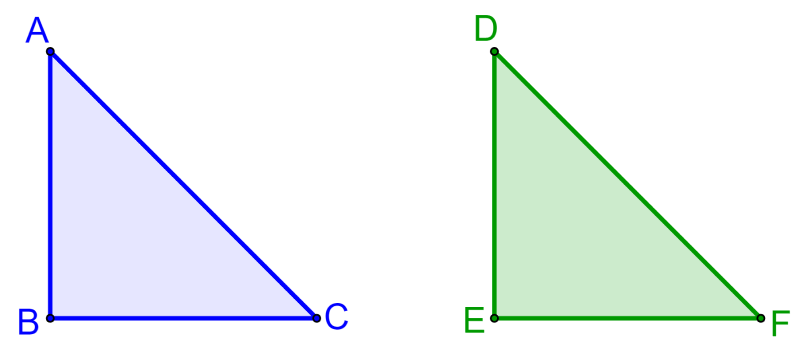
Primero, tenemos al triángulo ABC, en el cual tenemos AC²=AB²+BC². Para demostrar el teorema inverso, tenemos que probar que ∠B = 90°.
Luego, construimos a un triángulo rectángulo DEF con un ángulo recto en E. Es decir, tenemos ∠E=90°. Además, este triángulo cumple con la condición de que DE=AB y EF=BC.
En el triángulo DEF, podemos usar el teorema de Pitágoras, ya que ∠E = 90°. Entonces, tenemos:
DF²=DE²+EF²
Dado que DE=AB y EF=BC, podemos sustituir para obtener:
DF²=AB²+BC²
Dado que tenemos AC²=AB²+BC² del primer triángulo, podemos observar que:
AC²=DF²
AC=DF
Entonces, tenemos que todos los lados de los dos triángulos son iguales. Esto significa que los triángulos ABC y DEF son congruentes (por el criterio lado-lado-lado).
Dado que los triángulos son congruentes, los ángulos correspondientes son iguales. Entonces, tenemos:
∠B = ∠E
Sabemos que el ángulo E mide 90°, por lo que el ángulo B también mide 90° y hemos demostrado el teorema inverso al teorema de Pitágoras.
Ejemplos resueltos del teorema inverso al teorema de Pitágoras
Los siguientes ejemplos son resueltos usando el teorema inverso al teorema de Pitágoras. Intenta resolver los ejercicios tú mismo antes de mirar la solución.
EJEMPLO 1
Un triángulo tiene lados de longitudes 3, 5, 6 unidades. Determina si es que el triángulo es obtuso, rectángulo o agudo.
Solución
Podemos observar que 6 es el lado más largo. Entonces, podemos escribir:
c²=a²+b²
(6)²=(3)²+(5)²
36=9+25
36=34
Entonces, tenemos (6)²>(3)²+(5)². Esto significa que el triángulo es obtuso.
EJEMPLO 2
Un triángulo tiene lados de longitudes 6, 8 y 10 unidades. ¿Es el triángulo agudo, obtuso o rectángulo?
Solución
En este caso, el lado más largo es 10. Entonces, tenemos:
c²=a²+b²
(10)²=(6)²+(8)²
100=36+64
100=100
Entonces, tenemos (10)²=(6)²+(8)². Esto significa que el triángulo es rectángulo.
EJEMPLO 3
Determina si el triángulo con lados 6, 7, 9 unidades es agudo, obtuso o rectángulo.
Solución
El lado más largo es 9. Entonces, tenemos:
c²=a²+b²
(9)²=(6)²+(7)²
81=36+49
81=85
Entonces, tenemos (9)²<(6)²+(7)². Esto significa que el triángulo es agudo.
EJEMPLO 4
Determina si el triángulo con lados 10, 12, 15 unidades es rectángulo o no.
Solución
El lado más largo es 15. Entonces, tenemos:
c²=a²+b²
(15)²=(10)²+(12)²
225=100+144
225=244
Esto significa que el triángulo no es rectángulo.
Ejercicios del teorema inverso al de Pitágoras para resolver
Aplica lo aprendido sobre el teorema inverso al de Pitágoras y resuelve los siguientes ejercicios. Haz clic en «Verificar» para comprobar tu respuesta.
Véase también
¿Interesado en aprender más sobre el teorema de Pitágoras? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
