La suma de una progresión geométrica infinita puede ser calculada cuando la razón común es un número menor que 1 y mayor que -1. Para esto, simplemente necesitamos el valor del primer término y el valor de la razón común. Luego, usamos estos valores en una fórmula estándar.
A continuación, conoceremos la fórmula que podemos usar para encontrar la suma de una progresión geométrica infinita. Luego, aplicaremos esta fórmula para resolver algunos ejercicios.
ÁLGEBRA
Relevante para…
Aprender a encontrar la suma de una progresión geométrica infinita.
ÁLGEBRA
Relevante para…
Aprender a encontrar la suma de una progresión geométrica infinita.
Fórmula para la suma de una progresión geométrica infinita
La suma de una progresión geométrica infinita puede ser calculada cuando tenemos $latex -1<r<1$. Por ejemplo, consideremos la siguiente progresión:
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…\left(\frac{1}{2}\right)^n$$
Podemos observar que, a medida que el número de términos incrementa, el valor de cada término se hace más y más pequeño.
Es decir, a medida que $latex n \rightarrow \infty$, el término $latex \left(\frac{1}{2}\right)^n\rightarrow 0$, por lo tanto, la suma de la progresión tiene un valor específico.
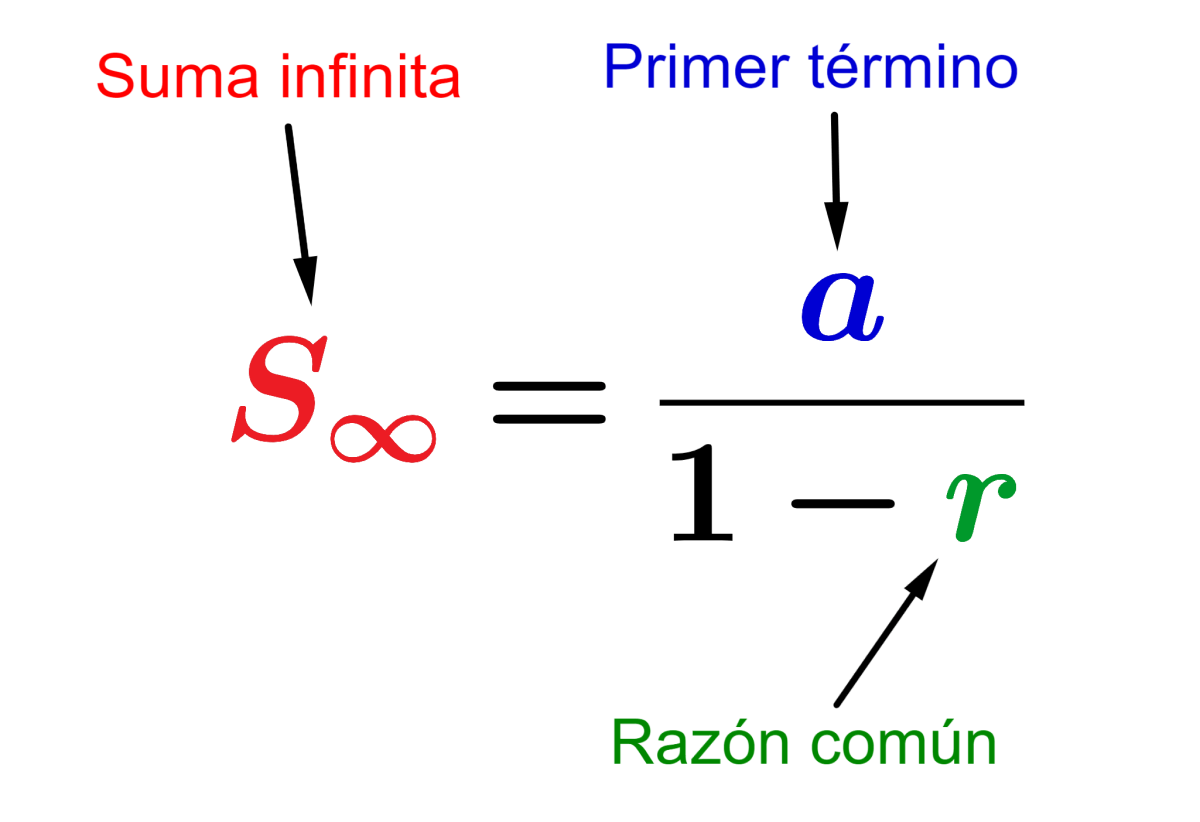
Para encontrar la suma de una progresión geométrica infinita, usamos la siguiente fórmula:
$$S_{\infty}= \frac{a}{1-r}$$
en donde $latex -1<r<1$. Si es que la razón común no cumple con esta condición, la suma infinita no existe.
Demostración de la fórmula de la suma de progresiones geométricas infinitas
Recordemos que podemos encontrar la suma de los primeros $latex n$ términos de cualquier progresión geométrica usando la siguiente fórmula:
$$S_{n}=\frac{a(1-r^n)}{1-r}$$
Si es que la razón común cumple con la condición $latex -1<r<1$, a medida que $latex n\rightarrow \infty$, tenemos $latex r^n\rightarrow 0$.
Básicamente, esto significa que el término $latex r^n$ de la progresión se hace más y más pequeño hasta que su valor se acerca más y más a 0.
Entonces, a medida que $latex n\rightarrow \infty$, tenemos:
$$S_{n}\rightarrow \frac{a(1-0)}{1-r}=\frac{a}{1-r}$$
Por lo tanto, demostramos que la suma infinita de una progresión geométrica en donde $latex -1<r<1$ está dada por:
$$S_{\infty}=\frac{a}{1-r}$$
Observamos que la demostración empieza asumiendo que $latex -1<r<1$. Si es que este no es el caso, la suma infinita no existe.
Ejemplos resueltos de la suma de progresiones geométricas infinitas
EJEMPLO 1
Encuentra la suma infinita de la siguiente progresión geométrica:
$$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+…$$
Solución
Empezamos escribiendo la información que conocemos:
- Primer término: $latex a=1$
- Razón común: $latex r=\frac{1}{2}$
Ahora, usamos la fórmula de la suma infinita de una progresión geométrica:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{1}{1-\frac{1}{2}}$$
$$=\frac{1}{\frac{1}{2}}$$
$latex S_{\infty}=2$
EJEMPLO 2
Encuentra la suma infinita de una progresión geométrica en la que el primer término es igual a -3 y la razón común es igual a $latex -\frac{1}{2}$.
Solución
En este caso, tenemos los siguientes valores
- Primer término: $latex a=-3$
- Razón común: $latex r=-\frac{1}{2}$
Al aplicar la fórmula de la suma infinita de una progresión geométrica, tenemos:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{-3}{1+\frac{1}{2}}$$
$$=\frac{-3}{\frac{3}{2}}$$
$latex S_{\infty}=-2$
EJEMPLO 3
Encuentra la suma infinita de la siguiente progresión geométrica:
$$2+\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+…$$
Solución
En este caso, tenemos lo siguiente
- Primer término: $latex a=2$
- Razón común: $latex r=\frac{1}{4}$
Cuando usamos la fórmula de la suma infinita, tenemos:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{2}{1-\frac{1}{4}}$$
$$=\frac{2}{\frac{3}{4}}$$
$$S_{\infty}=\frac{8}{3}$$
EJEMPLO 4
Encuentra el resultado de la siguiente suma:
$$\sum_{r=1}^{\infty}\left(\frac{1}{5}\right)^r$$
Solución
Aquí, tenemos a la suma de la progresión geométrica escrita en forma de sumatoria. Encontramos el valor del primer término al usar $latex r=1$.
La razón común es el número dentro del paréntesis, por lo que tenemos:
- Primer término: $latex a=\frac{1}{5}$
- Razón común: $latex r=\frac{1}{5}$
Usando la fórmula de la suma infinita con estos valores, tenemos:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{1}{5}}{1-\frac{1}{5}}$$
$$=\frac{\frac{1}{5}}{\frac{4}{5}}$$
$$=\frac{5}{20}$$
$$S_{\infty}=\frac{1}{4}$$
EJEMPLO 5
Escribe al decimal recurrente 0.3232… como la suma de una progresión geométrica y luego, escribe al decimal como un número racional.
Solución
Para resolver este ejercicio, empezamos escribiendo al decimal como la suma de una progresión geométrica:
$$0.323232…= \frac{32}{100}+\frac{32}{10000}+\frac{32}{1000000}+…$$
Ahora, identificamos los siguientes valores:
- $latex a=\frac{32}{100}$
- $latex r=\frac{1}{100}$
Dado que $latex -1<r<1$, podemos calcular el valor de la suma infinita:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{32}{100}}{1-\frac{1}{100}}$$
$$=\frac{\frac{32}{100}}{\frac{99}{100}}$$
$$S_{\infty}=\frac{32}{99}$$
Entonces, el decimal recurrente 0.3232…, puede ser escrito como $latex \frac{32}{99}$.
EJEMPLO 6
Expresa al decimal recurrente 0.7272… como una fracción en su forma más imple.
Solución
Escribimos al decimal como una progresión geométrica:
$$0.727272…= \frac{72}{100}+\frac{72}{10000}+\frac{72}{1000000}+…$$
Ahora, podemos observar que la progresión tiene los siguientes valores:
- $latex a=\frac{72}{100}$
- $latex r=\frac{1}{100}$
Dado que $latex -1<r<1$, podemos calcular el valor de la suma infinita:
$$S_{\infty}=\frac{a}{1-r}$$
$$=\frac{\frac{72}{100}}{1-\frac{1}{100}}$$
$$=\frac{\frac{72}{100}}{\frac{99}{100}}$$
$$=\frac{72}{99}$$
$$S_{\infty}=\frac{8}{11}$$
Entonces, el decimal recurrente 0.7272…, puede ser escrito como $latex \frac{8}{11}$.
Suma de progresiones geométricas infinitas – Ejercicios para resolver
Encuentra la suma infinita de la siguiente progresión geométrica $$4+\frac{4}{3}+\frac{4}{9}+…$$
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre progresiones geométricas? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
