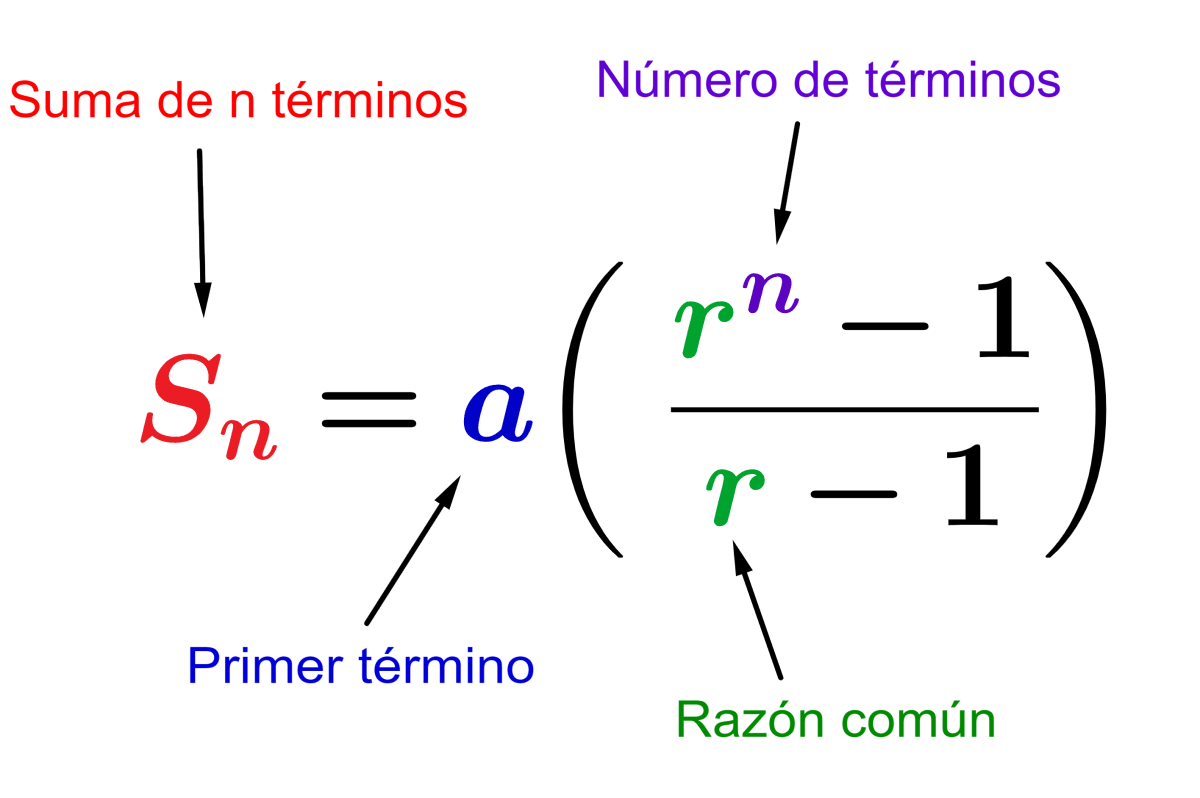
La suma de cualquier progresión geométrica puede ser calculada usando una fórmula estándar. Esta fórmula usa los valores del primer término, la razón común y el número de términos. Existen dos variaciones de esta fórmula que pueden ser aplicadas dependiendo de si la razón común es mayor que 1 o menor que 1.
A continuación, resolveremos algunos ejercicios de suma de progresiones geométricas. Además, veremos algunos ejercicios de práctica para aplicar lo aprendido.
ÁLGEBRA
Relevante para…
Resolver algunos ejercicios de suma de progresiones geométricas.
ÁLGEBRA
Relevante para…
Resolver algunos ejercicios de suma de progresiones geométricas.
Fórmulas para la suma de una progresión geométrica
Una progresión geométrica es una progresión en la que cada uno de sus términos es formado al multiplicar al término anterior por un número llamado la razón común.
Podemos encontrar la suma de los primeros $latex n$ términos de una progresión geométrica usando la siguiente fórmula:
$$S_{n}=a\left( \frac{1-r^n}{1-r}\right)$$
Alternativamente, podemos escribir a la fórmula de la siguiente forma:
$$S_{n}=a\left( \frac{r^n-1}{r-1}\right)$$
en donde,
- $latex a$ es el primer término de la progresión.
- $latex r$ es la razón común.
- $latex n $ es el número de términos.
Demostración de la fórmula de la suma de progresiones geométricas
Cada término de una progresión geométrica es obtenido al multiplicar al término anterior por la razón común $latex r$. Entonces, podemos escribir lo siguiente:
$$S_{n}=a+ar+ar^2+…+ar^{n-1}$$
Esta es la ecuación [1]. Si es que multiplicamos a ambos lados de la ecuación por $latex r$, tenemos:
$$rS_{n}=ar+ar^2+ar^3+…+ar^n$$
Esta es la ecuación [2]. Si es que restamos a ecuación [2] de la ecuación [1], tenemos:
$$S_{n}-rS_{n}=(a+ar+…+ar^{n-1})-(ar+ar^2+…+ar^n)$$
Simplificando, tenemos:
$$S_{n}(1-r)=a-ar^n$$
$$S_{n}=\frac{a(1-r^n)}{1-r}$$
Podemos obtener la versión alternativa si es que multiplicamos tanto al numerador, como al denominador de esta fórmula por -1:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
10 Ejercicios resueltos de sumas de progresiones geométricas
EJERCICIO 1
¿Cuál es la suma de los primeros cuatro términos de una progresión geométrica en la que el primer término es igual a 5 y la razón común es igual a 2?
Solución
Para resolver este ejercicio, empezamos escribiendo la información que conocemos:
- Primer término: $latex a=5$
- Razón común: $latex r=2$
- Número de términos: $latex n=4$
Ahora, podemos usar la fórmula de la suma de una progresión geométrica con los valores dados:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{4}=\frac{5(2^4-1)}{2-1}$$
$$=\frac{5(16-1)}{1}$$
$$=\frac{5(15)}{1}$$
$$S_{4}=75$$
EJERCICIO 2
Si es que una progresión geométrica empieza con el término 6 y su razón común es -2, encuentra la suma de los primeros 5 términos.
Solución
Empezamos escribiendo la información que conocemos:
- Primer término: $latex a=6$
- Razón común: $latex r=-2$
- Número de términos: $latex n=5$
Aplicando la fórmula de la suma de progresiones geométricas, tenemos:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{5}=\frac{6((-2)^5-1)}{-2-1}$$
$$=\frac{6(-32-1)}{-3}$$
$$=\frac{6(-33)}{-3}$$
$$=\frac{-198}{-3}$$
$latex S_{5}=66$
EJERCICIO 3
Encuentra la suma de los primeros cuatro términos de una progresión geométrica que tiene un primer término igual a 1 y una razón común igual a $latex \frac{1}{4}$.
Solución
Tenemos los siguientes valores:
- Primer término: $latex a=1$
- Razón común: $latex r=\frac{1}{4}$
- Número de términos: $latex n=4$
Al aplicar la fórmula de la suma de progresiones geométricas, tenemos:
$$S_{n}=\frac{a(1-r^n)}{1-r}$$
$$S_{4}=\frac{1(1-(\frac{1}{4})^4)}{1-\frac{1}{4}}$$
Vamos a aplicar la diferencia de cuadrados en el numerador dos veces. Luego, simplificamos:
$$S_{4}=\frac{(1-(\frac{1}{4})^2)(1+(\frac{1}{4})^2)}{1-\frac{1}{4}}$$
$$=\frac{(1-\frac{1}{4})(1+\frac{1}{4})(1+(\frac{1}{4})^2)}{1-\frac{1}{4}}$$
$$=\left(1+\frac{1}{4}\right)\left(1+(\frac{1}{4})^2\right)$$
$$=\left(\frac{5}{4}\right)\left(\frac{17}{16}\right)$$
$$S_{4}=\frac{85}{64}$$
EJERCICIO 4
Una progresión geométrica empieza con los términos 3, 6, 12, … Encuentra la suma de los primeros 10 términos.
Solución
No conocemos el valor de la razón común directamente, pero podemos encontrarlo al dividir a un término por su término previo. Entonces, tenemos: 6/3=2:
- $latex a=3$
- $latex r=2$
- $latex n=10$
Cuando usamos estos valores en la fórmula de la suma, tenemos:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{10}=\frac{3(2^{10}-1)}{2-1}$$
$$=\frac{3(1024-1)}{1}$$
$latex =3(1023)$
$latex S_{10}=3069$
EJERCICIO 5
Encuentra la suma de los primeros 8 términos de una progresión geométrica que empieza con los términos 5, 10, 20, …
Solución
Para resolver este ejercicio, tenemos que empezar encontrando la razón común. Entonces, tenemos: 10/5=2, por lo que tenemos los siguientes valores:
- $latex a=5$
- $latex r=2$
- $latex n=8$
Ahora, usamos estos valores en la fórmula de la suma:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{8}=\frac{5(2^8-1)}{2-1}$$
$$=\frac{5(256-1)}{1}$$
$latex =5(255)$
$latex S_{8}=1275$
EJERCICIO 6
¿Cuál es la suma de los primeros 6 términos de la progresión geométrica que empieza con los términos -2, 8, -32, …?
Solución
Similar a los ejercicios anteriores, empezamos encontrando la razón común. Entonces, 8/-2=-4, por lo que tenemos lo siguiente:
- $latex a=-2$
- $latex r=-4$
- $latex n=6$
Cuando usamos la fórmula de la suma de progresiones geométricas, tenemos:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{6}=\frac{-2((-4)^6-1)}{-4-1}$$
$$=\frac{-2(4096-1)}{-5}$$
$$=\frac{-2(4095)}{-5}$$
$latex S_{6}=1638$
EJERCICIO 7
Encuentra la suma de los primeros 7 términos de una progresión geométrica que empieza con los términos $latex 1, ~\frac{1}{3},~\frac{1}{9}$.
Solución
La razón común de la progresión es $latex \frac{1}{3} \div 1= \frac{1}{3}$. Entonces, tenemos lo siguiente:
- $latex a=1$
- $latex r=\frac{1}{3}$
- $latex n=7$
Ahora, usamos la fórmula de la suma en su versión alternativa, ya que la razón común es menor que 1 y tenemos:
$$S_{n}=\frac{a(1-r^n)}{1-r}$$
$$S_{7}=\frac{1(1-(\frac{1}{3})^7}{1-\frac{1}{3}}$$
$$=\frac{(1-\frac{1}{2187})}{\frac{2}{3}}$$
$$=\frac{\frac{2186}{2187}}{\frac{2}{3}}$$
$$=\frac{1093}{729}$$
$latex S_{7}=1~ \frac{364}{729}$
EJERCICIO 8
¿Cuál es la suma de la siguiente progresión geométrica?
$$3+6+12+…+384$$
Solución
En este caso, conocemos los tres primeros términos y el último término. No conocemos ni la razón común, ni el número de términos.
La razón común es 6/3=2. Para encontrar el número de términos, usamos la fórmula del término general de una progresión geométrica, $latex a_{n}=ar^{n-1}$ y resolvemos para $latex n$:
$latex a_{n}=ar^{n-1}$
$latex 384=(3)(2)^{n-1}$
$latex 128=2^{n-1}$
$$128=\frac{2^n}{2^1}$$
$latex 256=2^n$
$latex n=\log_{2}(256)$
$latex n=8$
Ahora que tenemos todos los valores requeridos, usamos la fórmula de la suma:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{8}=\frac{3(2^8-1)}{2-1}$$
$$=\frac{3(256-1)}{1}$$
$latex =3(255)$
$latex S_{8}=765$
EJERCICIO 9
Encuentra la suma de la siguiente progresión geométrica:
$$4-12+36-…-972$$
Solución
Nuevamente, empezamos encontrando la razón común: -12/4=-3.
Ahora, usamos la fórmula del término general de una progresión geométrica, $latex a_{n}=ar^{n-1}$ para encontrar el número de términos:
$latex a_{n}=ar^{n-1}$
$latex -972=(4)(-3)^{n-1}$
$latex 243=(-3)^{n-1}$
$$243=\frac{(-3)^n}{(-3)^1}$$
$latex -729=(-3)^n$
$latex n=6$
Aplicando la fórmula de la suma con los valores encontrados, tenemos:
$$S_{n}=\frac{a(r^n-1)}{r-1}$$
$$S_{6}=\frac{4((-3)^6-1)}{(-3)-1}$$
$$=\frac{4(729-1)}{-4}$$
$latex S_{6}=-728$
EJERCICIO 10
Encuentra la suma de la siguiente progresión geométrica:
$$\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+…+\frac{1}{4096}$$
Solución
Empezamos encontrando la razón común de la progresión: $latex \frac{1}{16}\div \frac{1}{4}=\frac{1}{4}$.
Ahora, encontramos el número de términos usando la fórmula $latex a_{n}=ar^{n-1}$:
$latex a_{n}=ar^{n-1}$
$$\frac{1}{4096}=\left(\frac{1}{4}\right)\left(\frac{1}{4}\right)^{n-1}$$
$$\frac{1}{1024}=\left(\frac{1}{4}\right)^{n-1}$$
$$\frac{1}{1024}=\frac{\left(\frac{1}{4}\right)^n}{\left(\frac{1}{4}\right)^1}$$
$latex 4^n=4096$
$latex n=\log_{4}(4096)$
$latex n=6$
Aplicando la fórmula de la suma con estos valores, tenemos:
$$S_{6}=\frac{\frac{1}{4}\left(1-\left(\frac{1}{4}\right)^6\right)}{1-\frac{1}{4}}$$
$$=\frac{\frac{1}{4}\left(1-\frac{1}{4096}\right)}{\frac{3}{4}}$$
$$=\frac{\frac{1}{4}\left(\frac{4095}{4096}\right)}{\frac{3}{4}}$$
$$S_{6}=\frac{1365}{4096}$$
Ejercicios de suma de progresiones geométricas para resolver
Encuentra la suma de la siguiente progresión geométrica $$7-14+28-…+448$$
Escribe la respuesta en la casilla.
Véase también
¿Interesado en aprender más sobre progresiones geométricas? Puedes mirar estas páginas: