La recta tangente a una curva es encontrada usando la forma y=mx+b, en donde m es la pendiente de la recta y b es el intercepto en y. A su vez, la pendiente es calculada usando la derivada de la función. De igual forma, encontramos la ecuación de la recta normal considerando que su pendiente es un recíproco negativo de la recta tangente.
A continuación, aprenderemos sobre las rectas tangente y normal a una curva. Conoceremos cómo obtener sus ecuaciones y resolveremos algunos ejemplos de práctica.
CÁLCULO
Relevante para…
Aprender a encontrar la ecuación de la recta tangente a una curva.
CÁLCULO
Relevante para…
Aprender a encontrar las ecuaciones de las rectas tangente y normal a una curva.
¿Cómo encontrar la ecuación de la recta tangente a una curva?
La ecuación de la recta tangente a una curva puede ser encontrada si es que conocemos la función que produce la curva y las coordenadas del punto tangencial, como podemos ver en el siguiente diagrama:
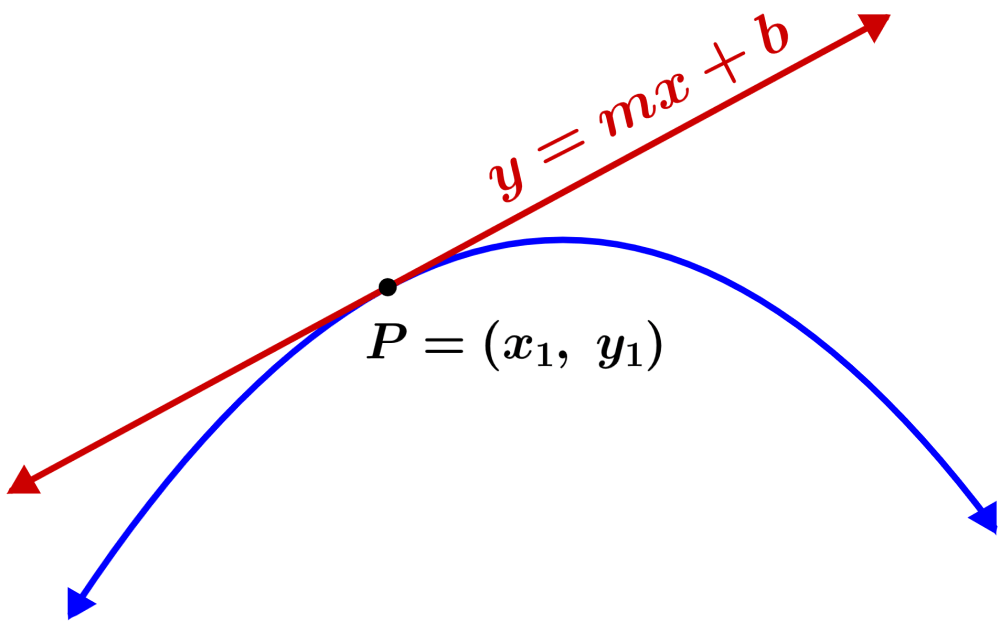
Entonces, podemos usar la forma pendiente-intercepto de una función lineal, $latex y=mx+b$, en donde m es la pendiente de la recta y b es el intercepto en y.
Si es que conocemos la función que produce la curva y las coordenadas del punto $latex P=(x_{1},~y_{1})$, podemos seguir los siguientes pasos:
Paso 1: Obtener la derivada de la función que produce la curva.
Paso 2: Determinar la pendiente de la recta tangente usando la derivada.
Dado que conocemos el punto tangencial $latex (x_{1},~y_{1})$, podemos evaluar la derivada de la función en la coordenada x del punto para obtener la pendiente. Es decir, tenemos $latex m=f'(x_{1})$.
Paso 3: Encontrar el valor de b usando la ecuación $latex y=mx+b$ con el valor de la pendiente encontrada en el paso 2.
Podemos lograr esto al usar las coordenadas $latex (x_{1},~y_{1})$ del punto dado en la forma $latex y=mx+b$ y resolver para b. Es decir, tenemos $latex y_{1}=mx_{1}=b$.
Paso 4: Usar los valores de m y b en la forma $latex y=mx+b$ para obtener la ecuación de la recta tangente.
¿Cómo encontrar la ecuación de la recta normal a una curva?
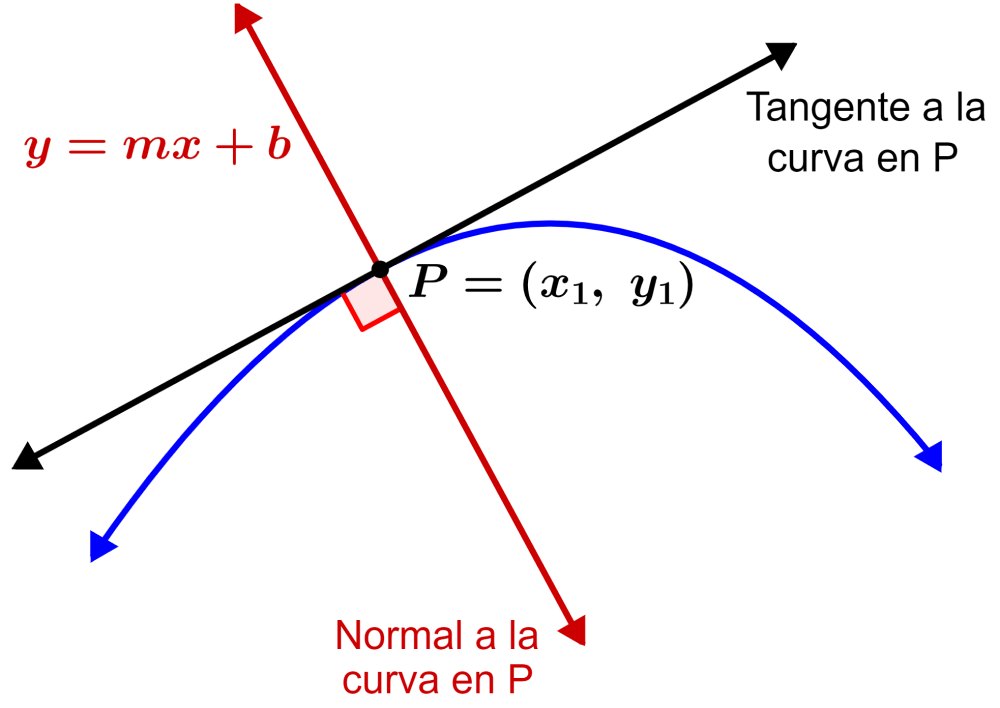
La ecuación de la recta normal a una curva es encontrada en una forma similar a como encontramos la ecuación de la recta tangente. La diferencia es que consideramos que la recta normal es perpendicular a la recta tangente, como se muestra en el diagrama:
Entonces, la pendiente de la recta normal es igual al recíproco negativo de la recta tangente. Es decir, si es que la pendiente de la tangente es $latex m$, entonces la pendiente de la normal es igual a $latex -\frac{1}{m}$.
Si es que conocemos la función que representa a la curva y las coordenadas del punto $latex (x_{1},~y_{1})$, podemos seguir los siguientes pasos:
Paso 1: Determinar la derivada de la función.
Paso 2: Usar la derivada para encontrar la pendiente de la recta tangente a la curva en el punto $latex (x_{1},~y_{1})$. Para esto, tenemos $latex m_{1}=f'(x_{1})$.
Paso 3: Determinar la pendiente de la recta normal usando la pendiente del paso 2. La pendiente de la recta normal es igual a $latex m=-\frac{1}{m_{1}}$, en donde $latex m_{1}$ es la pendiente de la recta tangente.
Paso 4: Usando la forma $latex y=mx+b$ y la pendiente del paso 3, determinados el valor de b. Para esto, usamos las coordenadas del punto $latex (x_{1},~y_{1})$. Es decir, tenemos $latex y_{1}=mx_{1}=b$.
Paso 5: Sustituimos los valores de m y b en la forma $latex y=mx+b$ para obtener la ecuación de la recta normal.
Ejemplos de la recta tangente y la recta normal a una curva
EJEMPLO 1
Si tenemos la función $latex f(x)=3x^2-3x$, encuentra la ecuación de la recta tangente en el punto (1, 3).
Solución
Paso 1: Empezamos encontrando la derivada de la función que representa a la curva:
$latex f(x)=3x^2-3x$
$latex f'(x)=6x-3$
Paso 2: Evaluamos $latex f'(1)$ para encontrar la pendiente de la recta tangente en el punto (1, 3):
$latex m=f'(1)=6(1)-3$
$latex m=3$
Paso 3: La pendiente del paso 2 nos da la ecuación $latex y=3x+b$. Entonces, usamos el punto (1, 3) en la ecuación para encontrar el valor de b:
$latex y=3x+b$
$latex 3=3(1)+b$
$latex b=0$
Paso 4: La ecuación de la recta tangente en el punto (1, 3) es $latex y=3x$.
EJEMPLO 2
Tenemos la función $latex f(x)=x^2$. Determina la ecuación de la recta normal en el punto P=(3, 2).
Solución
Paso 1: La derivada de la función es:
$latex f(x)=x^2$
$latex f'(x)=2x$
Paso 2: Evaluamos $latex f'(3)$ para encontrar la pendiente de la recta tangente en el punto (3, 2). Entonces, tenemos:
$latex m_{1}=f'(3)=2(3)$
$latex m_{1}=6$
Paso 3: Usamos la pendiente de la recta tangente para encontrar la pendiente de la recta normal, la cual es $latex m=-\frac{1}{6}$.
Paso 4: Usando la pendiente de la normal, tenemos la ecuación $latex y=-\frac{1}{6}x+b$. Ahora, usamos el punto (3, 2) en la ecuación para determinar el valor de b:
$latex y=-\frac{1}{6}x+b$
$latex 2=-\frac{1}{6}(3)+b$
$latex b=\frac{5}{2}$
Paso 5: La ecuación de la recta normal en el punto (3, 2) es $latex y=-\frac{1}{6}x+\frac{5}{2}$.
EJEMPLO 3
¿Cuál es la ecuación de la recta tangente a la función $latex f(x) = -x^{-2}+\sqrt{x}$ en el punto (1, 3)?
Solución
Paso 1: Para encontrar la derivada, usamos las leyes de los exponentes para escribir a la raíz cuadrada como un exponente numérico:
$latex f(x)=-x^{-2}+x^{\frac{1}{2}}$
$$f'(x)=2x^{-3}+\frac{1}{2}x^{-\frac{1}{2}}$$
$$f'(x)=\frac{2}{x^3}+\frac{1}{2\sqrt{x}}$$
Paso 2: Usando la derivada, evaluamos $latex f'(1)$ para encontrar la pendiente de la recta tangente en (1, 3):
$$m=f'(1)=\frac{2}{(1)^3}+\frac{1}{2\sqrt{1}}$$
$latex =2+\frac{1}{2}$
$latex m=\frac{5}{2}$
Paso 3: La pendiente del paso 2 nos da la ecuación $latex y=\frac{5}{2}x+b$. Entonces, usamos el punto (1, 3) en la ecuación para encontrar el valor de b:
$$y=\frac{5}{2}x+b$$
$$3=\frac{5}{2}(1)+b$$
$latex b=\frac{1}{2}$
Paso 4: La ecuación de la recta tangente en el punto (1, 3) es $latex y=\frac{5}{2}x+\frac{1}{2}$.
EJEMPLO 4
Si tenemos la función $latex f(x)=x^3+\frac{8}{x}$, determina la ecuación de la recta normal en el punto (2, -2).
Solución
Paso 1: Usamos las leyes de los exponentes para escribir a la función solo con exponentes numéricos y así, calcular su derivada:
$latex f(x)=x^3+8x^{-1}$
$latex f'(x)=x^2-8x^{-2}$
$latex f'(x)=x^2-\frac{8}{x^2}$
Paso 2: La pendiente de la tangente en (2, 4) es encontrada al evaluar $latex f'(2)$:
$latex m_{1}=f'(2)=(2)^2-\frac{8}{2^2}$
$latex =4-2$
$latex m_{1}=2$
Paso 3: Usamos la pendiente del paso 2 para determinar la pendiente de la normal y tenemos $latex m=-\frac{1}{2}$.
Paso 4: Con la pendiente del paso 3, tenemos la ecuación $latex y=-\frac{1}{2}x+b$. Ahora, usamos el punto (2, -2) en la ecuación para encontrar el valor de b,:
$latex y=-\frac{1}{2}x+b$
$latex -2=-\frac{1}{2}(2)+b$
$latex b=-1$
Paso 5: La ecuación de la recta normal en el punto (2, 4) es $latex y=-\frac{1}{2}x-1$.
EJEMPLO 5
Si es que tenemos la función $latex f(x)=x^2-3x+1$, encuentra la ecuación de la recta tangente en el punto en donde la curva corta al eje y.
Solución
Paso 1: La derivada de la función es:
$latex f(x)=x^2-3x+1$
$latex f'(x)=2x-3$
Paso 2: No tenemos las coordenadas del punto tangencial, pero sabemos que la recta es tangente en el punto donde la curva corta al eje y.
Cuando una función corta al eje y, las coordenadas en x son igual a 0. Entonces, tenemos:
$latex y=x^2-3x+1$
$latex y=0^2-3(0)+1$
$latex y=1$
Entonces el punto es (0, 1). Ahora, evaluamos $latex f'(0)$ para encontrar la pendiente de la tangente y tenemos:
$latex m=f'(0)=2(0)-3$
$latex m=-3$
Paso 3: Con la pendiente del paso 3, tenemos la ecuación $latex y=-3x+b$. Entonces, usamos el punto (0, 1) en la ecuación para encontrar el valor de b:
$latex y=-3x+b$
$latex 1=-3(0)+b$
$latex b=1$
Paso 4: La ecuación de la recta tangente en el punto (0, 1) es $latex y=-3x+1$.
EJEMPLO 6
Encuentra la recta normal a la función $latex f(x)=\sin(x)-\cos(x)$ en el punto (0, 1).
Solución
Paso 1: La derivada de la función trigonométrica dada es:
$latex f(x)=\sin(x)-\cos(x)$
$latex f'(x)=\cos(x)+\sin(x)$
Paso 2: Evaluamos $latex f'(0)$ para encontrar la pendiente de la recta tangente en el punto (0, 1):
$latex m=f'(0)=\cos(0)+\sin(0)$
$latex m_{1}=1+0$
$latex m_{1}=1$
Paso 3: La pendiente de la recta normal es igual a $latex m=-1$.
Paso 4: Con la pendiente del paso 3, tenemos la ecuación $latex y=-x+b$. Entonces, usamos el punto (0, 1) en la ecuación para encontrar el valor de b:
$latex y=-x+b$
$latex 1=-0+b$
$latex b=1$
Paso 5: La ecuación de la recta normal en el punto (0, 1) es $latex y=-x+1$.
Recta tangente y recta normal a una curva – Ejercicios para resolver
Véase también
¿Interesado en aprender más sobre ecuaciones de rectas tangentes y normales a funciones? Puedes mirar estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
