El teorema de Tales nos dice que, un triángulo inscrito en un círculo, en donde, la hipotenusa corresponde al diámetro del círculo, siempre es un triángulo rectángulo. Este teorema puede ser demostrado usando la suma de ángulos interiores.
A continuación, veremos un resumen del teorema de Tales. Luego, aprenderemos a aplicar este teorema para resolver algunos ejercicios de práctica.
Resumen del teorema de Tales
El teorema de Tales es considerado como un caso especial del teorema de ángulos inscritos. Este teorema nos dice que, si es que tenemos a un triángulo inscrito en un círculo como se muestra en el siguiente diagrama, el ángulo formado en el vértice B siempre es un ángulo recto.
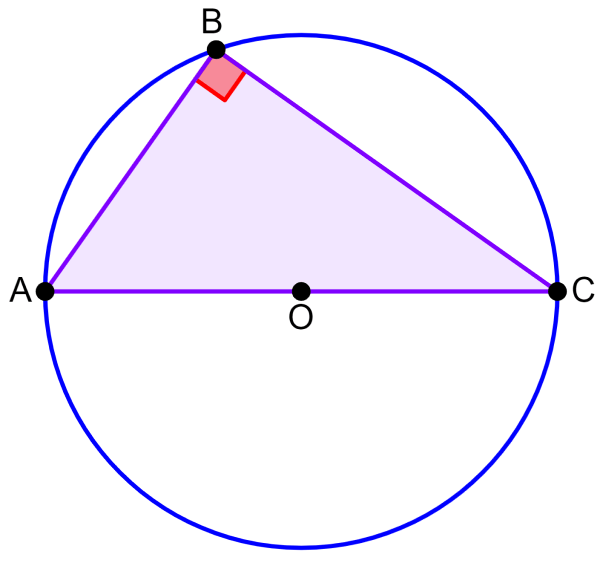
Entonces, si es que tres puntos A, B y C se ubican en la circunferencia de un círculo, en donde, la línea AC es el diámetro del círculo, entonces, el ángulo ∠ABC es un ángulo recto (90°).
Este teorema puede ser demostrado al trazar un bisector desde el centro hasta el vértice B y luego usar los ángulos de los triángulos isósceles formados y el hecho que la suma de ángulos internos de cualquier triángulo es igual a 180°. Puedes mirar la demostración completa en este artículo.
Ejercicios del teorema de Tales resueltos
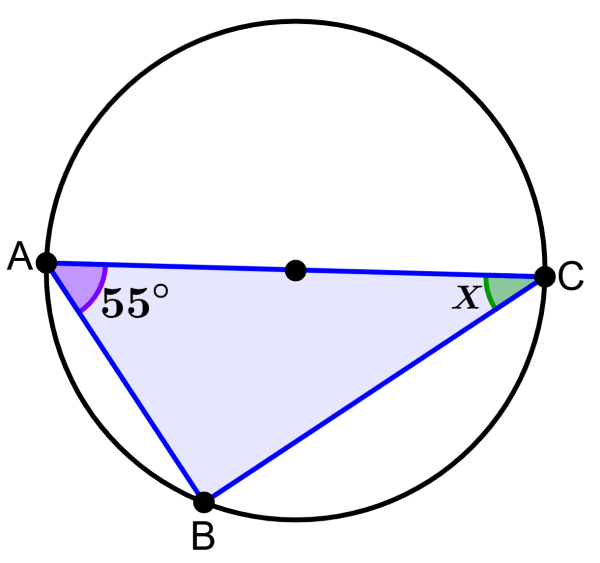
EJERCICIO 1
El segmento AC es el diámetro del círculo. ¿Cuál es la medida del ángulo Z?
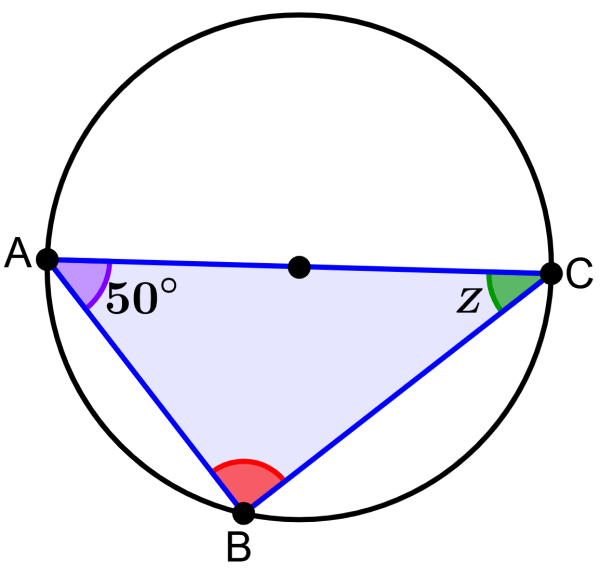
Solución
El segmento AC es el diámetro del círculo, por lo que podemos usar el teorema de Tales. Entonces, sabemos que el ángulo en el vértice B es un ángulo de 90°. Dado que la suma de ángulos internos en cualquier triángulo es igual a 180°, tenemos:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
La medida del ángulo Z es 40°.
EJERCICIO 2
Determina la medida del ángulo Z en el siguiente diagrama si es que el segmento AC es el diámetro del círculo.
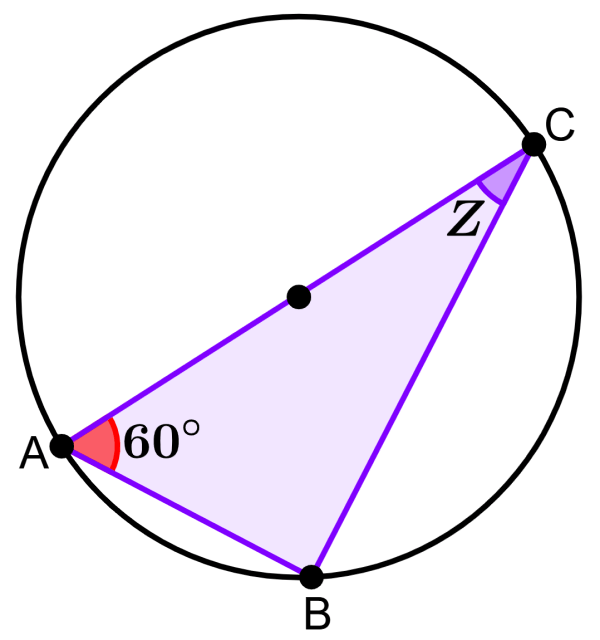
Solución
El segmento AC es el diámetro del círculo, por lo que podemos usar el teorema de Tales. Entonces, sabemos que el ángulo en el vértice B es un ángulo de 90°. Dado que la suma de ángulos internos en cualquier triángulo es igual a 180°, tenemos:
90°+60°+Z=180°
150°+Z=180°
Z=180°-150°
Z=30°
La medida del ángulo Z es 30°.
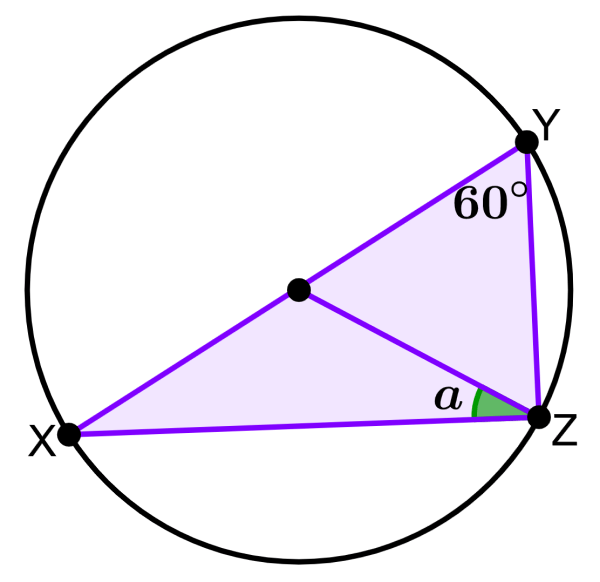
EJERCICIO 3
Si es que M es el centro del círculo, determina la medida del ángulo Z.
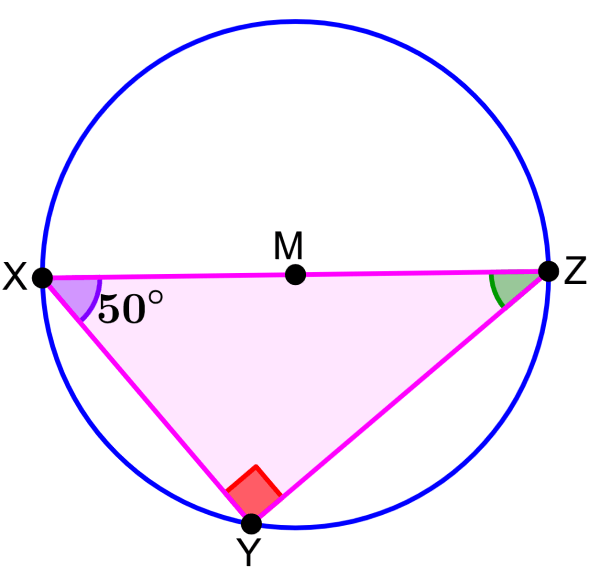
Solución
Dado que el punto M es el centro del círculo, sabemos que el segmento XZ es el diámetro del círculo. Entonces, sí podemos usar el teorema de Tales.
Por el teorema, sabemos que el ángulo en el vértice Y es un ángulo de recto, es decir, un ángulo de 90°. Podemos usar la suma de ángulos internos de un triángulo para obtener la medida de Z:
90°+50°+Z=180°
140°+Z=180°
Z=180°-140°
Z=40°
La medida del ángulo Z es 40°.
EJERCICIO 4
Si es que O representa al centro del círculo, cuál es la medida del ángulo a?
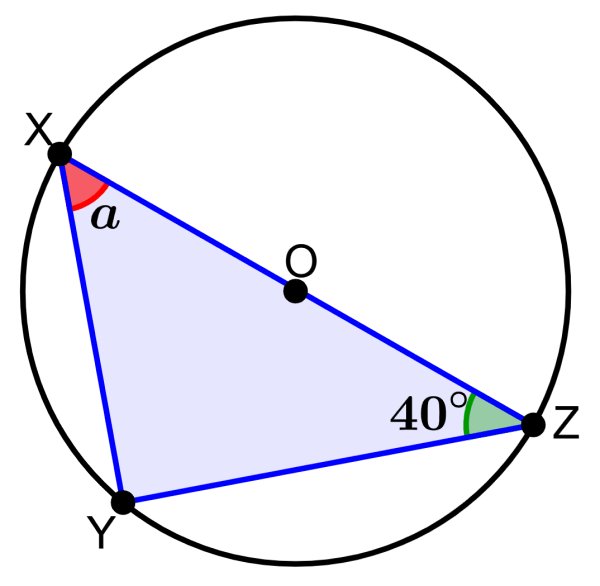
Solución
Si el que el punto O es el centro del círculo, sabemos que el segmento XZ representa al diámetro del círculo. Entonces, podemos aplicar el teorema de Tales. Usando el teorema, sabemos que el ángulo Y es recto, es decir, de 90°.
Ahora, usamos la suma de ángulos internos de un triángulo para encontrar la medida del ángulo a:
90°+40°+a=180°
130°+a=180°
a=180°-130°
a=50°
La medida del ángulo a es 50°.
EJERCICIO 5
El segmento AC es un diámetro del círculo. ¿Cuál es la medida del diámetro?
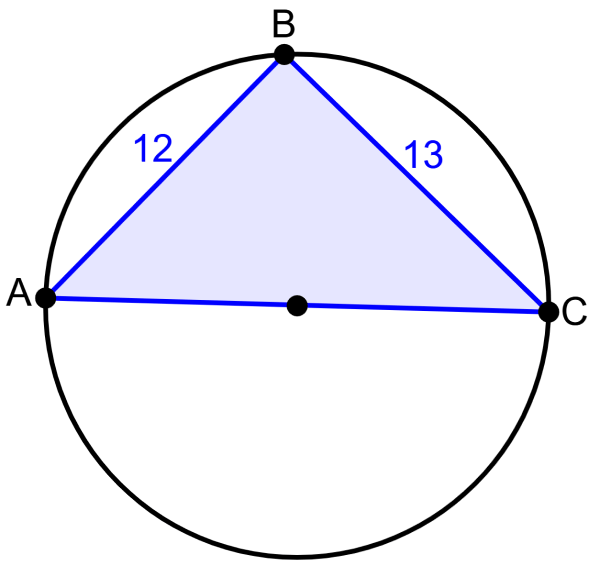
Solución
Usando el teorema de Tales, podemos determinar que el triángulo ABC es un triángulo rectángulo. Esto significa que el ángulo B es un ángulo recto. Entonces, podemos usar el teorema de Pitágoras para encontrar la longitud del diámetro:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{12}^2}+{{13}^2}$
$latex {{c}^2}=144+169$
$latex {{c}^2}=313$
$latex c=17.7$
La longitud del segmento AC es 17.7 unidades.
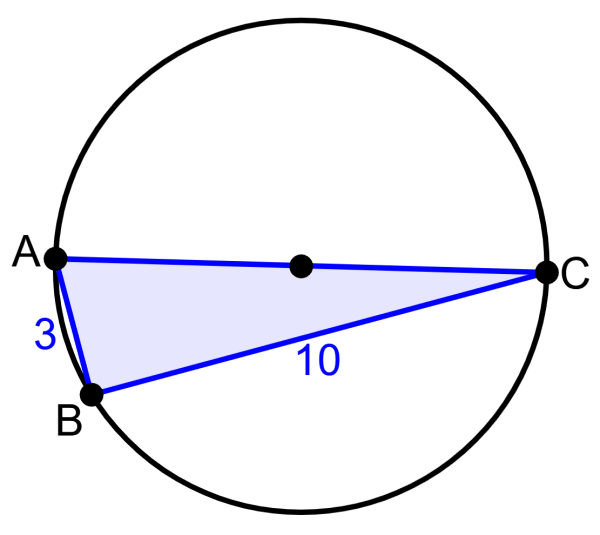
EJERCICIO 6
Determina la longitud del segmento AB en el siguiente diagrama.
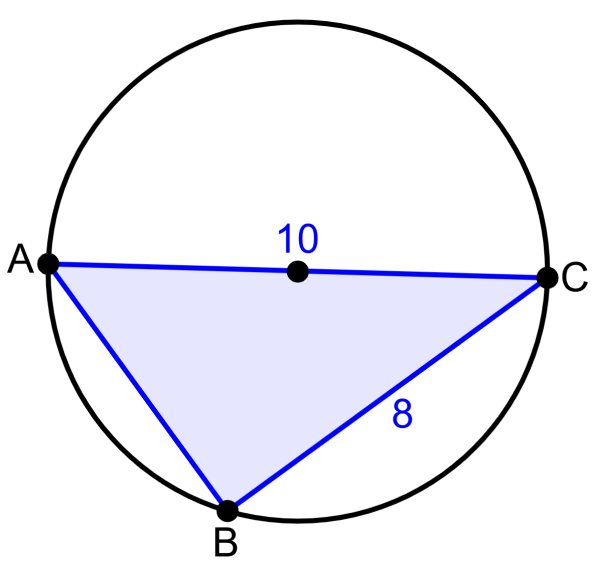
Solución
El segmento AC es el diámetro del círculo. Entonces, aplicando el teorema de Tales, podemos determinar que el triángulo ABC es un triángulo rectángulo.
Por lo tanto, usamos el teorema de Pitágoras para encontrar la longitud del segmento AB:
$latex {{a}^2}+{{b}^2}={{c}^2}$
$latex {{a}^2}+{{8}^2}={{10}^2}$
$latex {{a}^2}+64=100$
$latex {{a}^2}=100-64$
$latex {{a}^2}=36$
$latex a=6$
La longitud del segmento AB es 6 unidades.
EJERCICIO 7
Si es que el segmento XY es el diámetro del círculo, ¿cuál es su longitud?
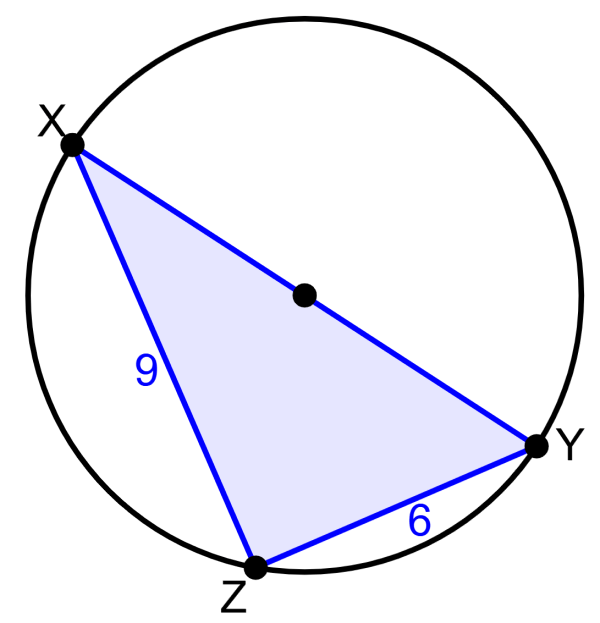
Solución
Al aplicar el teorema de Tales, encontramos que el triángulo XYZ es un triángulo rectángulo. Es decir, el ángulo Z es un ángulo recto.
Entonces, encontramos la longitud de XY al aplicar el teorema de Pitágoras, en donde, XY es la hipotenusa de un triángulo rectángulo:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{6}^2}+{{9}^2}$
$latex {{c}^2}=36+81$
$latex {{c}^2}=117$
$latex c=10.82$
La longitud del segmento XY es 10.82 unidades.
EJERCICIO 8
¿Cuál es la longitud de AC si es que AB es el diámetro del círculo?
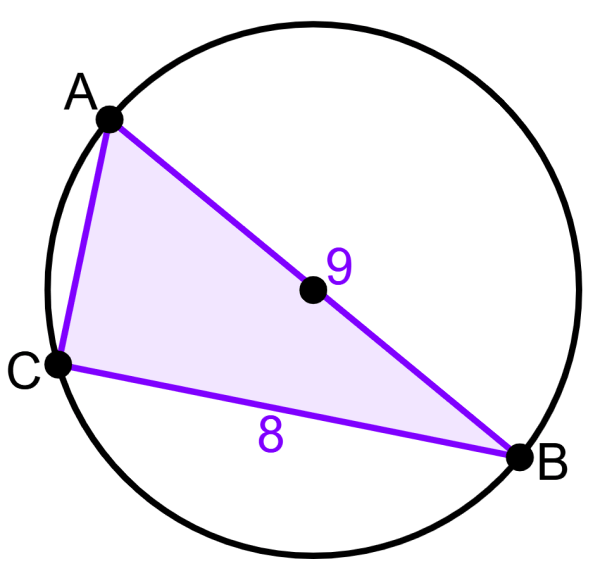
Solución
Dado que AB es el diámetro del círculo, sabemos que el teorema de Tales aplica. Esto significa que el triángulo es un triángulo rectángulo y podemos usar el teorema de Pitágoras para encontrar la longitud del segmento AC:
$latex {{a}^2}+{{b}^2}={{c}^2}$
$latex {{a}^2}+{{8}^2}={{9}^2}$
$latex {{a}^2}+64=81$
$latex {{a}^2}=81-64$
$latex {{a}^2}=17$
$latex a=4.12$
La longitud del segmento AC es 4.12 unidades.
EJERCICIO 9
Si es que C es el centro del círculo, ¿cuál es la medida del ángulo ∠ABC?
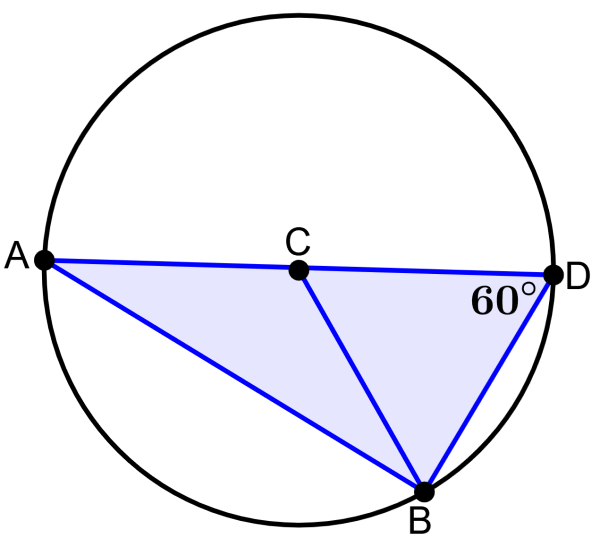
Solución
Dado que el punto C es el centro del círculo, sabemos que el segmento AD es el diámetro. Entonces, podemos aplicar el teorema de Tales.
Dos de los lados de los triángulos ABC y BCD son iguales, ya que corresponden a los radios del círculo. Entonces, dos ángulos también son iguales y los triángulos deben ser triángulos isósceles. Entonces, tenemos:
∠CBD = ∠CDB =60°
Aplicando el teorema de Tales, tenemos:
∠ABD =90°
Entonces, tenemos:
∠ABC = 90°-60°=30°
Por lo tanto, la medida del ángulo ∠ABC es 30°.
Ejercicios de teorema de Tales para resolver
Véase también
¿Interesado en aprender más sobre el teorema de Tales? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
