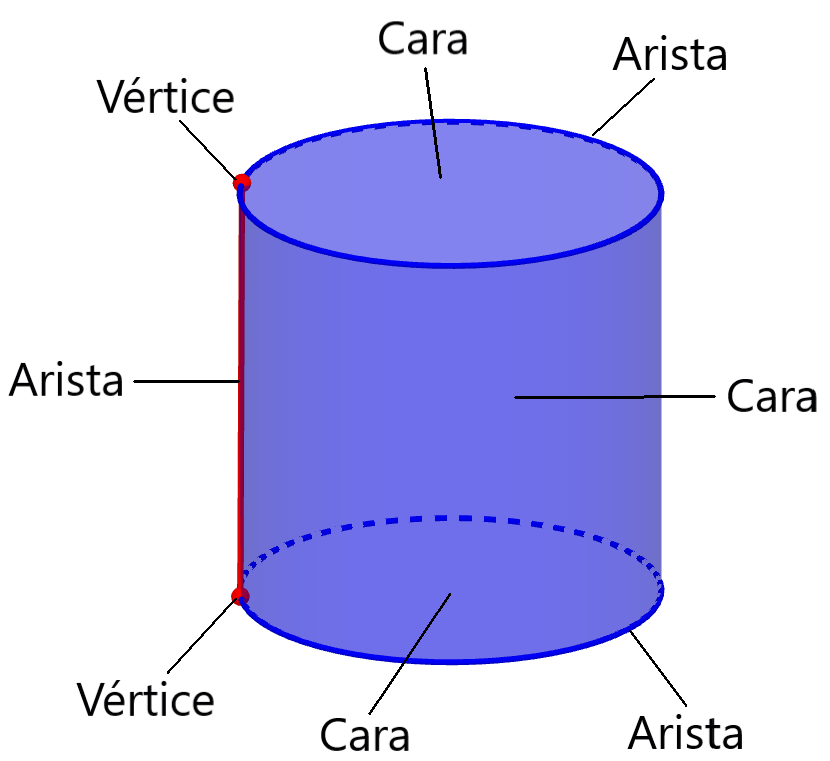
El cilindro no es un poliedro, por lo que las caras, los vértices y las aristas de los cilindros son consideradas en una manera un poco diferente a poliedros como el cubo, el prisma y otros. Sin embargo, podemos darle una estructura similar a la estructura de los poliedros, específicamente le damos una estructura CW-complejo. En resumen, un CW-complejo es similar a un poliedro, con la excepción que las caras y las aristas pueden tener curvatura. Usando esto, podemos determinar que un cilindro tiene 3 caras, 3 aristas y 2 vértices.
A continuación, conoceremos más detalles sobre las caras, los vértices y las aristas de los cilindros usando diagramas.
Caras de un cilindro
A diferencia de las caras de los poliedros, no todas las caras de los cilindros son superficies planas. Los cilindros están compuestos de tres caras, dos caras circulares que forman las bases del cilindro y una cara formada por el resto de la superficie del cubo.
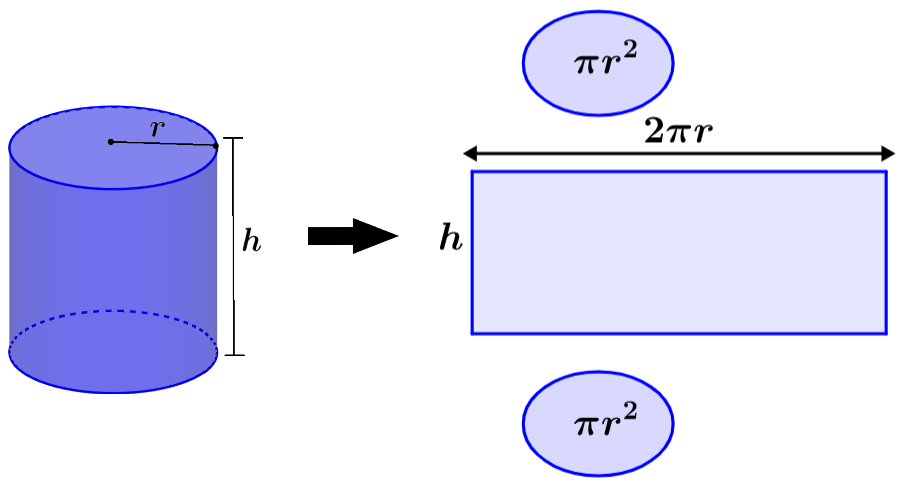
Si es que extendiéramos al cubo, la tercera cara tendría la forma de un rectángulo como se muestra en el diagrama:
Si es que sumamos las áreas de las tres caras, obtendremos el área superficial del cilindro. Sabemos que cada cara circular debe tener un área de πr², por lo que las dos bases tienen un área de 2πr². La tercera cara es formada al estirar la superficie que une a las bases.
Al estirar esta superficie, formamos un rectángulo que tiene una longitud igual a la circunferencia de las bases circulares y una altura igual a la altura del cilindro. Entonces, el área de esta superficie es 2πrh. El área superficial total es igual a 2πr²+2πrh.
Vértices de un cilindro
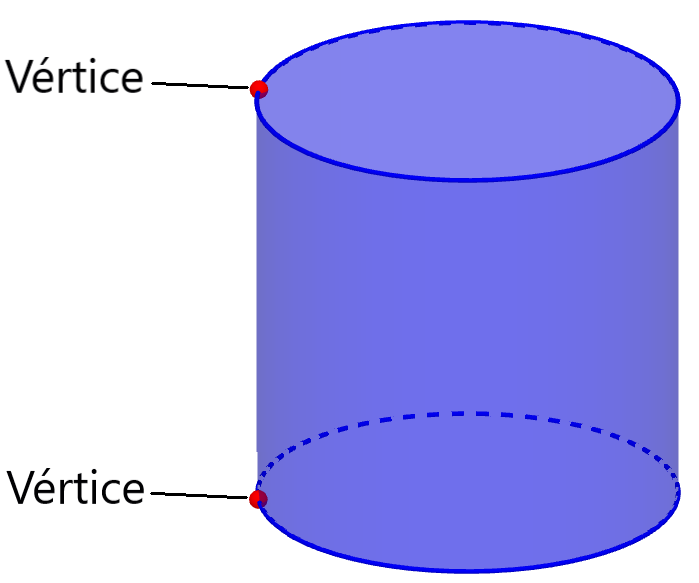
En el caso de poliedros, los vértices son los puntos en donde dos segmentos de línea se encuentran. Para los cilindros, estamos considerando la estructura CW-complejo, tal como mencionado en la introducción.
Esto nos permite tomar en cuenta a caras que tienen superficies curvadas y a aristas que también presentan una curvatura. Entonces, podemos concluir que tenemos dos vértices en un cilindro, uno en cada círculo.
Podemos interpretar a esto como el punto que marcamos cuando empezamos a trazar un círculo y en donde terminamos una vuelta completa. Además, también podemos considerar a esos puntos, como los lugares en donde se encuentra la superficie curva del cilindro.
Aristas de un cilindro
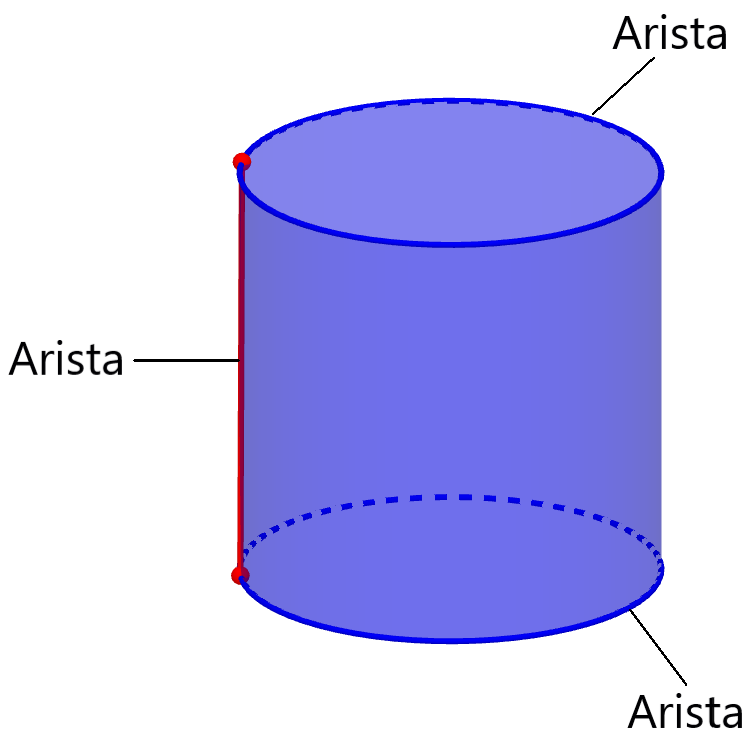
Las aristas son consideradas como segmentos de líneas en los límites de poliedros que unen a dos vértices. Sin embargo, en los cilindros tenemos dos aristas que tienen curvatura, las cuales son la circunferencia de los círculos en las bases.
Además, tenemos una tercera arista que une a los dos vértices de los círculos y que se ubica a lo largo de la cara lateral. Entonces, tenemos un total de 3 aristas.
Hemos visto que un cilindro tiene 3 caras, 2 vértices y 3 aristas. Esto cumple con la característica de Euler, la cual es un número definido que sirve para describir la forma o la estructura de poliedros o espacios topológicos.
Entonces, la característica de Euler de un cilindro es 2-3+3=2, lo cual concuerda con la característica de Euler de 2 de una esfera. Esto es correcto ya que un cilindro es homotópicamente equivalente a una esfera.
Véase también
¿Interesado en aprender más sobre cilindros? Mira estas páginas: