El ortocentro de un triángulo puede ser encontrado usando dos métodos principales. Podemos graficar las alturas del triángulo y encontrar el punto de intersección. Alternativamente, podemos encontrar las coordenadas del ortocentro algebraicamente.
En este artículo, aprenderemos cómo encontrar el ortocentro de un triángulo usando los dos métodos indicados. Luego, resolveremos algunos ejercicios de práctica.
¿Qué es el ortocentro de un triángulo?
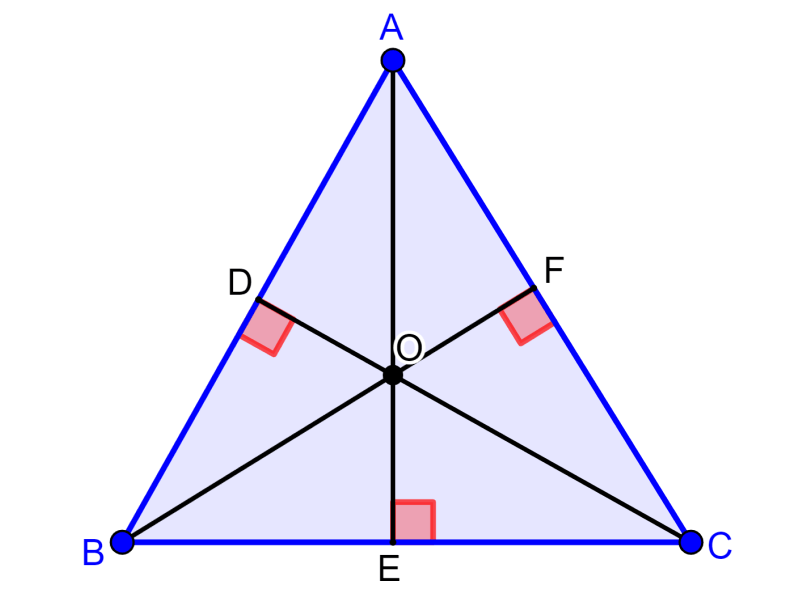
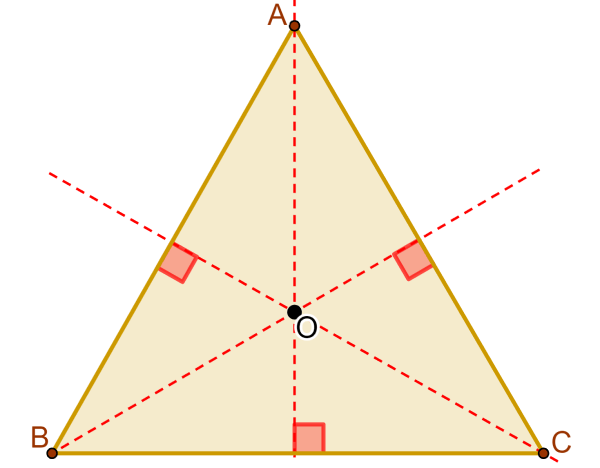
El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo. En el siguiente diagrama, podemos ver que el punto O es el ortocentro:
Recordemos que las alturas del triángulo son los segmentos perpendiculares que conectan a un vértice con su lado opuesto. Las alturas siempre forman un ángulo de 90° con el lado correspondiente.
Ortocentro de triángulos comunes
Dependiendo del tipo de triángulo que tengamos la ubicación del ortocentro varía.
Ortocentro de triángulos agudos
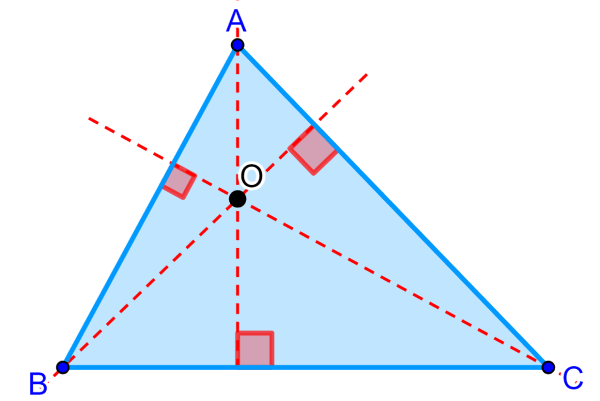
El ortocentro de todos los triángulos agudos siempre se ubica dentro del triángulo. Recuerda que un triángulo agudo se caracteriza porque todos sus ángulos internos son menores a 90°.
Ortocentro de triángulos obtusos
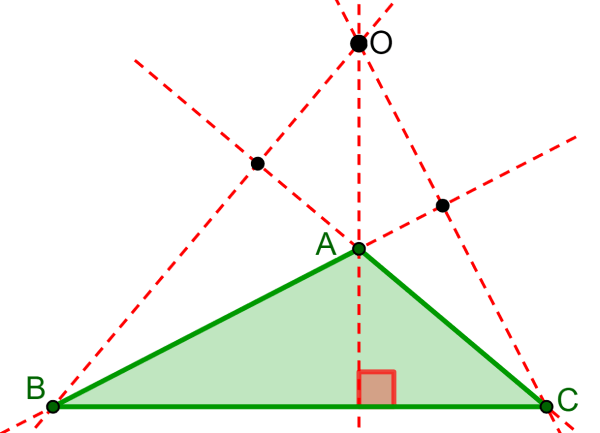
El ortocentro de todos los triángulos obtusos siempre se ubica fuera del triángulo. Recuerda que un triángulo obtuso se caracteriza por tener un ángulo mayor a 90°.
Ortocentro de triángulos rectángulos
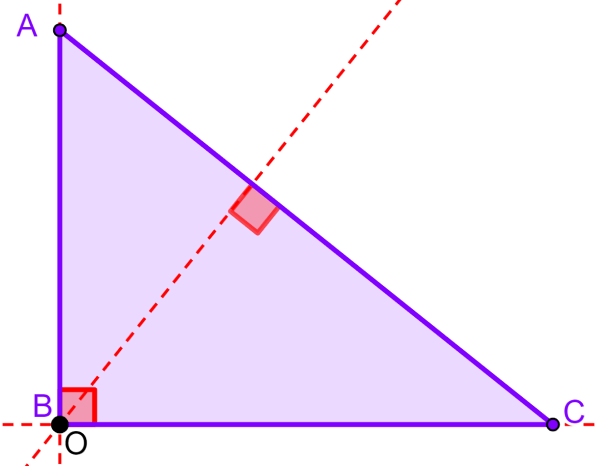
El ortocentro de todos los triángulos rectángulos se ubica en el vértice central del triángulo rectángulo. Recuerda que un triángulo rectángulo tiene un ángulo de 90°.
Ortocentro de triángulos equiláteros
El ortocentro de todos los triángulos equiláteros se ubica en la misma posición del centroide del triángulo. Recuerda que los triángulos equiláteros tienen sus tres lados con la misma longitud.
Encontrar el ortocentro de un triángulo gráficamente
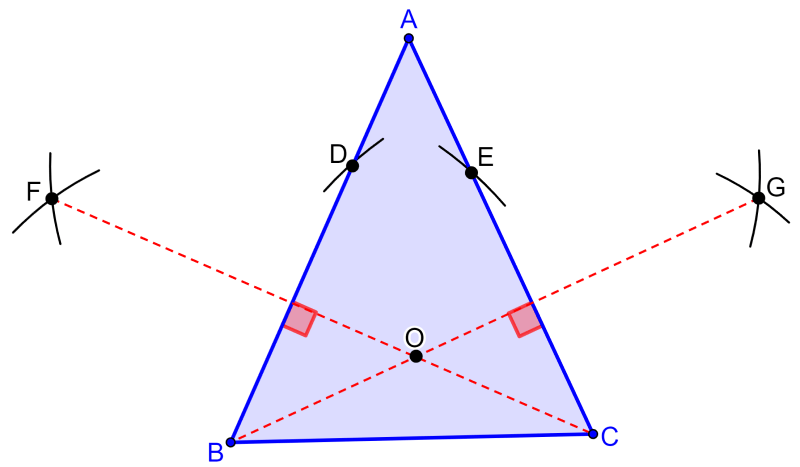
Podemos encontrar el ortocentro de un triángulo gráficamente al trazar dos alturas del triángulo y encontrar su punto de intersección.
A su vez, podemos encontrar las alturas al trazar las líneas perpendiculares desde los vértices hasta los lados opuestos. Realizamos esto con los siguientes pasos:
Paso 1: Usando un radio igual a BC y centrándonos en el punto B, trazamos un arco en el lado AC para formar el punto E.
Paso 2: Usando un radio igual a BC y centrándonos en el punto C, trazamos un arco en el lado AB para formar el punto D.
Paso 3: Usando un radio igual a BD, trazamos arcos intersecantes desde B y D para formar el punto F y trazamos el segmento CF.
Paso 4: Usando un radio igual a CE, trazamos arcos intersecantes desde C y E para formar el punto G y trazamos el segmento BG.
Paso 5: Señalamos el punto de intersección de los segmentos CF y BG.
Los segmentos CF y BG son perpendiculares a los lados AB y AC respectivamente. Esto significa que representan a las alturas del triángulo. Por lo tanto, el punto de intersección es el ortocentro del triángulo.
Encontrar el ortocentro de un triángulo algebraicamente
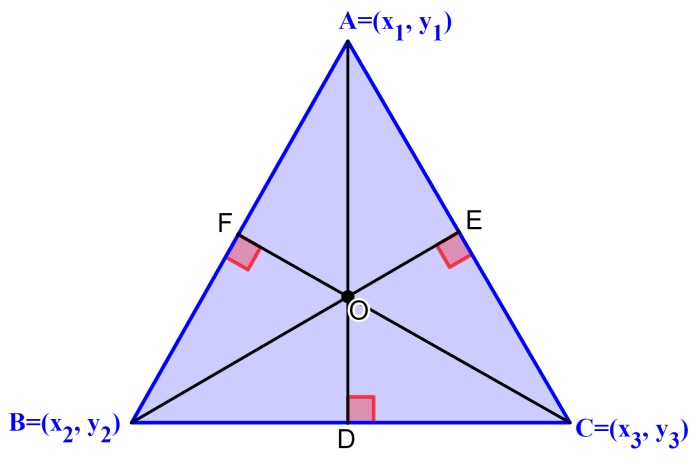
El ortocentro de un triángulo puede ser encontrado algebraicamente usando las coordenadas de los vértices del triángulo. Podemos seguir el proceso usando el siguiente triángulo.
En este triángulo, A($latex x_{1},~y_{1}$), B($latex x_{2},~y_{2}$), C($latex x_{3},~y_{3}$) son los vértices y AD, BE y CF son las alturas. El punto O es el ortocentro ya que es el punto de intersección.
Paso 1: Para encontrar las alturas, tenemos que empezar encontrando las pendientes de los lados del triángulo. Para esto, usamos la fórmula de la pendiente:
$latex m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
Representando a la pendiente de la línea AC como $latex m_{AC}$, tenemos:
$latex m_{AC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
De igual forma, también tenemos:
$latex m_{BC}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
Paso 2: Una vez que tengamos las pendientes de los lados, podemos encontrar las pendientes de las alturas considerando que las alturas son perpendiculares a los lados. La pendiente de una línea perpendicular a otra línea es:
pendiente de línea perpendicular $latex =-\frac{1}{m}$
en donde, m es la pendiente de la línea original.
Entonces, las pendientes de las alturas son:
Pendiente de BE: $latex m_{BE}=-\frac{1}{m_{AC}}$
Pendiente de AD: $latex m_{AD}=-\frac{1}{m_{BC}}$
Paso 3: Podemos encontrar las ecuaciones de las líneas que pasan por BE y AD usando la forma punto-pendiente. Entonces, tenemos:
$latex m_{BE}=\frac{y-y_{2}}{x-x_{2}}$
$latex m_{AD}=\frac{y-y_{1}}{x-x_{1}}$
Paso 4: Dado que conocemos los valores de $latex (x_{1},~y_{1})$ y $latex (x_{2},~y_{2})$, podemos usar cualquier método para resolver el sistema de ecuaciones y encontrar los valores de x y y, las cuales son las coordenadas del ortocentro.
Ejemplos resueltos del ortocentro de un triángulo
En los siguientes ejemplos, podemos ver cómo encontrar las coordenadas del ortocentro de un triángulo algebraicamente.
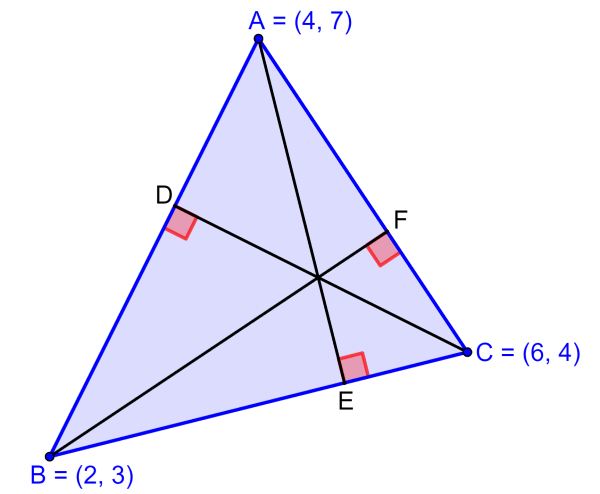
EJEMPLO 1
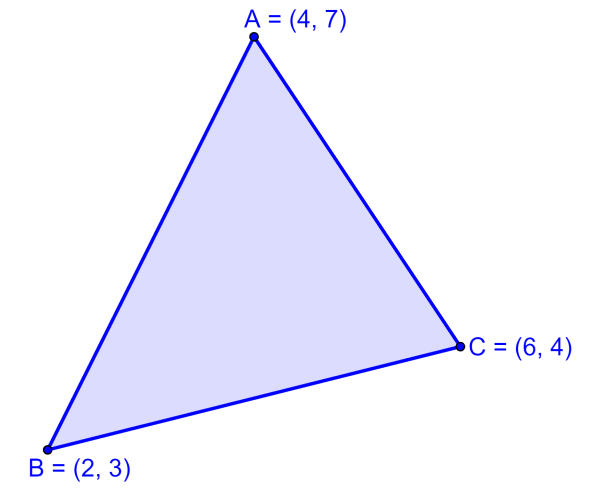
Si es que un triángulo tiene los vértices A(5, 7), B(2, 3) y C(6, 4), encuentra las pendientes de sus lados.
Solución: Tenemos las siguientes coordenadas:
- $latex (x_{1},~y_{1})=(5, ~7)$
- $latex (x_{2},~y_{2})=(2,~3)$
- $latex (x_{3},~y_{3})=(6,~4)$
Usando la fórmula de la pendiente, podemos determinar la pendiente de cada lado.
Pendiente de AC:
$latex m_{AC}=\frac{y_{3}-y_{1}}{x_{3}-x_{1}}$
$latex m_{AC}=\frac{4-7}{6-5}$
$latex m_{AC}=-3$
Pendiente de BA:
$latex m_{BA}=\frac{y_{1}-y_{2}}{x_{1}-x_{2}}$
$latex m_{BA}=\frac{7-3}{5-2}$
$latex m_{BA}=\frac{4}{3}$
Pendiente de BC:
$latex m_{BC}=\frac{y_{3}-y_{2}}{x_{3}-x_{2}}$
$latex m_{BC}=\frac{4-3}{6-2}$
$latex m_{BC}=\frac{1}{4}$
EJEMPLO 2
Usa las pendientes encontradas en el Ejemplo 1, para determinar las coordenadas del ortocentro del triángulo.
Solución: Tenemos que encontrar las pendientes de las líneas perpendiculares a los lados ya que corresponden a las alturas del triángulo. Entonces, tenemos:
- $latex m_{AE}=$ perpendicular a BC
- $latex m_{BF}=$ perpendicular a AC
- $latex m_{CD}=$ perpendicular a AB
La pendiente de una línea perpendicular es igual a $latex -\frac{1}{m}$, en donde, m es la pendiente de la línea original, tenemos:
$latex m_{AE}=-4$
$latex m_{BF}=\frac{1}{3}$
$latex m_{CD}=-\frac{3}{4}$
Usando la forma punto-pendiente, $latex y-y_{1}=m(x-x_{1})$, podemos encontrar las ecuaciones de las líneas perpendiculares. Solo necesitamos dos ecuaciones para encontrar el punto de intersección.
Usamos la pendiente de CD y el punto C=(6, 4) para encontrar la primera ecuación:
$latex y-4=-\frac{3}{4}(x-6)$
$latex 4(y-4)=-3(x-6)$
$latex 4y-16=-3x+18$
$latex 3x+4y=34$
Ahora, usamos la pendiente de BF y el punto B=(2, 3) para encontrar la segunda ecuación:
$latex y-3=\frac{1}{3}(x-2)$
$latex 3(y-3)=x-2$
$latex 3y-9=x-2$
$latex -x+3y=7$
Cualquier método puede ser usado para resolver el sistema de dos ecuaciones y encontramos la solución $latex x=\frac{74}{18},~ y=\frac{55}{13}$.
Esta solución representa al punto de intersección de las líneas. Por lo tanto, las coordenadas del ortocentro son $latex (\frac{74}{18},~\frac{55}{13})$.
Ejercicios para resolver del ortocentro de un triángulo
Resuelve los siguientes ejercicios usando el método algebraico para encontrar las coordenadas del ortocentro.
Véase también
¿Interesado en aprender más sobre centroide, incentro, ortocentro y circuncentro de un triángulo? Mira estas páginas:
Jefferson Huera Guzmán
Jefferson es el autor principal y administrador de Neurochispas.com. Los contenidos interactivos de Matemáticas y Física que he creado han ayudado a muchos estudiantes.
